钢筋混凝土梁抗剪承载力的FASTM显式计算方法
2020-11-10赵盈江毛科强张恒伟
赵盈江,毛科强,张恒伟,陈 旦
(1.云南建投博昕工程建设中心试验有限公司,云南 昆明 650206;2.重庆交通大学 土木工程学院,重庆 400074)
钢筋混凝土(RC)梁的抗剪承载力研究开始于19世纪末,一百多年来国内外研究人员进行了数以千计的混凝土构件剪切试验,并提出了多种剪切失效机理及计算模型。目前,RC梁的抗剪承载力理论主要包括修正压力场理论、扰动压力场理论、固定倾角软化桁架理论(FASTM)和变角桁架理论(RASTM)等。修正压力场理论和扰动压力场理论认为混凝土构件的抗剪承载力由混凝土贡献和钢筋贡献两部分组成,它们将钢筋混凝土看做是一种新的正交异性材料,通过联立平面剪切问题中平衡方程、协调方程和物理方程,引入斜裂缝间混凝土的拉伸硬化,并通过考察裂缝处的应力局部平衡来限制混凝土中拉应力。固定倾角软化桁架理论和变角桁架理论也是将钢筋混凝土看做一种材料,与压力场理论不同之处在于:一是取消了裂缝处局部平衡的检查;二是将钢筋看做为“混凝土包裹的钢筋”,不再使用裸筋的应力-应变关系,而是使用混凝土包裹下钢筋的应力-应变关系。潘钻峰等[1]结合209片钢筋混凝土矩形梁的剪切试验数据库提出了基于MCFT的抗剪承载力显式计算方法,但计算结果高估了RC梁的抗剪承载力,偏不安全。季韬等[2]在固定倾角软化桁架模型的基础上提出了随动倾角软化桁架模型,计算结果与试验值更加吻合,求解过程更为繁琐,不利于工程推广应用。魏巍巍等[3]建立了临界裂缝倾角与配箍率、箍筋屈服强度、纵筋应变、截面有效高度等参数之间的经验关系模型,但是仅适用于HPB235和HRB335钢筋。张南等[4]在试验的基础上,考虑混凝土斜压杆的软化效应,推导了桁架模型承载力公式,计算结果与试验值符合较好。Rahal[5]通过简化修正压力场理论得到SMCS方法,用于平面内剪切和法向应力联合作用下的膜单元失效模式的设计、计算和识别,简化结果与试验值吻合较好。王景全等[6]考虑尺寸效应、通过极限平衡法,得到有腹筋和无腹筋钢筋混凝土梁抗剪承载力统一计算公式,该公式形式简单,物理意义明确。
尽管修正压力场理论的可靠性和准确性已经得到验证,但不能准确计算高配箍率或低配箍率条件下构件的抗剪承载力,裂缝处局部平衡检查时算法收敛条件苛刻,裂缝剪切应力检验很难有效执行,而固定角软化桁架模型虽然取消了裂缝处局部平衡的检查,但材料复杂的本构关系导致算法迭代过程更为复杂,不便于工程推广应用。本文基于FASTM理论,利用245片钢筋混凝土梁的试验数据,引入具有显著统计意义的回归关系,提出RC梁抗剪承载力的显式计算方法。
1 FASTM模型简介
1985年Thomas将钢筋混凝土的平衡条件、应变协调条件和材料应力应变关系结合起来建立的FASTM理论认为受剪构件的受力变形行为由13个主导方程控制,包括3个静力平衡方程(式(1)~(3))、7个变形协调方程 (式(4)~(10))、3个钢筋和混凝土应力-应变本构方程(式(11)~(13))。这13个主导方程包含15个变量,其中包含8个与力的作用相关的变量σl,σt,τl t,fl,ft,σ1,σ2,τ21,6个与变形相关的变量εl,εt,γl t,ε1,ε2,γ21,1个独立变量ζ[1]。
σl=σ2cos2α+σ1sin2α+τ21sin2α+ρlfl
(1)
σt=σ2sin2α+σ1cos2α-τ21sin2α+ρtft
(2)
τl t=(σ1-σ2)sinαcosα+τ21cos2α
(3)
εl=ε2cos2α+ε1sin2α+0.5γ21sin2α
(4)
εt=ε2sin2α+ε1cos2α-0.5γ21sin2α
(5)
γl t/2=(ε1-ε2)sinαcosα+0.5γ21cos2α
(6)
γ21=-0.85ε1(1-η)
(7)
γ21=(εl-εt)csc2α+(ε1-ε2)cot2α
(8)
τ21=τ21m[1-(1-γ21/γ210)6]
(9)
τ21=[ρlfl-ρtft-(σ2-σ1)cot2α]/(2sin2α)
(10)
(11)
(12)
(13)
式中:σl,σt,τl t分别为l-t坐标系(外荷载坐标系)中钢筋混凝土单元的平均正应力和剪应力;σ1,σ2,τ21分别为2-1坐标系(主应力坐标系)中混凝土单元的平均正应力和剪应力;α为l-t标系和2-1坐标系的夹角,定义为固定角,取45°;fl,ft分别为l和t方向的平均钢筋应力;ρl,ρt分别为l和t方向的钢筋配筋率;fly,fty分别为l和t方向的钢筋屈服强度(裸钢);εl,εt,γl t分别为l-t坐标系中钢筋混凝土单元的平均正应变和剪应变;ε1,ε2,γ21分别为2-1坐标系中混凝土单元的平均正应变和剪应变;η为钢筋混凝土单元双向配筋不均匀系数;ζ为受压混凝土软化系数;f′c为混凝土圆柱体抗压强度;ε0为混凝土单轴受压时峰值应力对应的应变,一般取-0.002;fcr为混凝土开裂应力;εcr为混凝土开裂应变,一般取0.00008;Ec,Es分别为混凝土弹性模量和钢筋弹性模量;fy,fn分别为钢筋的屈服强度(裸钢)和埋置在混凝土中的钢筋屈服强度;εy,εn分别为钢筋的屈服应变(裸钢)和埋置在混凝土中的钢筋屈服应变;τ21m,γ210分别为混凝土开裂时的最大剪应力和最大剪应变。其中式(7)和式(9)通过大量试验研究回归分析得到。
由于未知数个数多于主导控制方程个数,应用时需要假定某一变量,然后通过迭代方式完成方程求解,具体步骤可参考文献[1]。得到τl t-γl t曲线后,在忽略受压区混凝土对构件抗剪承载力贡献的情况下,矩形截面梁抗剪承载力V可表示为:
V=bh0τl t_max
(14)
式中:b为矩形截面宽度;h0为截面有效高度;τl t_max为τl t-γl t曲线中τl t的最大值。
2 矩形截面梁抗剪承载力试验
研究钢筋混凝土梁抗剪承载力的理论计算模型必须有样本容量较大的试验梁数据库作为支撑。本文通过收集公开发表的期刊论文上的试验数据[7~16],得到245片集中荷载作用下有腹筋钢筋混凝土矩形截面简支梁的抗剪承载力试验结果。245片矩形截面试验梁截面宽度b=80~457 mm;有效高度h0=140~1925 mm;剪跨比λ=1.0~5.0;混凝土棱柱体抗压强度f′c=13.76~116.56 MPa;纵筋配筋率ρz=0.36%~ 6.96%;箍筋配筋率ρk=0.057%~1.810%;纵筋屈服强度fzy=302~1068 MPa;箍筋屈服强度fky=215~820 MPa。
使用FATSTM抗剪承载力“两阶段”迭代计算方法计算得到245片梁的抗剪承载力,为方便计算结果的讨论,以RC梁的抗剪承载力试验结果Vtest为参照对计算结果Vcal进行无量纲归一化处理(Vcal/Vtest),结果如图1所示。另外,为了定量评价FASTM迭代算法的正确性,图1还给出了基于GB 50010-2010《混凝土设计规范》的计算结果(VGB/Vtest)以及基于JTG D62-2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》的计算结果(VJTG/Vtest)作为对比。从图1中不难发现:(1)从均值上看,FASTM模型计算结果与试验值之比为1.03,而规范GB 50010-2010和JTG D62-2004承载力计算值仅为试验值的80%和72%,这证明了FASTM模型迭代算法能较好地预测矩形截面梁的抗剪承载力;(2)从离散性上看,三种方法计算得到的245片RC矩形梁的归一化抗剪承载力的变异系数均超过0.15。
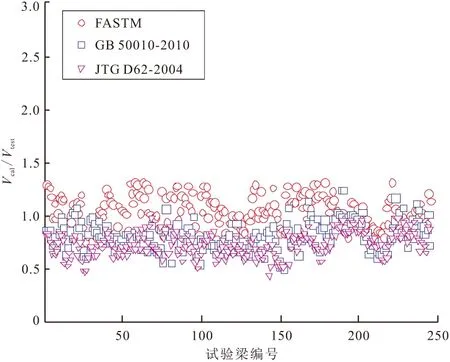
图1 245片钢筋混凝土梁抗剪承载力试验值和计算值
3 基于FASTM的RC梁抗剪承载力显式计算方法
FASTM模型虽然能较为准确地预测RC梁的抗剪承载力,但材料本构关系是分段函数,计算过程也需要复杂的迭代运算,不便于工程推广。为简化分析过程,拟通过分析FASTM迭代计算过程中某些中间变量的统计关系,引入具有显著统计意义的关系作为附加控制方程,联立平衡方程、协调方程、本构方程实现抗剪承载力的显式计算。
3.1 RC梁抗剪极限状态下纵筋、箍筋、混凝土的受力状态
为考察矩形截面RC梁达到抗剪极限状态时纵筋、箍筋、混凝土的受力行为,图2给出了达到抗剪承载力极限状态时245片试验梁的四项无量纲指标:(1)箍筋应变εk与箍筋屈服应变εnk之比εk/εnk;(2)纵筋应变εz与纵筋屈服应变εnz之比εz/εnz;(3)混凝土拉应变ε1与开裂应变εcr之比ε1/εcr;(4)混凝土压应变ε2与考虑软化系数的峰值应力所对应的应变ζε0之比ε2/ζε0。
从图2可以发现:RC矩形梁达到抗剪极限状态时,245片试验梁的箍筋均发生屈服,而绝大多数梁的纵筋未屈服,表明本文遴选的245片试验梁的破坏形态绝大多数是典型的剪切破坏,这可能也是FASTM理论的抗剪承载力计算值与试验值吻合较好的原因,当梁体发生斜拉破坏或斜压破坏时,梁体破坏模式与FASTM理论的假设相差较多,FASTM理论的预测结果可能会失真;混凝土主拉应变均超过开裂应变,而绝大多数梁体混凝土主压应变则超过峰值应力对应的应变,需考虑混凝土的软化效应。
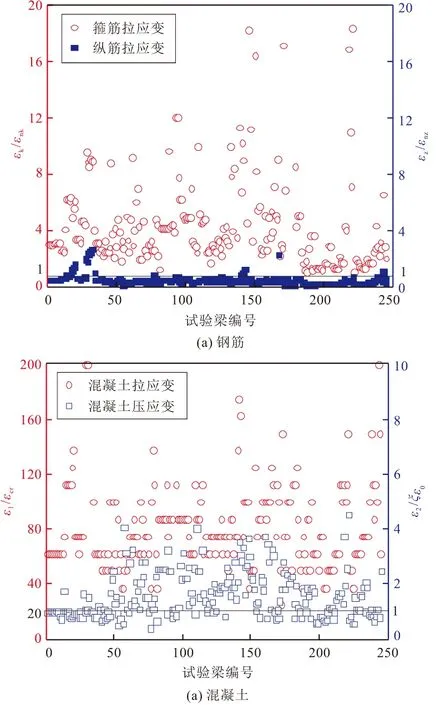
图2 RC梁抗剪承载力极限状态下钢筋和混凝土受力特征
为从统计学角度考察4组变量的特征,利用单边 t 检验方法分析 4 组变量是否显著小于 1 或者显著大于1,检验水准α取0.05时结果如表1所示,从中可以发现:(1)箍筋应变εk与箍筋屈服应变εnk之比εk/εnk、混凝土拉应变ε1与开裂应变εcr之比ε1/εcr、混凝土压应变ε2与考虑软化系数的峰值应力所对应的应变ζε0之比ε2/ζε0这3组变量各自的检验统计量值均显著大于自由度为244的t分布0.005分位数t0.005(244),表明该三个变量在统计意义上显著大于1;(2)纵筋拉应变εz与纵筋屈服应变εnz之比εz/εnz的检验统计量值小于自由度为244的t分布0.005分位数t0.005(244),表明εz/εnz在统计意义上显著小于1。
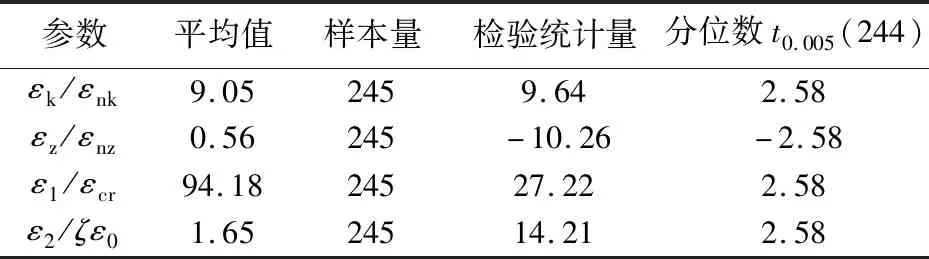
表1 抗剪承载力极限状态下钢筋、混凝土力学特性的t检验结果
因此,从统计学角度可以定量且合理地将箍筋、纵筋和混凝土主拉应变和压应变分段表达的本构关系简化为单一函数,这为本文的显式计算方法分析提供了便利。
3.2 RC梁抗剪极限状态下附加控制方程
为寻找RC梁抗剪承载力极限状态时箍筋应变εk、纵筋应变εz、混凝土主拉应变ε1、混凝土主压应变ε2、混凝土剪应变γ21之间的统计关系,利用非参数皮尔逊相关性检验方法分析上述5组变量之间的相关性,结果如表 2所示。
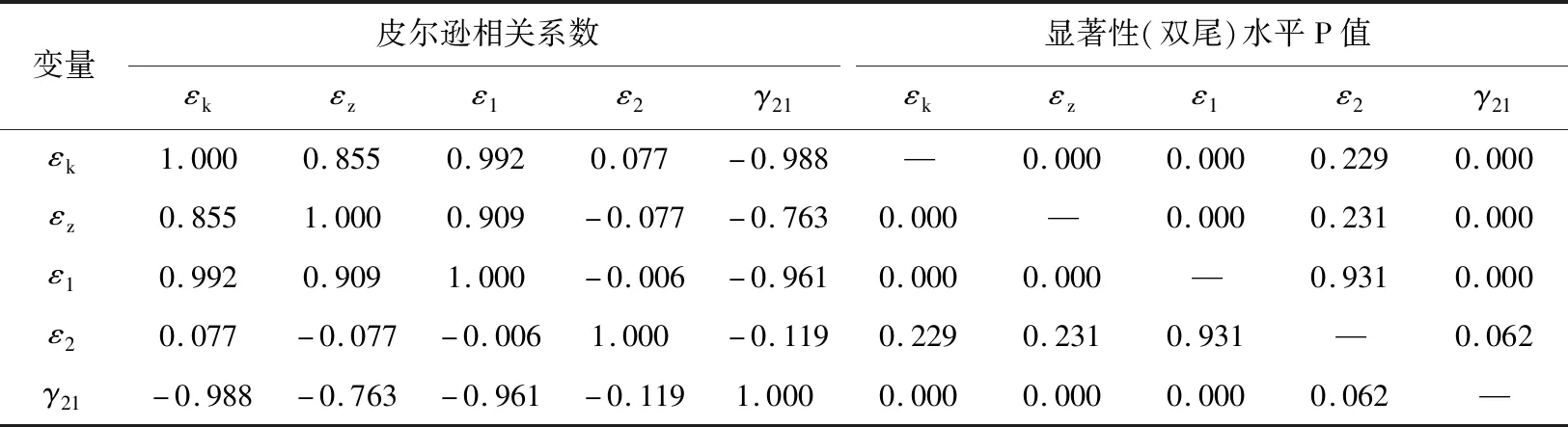
表2 抗剪承载力极限状态下钢筋、混凝土力学特性的相关性检验结果
从中可以发现:在抗剪极限状态下,245片样本试验梁的箍筋应变εk与混凝土拉应变ε1、混凝土剪应变γ21之间存在极为显著的相关关系(皮尔逊相关系数超过0.90,显著性水平P值小于0.01);纵筋应变εz与箍筋应变εk、混凝土主拉应变ε1之间也存在显著的相关关系(皮尔逊相关系数超过0.80,显著性水平P值小于0.01);其他变量之间相关性并不显著。
图3给出了245片试验梁的混凝土剪应变与箍筋拉应变之比β1=γ21/εk、箍筋拉应变与混凝土拉应变之比β2=εk/ε1的计算值,从中可以看出尽管245片试验梁的混凝土强度、纵筋和箍筋的配筋率、跨径不尽相同,但达到抗剪极限状态时β1和β2的离散性并不大。β1的均值为-0.72,变异系数仅-0.05;β2的均值为0.78,变异系数仅0.06。而文献[7]通过试验得到β1和β2的均值分别为-0.71和0.75,与本文的统计结果较为接近,两组如此显著的回归关系将为FASTM模型的显式计算提供可能。
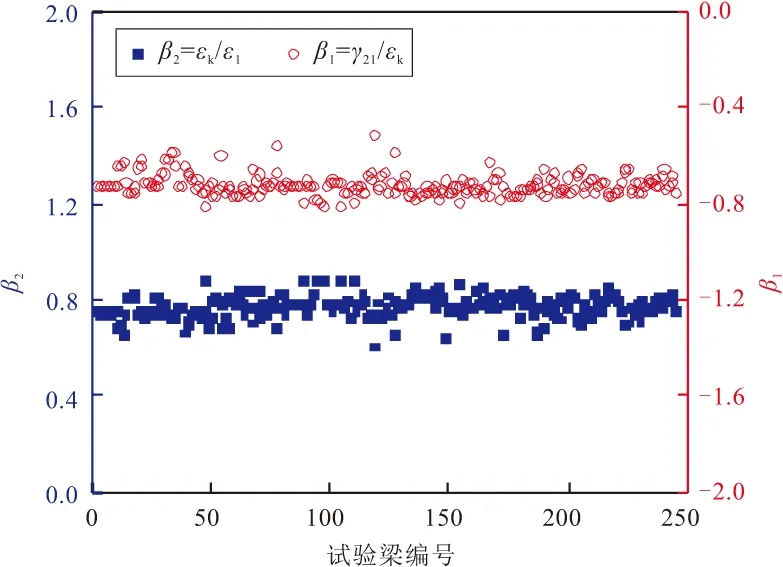
图3 245组试验梁的β1和β2
3.3 FASTM显式计算方法
通过统计分析245片钢筋混凝土矩形梁在抗剪承载力极限状态条件下纵筋、箍筋和混凝土的力学行为,发现245片梁在抗剪承载力极限状态下梁内箍筋均发生屈服且混凝土主拉应变均超过其开裂应变,绝大部分梁体的纵筋未屈服且混凝土主压应变也超过峰值应力对应的应变,据此当仅关心钢筋混凝土梁体抗剪承载力时,可作出以下4种假定,实现对箍筋、纵筋和混凝土应力的本构关系的简化。
(1)结合式(7),假定钢筋混凝土梁达到抗剪承载力极限状态时,混凝土平均拉应力-应变曲线为开裂应变后的曲线:
σ1=fcr(εcr/ε1)0.4
(15)
(2)结合式(8),假定钢筋混凝土梁达到抗剪承载力极限状态时,混凝土平均压应力-应变曲线为达到峰值应力后的曲线:
(16)
(3)结合式(10),假定钢筋混凝土梁达到抗剪承载力极限状态时,箍筋应力-应变曲线为屈服后的曲线:
(17)
(4)结合式(10),假定钢筋混凝土梁达到抗剪承载力极限状态时,纵筋应力-应变曲线为屈服前的曲线:
fz=Esεz
(18)
另外,鉴于245片试验梁在达到抗剪承载力极限状态时,混凝土剪应变与箍筋拉应变、箍筋拉应变与混凝土拉应变均有极为显著的相关关系,且β1和β2的变异系数较小,因此可以考虑将式(18)(19)作为附加控制方程引入FASTM算法内。
γ21=β1εk=-0.72εk
(19)
εk=β2ε1=0.78ε1
(20)
将式(15)~ (20)带入平衡方程,即可建立仅含混凝土拉应变εl的平衡方程,利用数值算法求解得到εl后,带入平衡方程,即可方便地得到开裂混凝土最大剪应力τl t max。
(21)
求得最大剪应力τl t max后,带入式(13)即可求得RC梁抗剪承载力极限值V:
(22)
4 基于FASTM显式计算方法的RC梁承载力预测
4.1 计算结果分析
利用式(22)计算245片试验梁的抗剪承载力,为方便计算结果的讨论,以RC梁的抗剪承载力试验结果Vtest为参照对计算结果Vcal进行无量纲归一化处理(Vcal/Vtest),结果如图4所示。
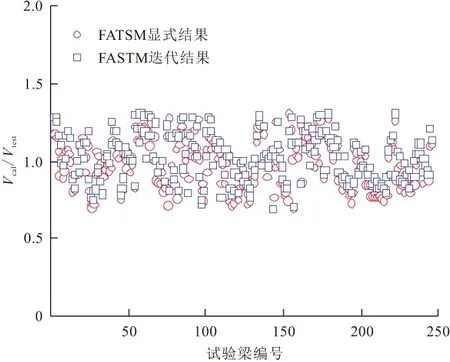
图4 显式算法的正确性验证
从图4可以看出:基于FASTM显式计算方法得到的RC梁抗剪承载力与试验值吻合良好,但略大于迭代计算结果,这表明RC梁抗剪极限状态下,对钢筋和混凝土本构方程的简化处理以及附加方程的引入并未显著增加计算结果的离散性和计算误差,显式算法计算结果偏大的原因可能是由于显式算法对材料本构关系的简化处理造成的(特别是抗剪承载力极限状态下混凝土主压应变均超过其峰值应变的假定),因为图2b中不难发现抗剪承载力极限状态下245片试验梁的混凝土主压应变有不少仍低于其峰值应力对应的压应变。
4.2 剪跨比的影响
FASTM理论是基于危险截面上微元体的应力平衡条件推导的,无法考虑剪跨比λ对混凝土梁体抗剪承载力的影响,因此FASTM理论预测值可能与试验值有很大的偏差,从图4中也不难发现确实有部分梁体的Vcal/Vtest小于0.5或大于1.5。严格来说,FASTM的假定决定了其仅能相对准确地预测破坏模式为剪压破坏的钢筋混凝土梁体的抗剪承载力,由于剪跨比是影响钢筋混凝土剪切破坏模式的主要因素,因此有必要从剪跨比方面讨论FASTM模型的适用性,为此将245片试验梁按照如表3所示的8组剪跨比范围进行分类,分别计算每个剪跨比区间内梁体抗剪承载力的FASTM预测结果。
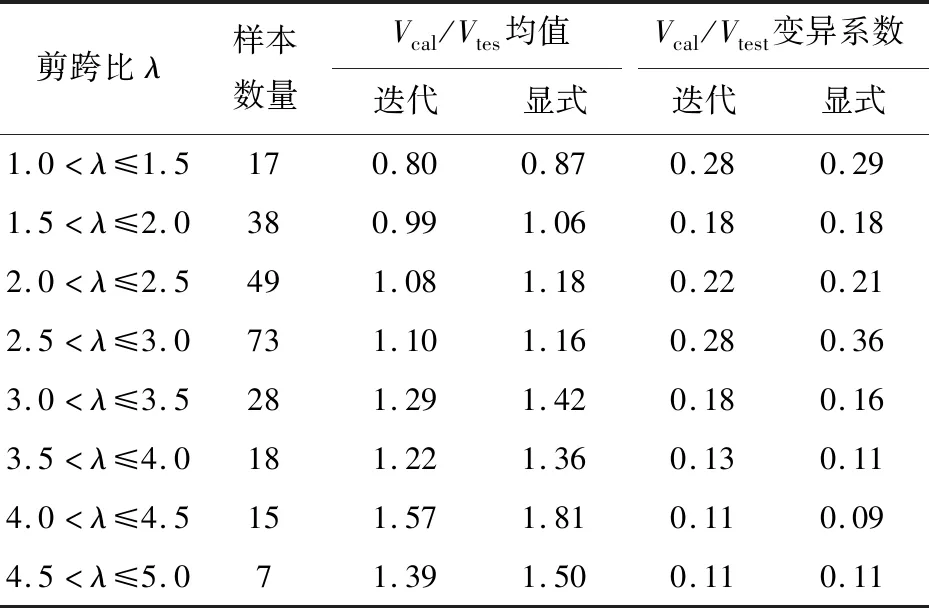
表3 不同剪跨比下FASTM模型计算结果
从表3可以发现:(1)从均值上看,FASTM的理论预测结果确实会受剪跨比影响,当剪跨比较小时,FASTM理论预测结果偏小,而当剪跨比超过3.0后理论预测结果又明显偏大;当1.5<λ≤3.0时,梁体破坏形式为典型的剪压破坏,FASTM显式算法和迭代算法计算结果误差在10%以内,且与试验值的误差也在±18%以内;(2)从离散性上看,剪跨比对FASTM理论预测值的变异系数影响不大。
5 结 论
本文基于FASTM理论,通过分析245片试验梁抗剪承载力极限状态时钢筋和混凝土受力行为的统计特征,引入具有显著统计意义的回归关系,提出了基于FASTM理论的RC梁抗剪承载力显式算法,并得到以下结论:
(1)抗剪承载力极限状态下245片试验梁箍筋均发生屈服,混凝土主拉应变均超过开裂应变,混凝土主压应变均大于峰值应力对应的应变,虽然有少许试验梁的纵筋应变大于其屈服应变,但在统计意义上纵筋应变显著小于其屈服应变,且混凝土剪应变与箍筋拉应变、箍筋拉应变与混凝土拉应变之间均有极为显著的相关关系;
(2)对抗剪承载力极限状态下钢筋和混凝土本构关系进行适当简化,并引入2个附加控制方程后即可实现对钢筋混凝土梁抗剪承载力的FASTM显式计算,且显式计算结果与试验值吻合较好;
(3)FASTM的抗剪承载力理论预测结果确实会受剪跨比影响,当剪跨比较小时,FASTM理论预测结果偏小,而当剪跨比超过3.0后理论预测结果又明显偏大;当1.5<λ≤3.0时,梁体破坏形式为典型的剪压破坏,FASTM显式算法能较为准确地计算梁体的抗剪承载力。
