X、Y状裂隙对堆积体降雨入渗的差异性影响研究

2020-11-10钱昭宇涂国祥赵石力

水力发电 2020年8期

钱昭宇，涂国祥，赵石力，李明

(1.成都理工大学，四川成都 610059；2.地质灾害防治与地质环境保护国家重点实验室，四川成都 610059)

0 引言

诱发地质灾害的因素众多，但降雨仍为主要诱发因素。据薛凯喜[1]等统计表明，中国近10年90%地质灾害都是由降雨直接或间接引起，滑坡发生率占50%以上。雨水入渗会让岩土体经历一个非饱和到饱和的过程，期间形成暂态渗流场，导致体积含水率和孔隙水压力上升，具有软化作用并造成结构损伤，并使土体容重增加，造成边坡剪应力增大，抗剪强度减少，基质吸力也相应降低，对边坡的稳定性产生重要影响[2-7]。史振宁[8]、宿文姬[9]、王一兆[10]等通过数值模拟总结出坡体含水率随降雨历时的分布变化规律，得到降雨强度和时间对雨水入渗深度和边坡稳定性的影响程度，并对相应渗透系数和孔隙水压力变化对坡体浅层滑动面的影响规律进行了探究。但在众多滑坡类型中，堆积体滑坡因其大孔隙性、强渗透性、各向异变性，所占比例一直居高不下[11-12]，并且堆积体内裂隙或局部富集粗颗粒的大孔隙常常可见，其渗透特性与周围土体具有明显差别，为雨水的差异化入渗提供了优势路径[13-15]。涂国祥[16]等以云南某滑坡为研究对象发现，降雨入渗在局部堆积的碎石土内形成高孔压，造成高水力传导率，对雨水的“快渗入，深渗透”起着关键作用。许多研究人员基于非饱和渗流理论并建立相应的数值模型，分别就堆积体内裂隙的长度、宽度、数量[17-18]、深度、位置、角度[19-20]等概化特征展开定量研究，为边坡稳定性与裂隙中雨水入渗过程的紧密相关性提供了有利的论据。

然而，滑坡堆积体裂隙种类众多，发育程度各异，相应的性质也存在较大差别，目前，关于裂隙具体展布形态对降雨入渗影响的物理试验研究还相对欠缺。笔者实地调查发现，某巨型古滑坡堆积体上裂隙多样且广泛分布，不仅弱化了堆积体结构，还形成了雨水优势流的天然通道，为古滑坡的复活演化提供了重要的外部因素。为此，本文针对该堆积体中典型发育的X、Y状裂隙(见图1)开展较为深入的室内物理模型试验，分析了X、Y状裂隙在降雨作用下渗流特性及入渗阶段的差异，并对其运移规律和影响机理进行了探讨。

图1 X、Y状裂隙

1 研究区域裂隙概况

滑坡堆积体位于澜沧江流域上游的左岸，高程为2 700～3 200 m，平均坡度为30° ，前后缘相对于中部平台较陡，整体形态似倒“V”字形。古滑坡边界见图2。据笔者现场调查，90%的坡表裂隙延伸长度为10～60 m，裂隙内有碎块石充填，胶结程度差，且周围临近裂隙发育处常伴随土体垮塌，形成高低错台、陡坎。据不完全统计，裂隙发育数量在百条以上，主要以剪切裂隙和张拉裂隙为主，坡体中部的裂隙发育数量不及前后缘，但裂隙发育范围遍布整个研究区域，且各种成因的大小裂隙常以交汇形态出现，其中形态类似X、Y状裂隙尤为典型。

相关气象资料显示，该地区历来少雨，而在2012年10月下旬连续暴雨，降雨总量达到350 mm。该滑坡堆积体在此次降雨入渗后发生强烈蠕动，加之堆积层内水分蒸发不均，导致土粒重新分离和结合，促使局部垮塌和新裂隙产生，原有裂隙也进一步发育，对土体完整性造成二次破坏，加速其结构的劣化。为具体探明坡体局部变形程度，对后缘位置的2个平硐(PD2003和PD2004，相对高差约100 m)调查发现，2个平硐(深度分别为47～58 m、61～76 m处)滑带土相对于周围堆积层明显湿润，并且局部有少量渗水，说明已经有水分从广泛发育的裂隙渗入到滑坡堆积体深部，古滑坡局部已经出现了复活演化迹象。

2 试验设计

2.1 试验装置

(1)室内模型箱。模型箱体长1.5 m、宽0.9 m、高1.2 m，由透明有机玻璃和定制角钢拼装而成，间距10 cm正方形网格划分表面，底板为不透水钢板。

(2)降雨模拟系统。由固定钢架、降雨喷头、流量表和压力表构成。降雨强度可通过供水压力与流量进行调节，控制范围15～20 mm/h。

(3)监测与数据采集仪器。①体积含水率。EC-5传感器和Em50数采仪。②基质吸力。Campbell-257传感器和CR1000数采仪。③孔隙水压力。HC-25传感器和HCSC-16数采仪。

2.2 试验方案

2.2.1试验土指标

本试验用土取样于研究区域的堆积体前缘，主要为粘土质砾石土，砾石磨圆度差，风化程度一般，泥质胶结程度均较好。为较好反映野外堆积体的降雨入渗现象，在现场从上到下，选取4个取样点(①～④)并进行初步颗分，分为8个粒组，颗粒分析见图3。试验时对超径粒(200～80 mm)进行等量替代处理，对比粒径累计曲线见图4。在土工试验制备土样时，按照土体天然密度、天然含水率均值进行配比。土样物理力学指标见表1。

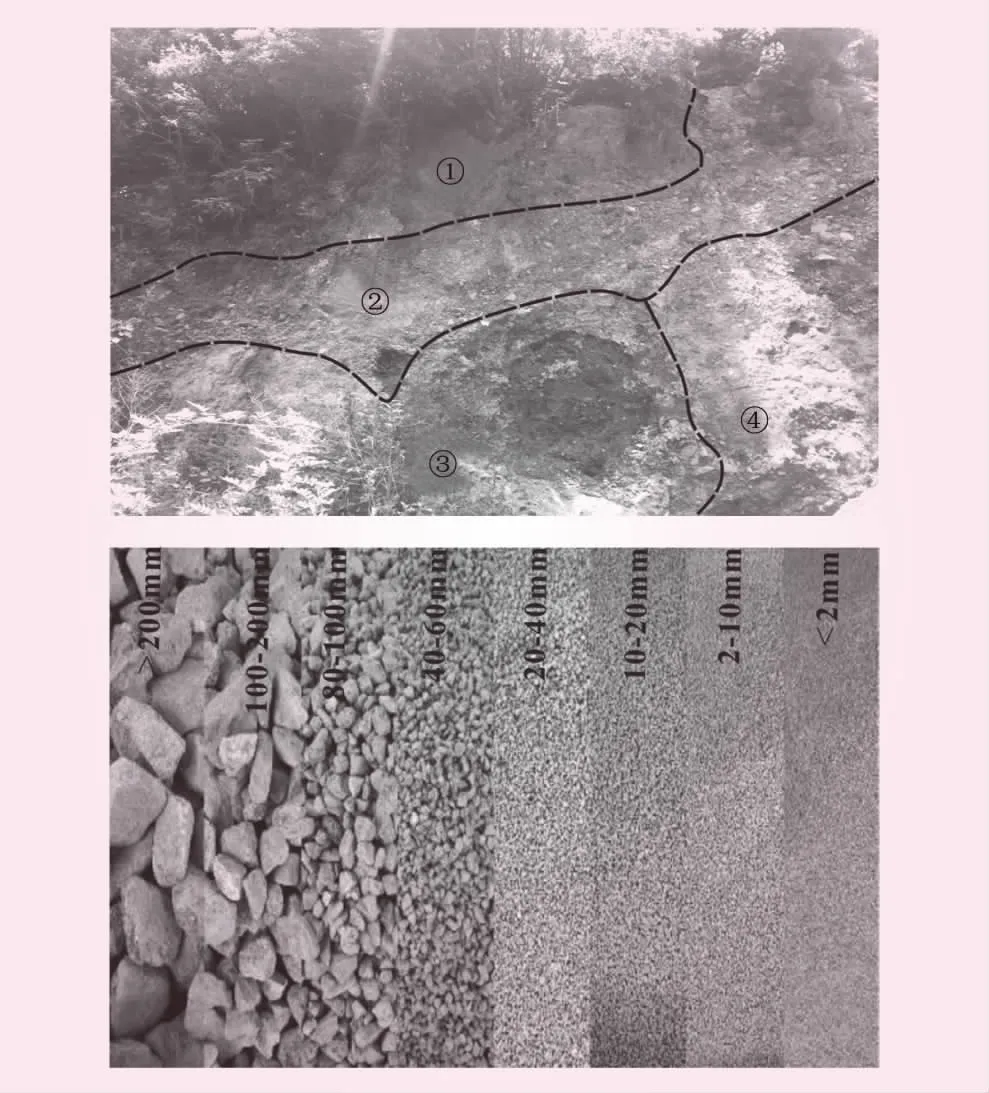
图3 野外颗粒分析

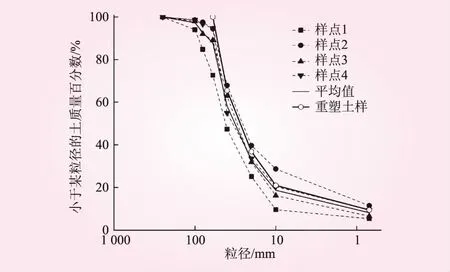
图4 粒径累计

表1 土样物理力学指标

图5 X、Y状裂隙试验设计(单位：cm)

2.2.2模型设置及降雨方案

根据研究目的，设计X、Y状2种裂隙堆积体试验，试验设计见图5。坡体堆筑以10 cm为界分层压实(共8层)，压实程度以土样天然容重19 kN/m3为标准。传感器放入预埋的PVC管中，逐层压实后，将PVC管抽离土体。堆筑完成后，模型静置6 h。为减少边界效应，在土坡表面周围涂抹一圈防水涂料。裂隙布设位置均在坡顶(隙口碎石为防变形)，为模拟野外情况，2种裂隙底部均未贯通，展布形态特征为唯一变量，其他试验条件相同，3种监测仪器各6个，编号从坡顶至坡脚位置分别为1～6号(体积含水率为W1～W6，孔隙水压力为P1～P6，基质吸力为M1～M6)。X、Y状裂隙堆积体模型见图6。试验共2组，每组进行4轮间歇性降雨，每轮时长为1 h，起始时间为10∶00，持续降雨1 h后停止，观察并监测其入渗过程至湿润锋触底为止。经实际测算，降雨覆盖有效面积为1.26 m2，降雨均匀度为82.3%，降雨强度为17.8 mm/h。累计降雨量见图7。

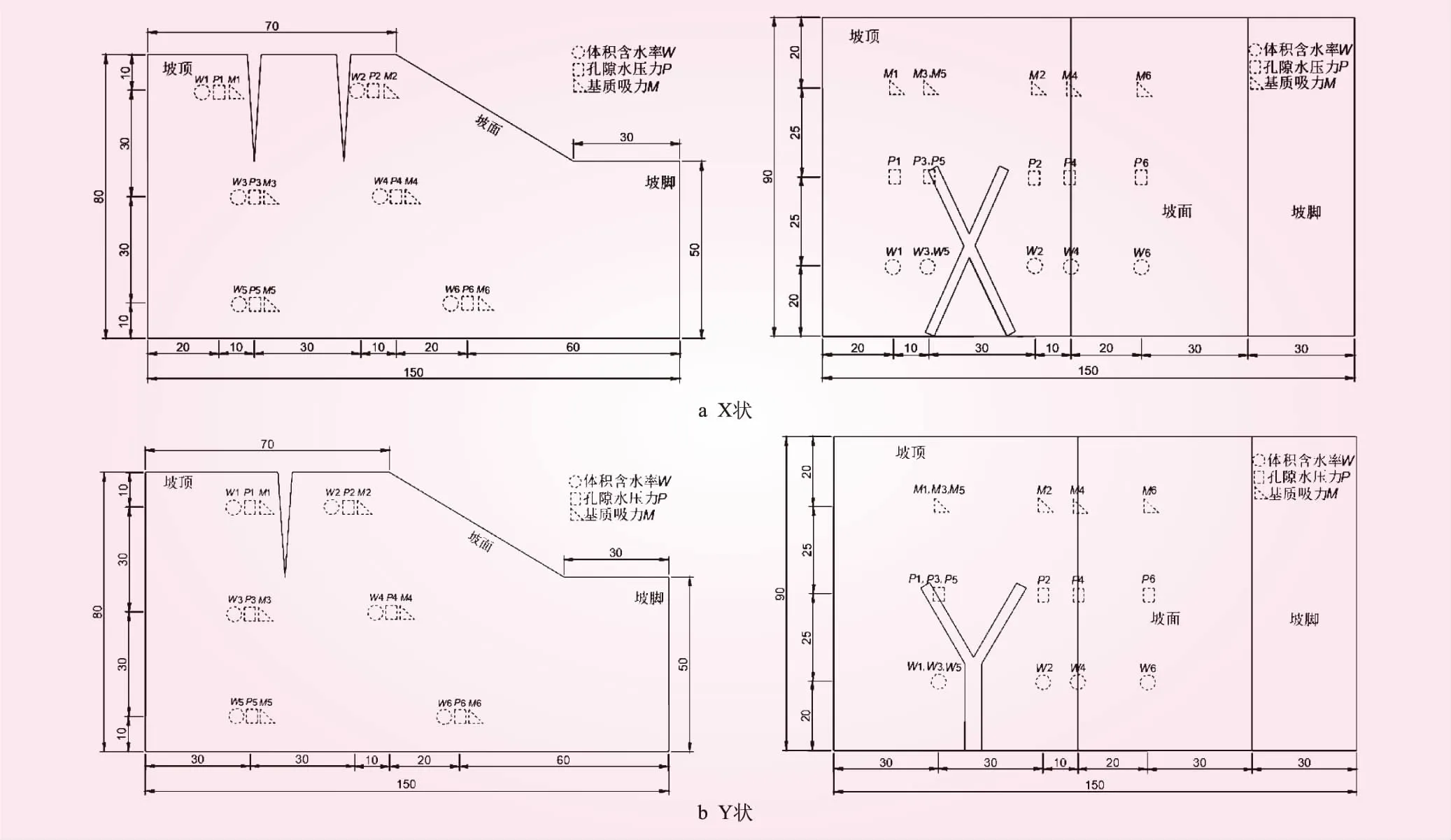
图6 模型正视及俯视模型(单位：mm)

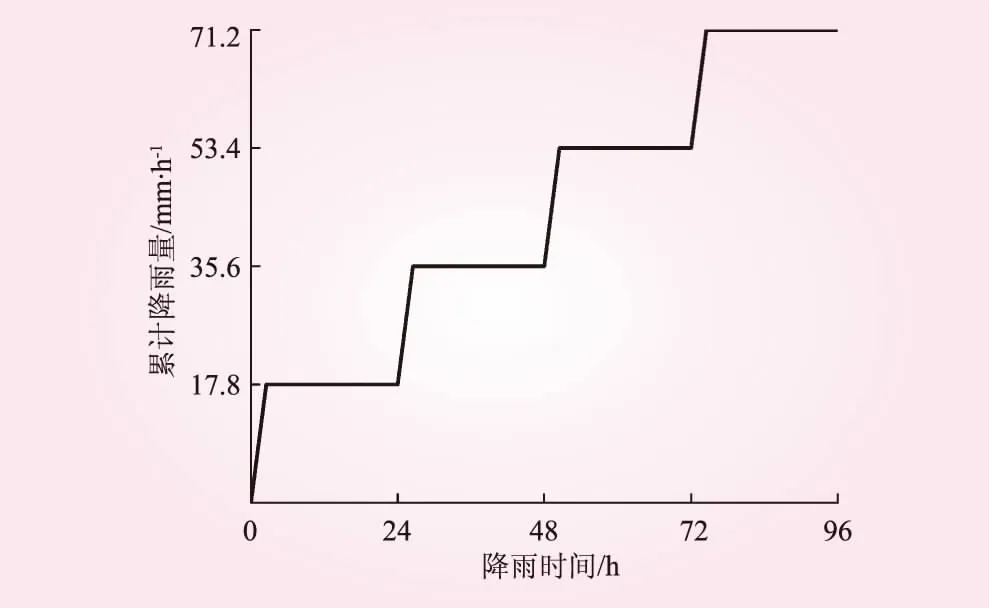
图7 累计降雨量

3 试验结果与分析

基于体积含水率、基质吸力、孔隙水压力等3项指标，对比X、Y状裂隙的变化，得到X、Y状裂隙渗透特性变化见图8。

3.1 体积含水率变化对比

从图8可知，X、Y状裂隙1、2号监测点均在第1轮降雨结束2 h内迅速响应，X状分别比Y状提前1.7、1.2 h。变化先期的X状近直立上升，上升速率较Y状快5.9%/h，随后都平缓上升至本轮含水率峰值，未见有回落趋势。2个测点X状初始含水率平均比Y状高0.8%，峰值也大3.2%。其后的3轮降雨，两者曲线形态均呈陡升陡降，同时以直立式增长达该轮峰值，而后快速回落，其过程较平缓。2个测点在响应时间上X状均比Y状提前1.1 h，但Y状峰值却始终分别大于X状峰值6.1%～11%、2%～3.7%，在回落过程中X状与Y状差距均在0.8%内。

X、Y状裂隙3、4号监测点则在第2轮降雨后3 h内响应，两者曲线形态随总时间均呈三级阶梯型。每轮降雨后2个测点X状均分别比Y状提前响应1.2、1.8 h，初始值差距在0.3%内，但各级平均峰值Y状分别比X状大2.9%、3.5%。5、6号监测点第三轮降雨后7 h时响应，X状2个测点分别比Y状滞后4.8、5.6 h，初始值差距均在0.5%内，但Y状峰值却始终大于X状(平均6%)，尤其在第4轮降雨后，两者峰值最大相差达到15%，但Y状回落的剧烈程度远远超过X状。

3.2 基质吸力变化对比

第1轮降雨后，X、Y状裂隙1、2号监测点在4.5 h内均响应，2号监测点X状比Y 状提前1.1 h，但由于仪器埋设原因，导致1号测点响应时间上比Y状提前2.8 h。两者开始响应时，吸力均出现陡降，下降速率Y状比X状慢1.76 kPa/h，随后都跌落至本轮吸力谷值。2个测点上X状的初始吸力平均比Y状大10 kPa，但谷值上Y状却分别比X状小2.1、8.3 kPa。在10 h时，X状出现明显回升，Y状则继续轻微跌落。其后的第3轮降雨，两者重复第1轮降雨变化趋势，但X状下降和回升幅度越来越小，两者最终都稳定在8 kPa左右。

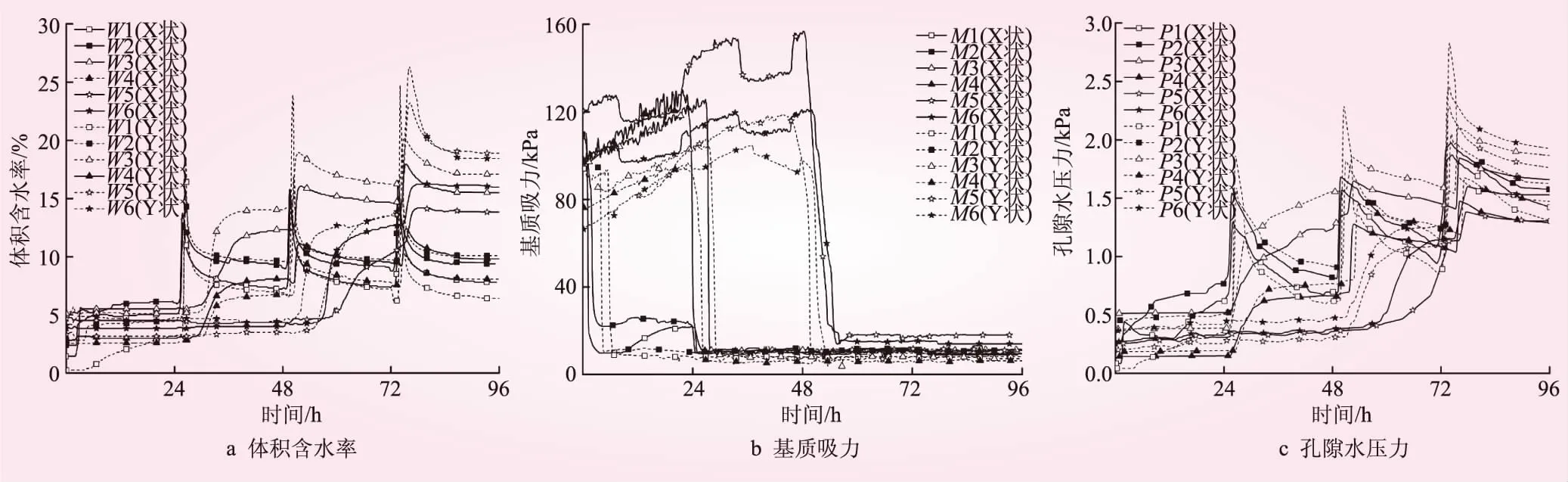
图8 X、Y状裂隙渗透特性变化

X、Y状裂隙3、4号测点均只在第1轮降雨期间出现波动跳跃急增段，而后直至第2轮降雨后2 h内响应，并出现断崖式骤降。X状2个测点的响应时间分别比Y状提前1、1.5 h，增后吸力也平均比Y状大20 kPa，但Y状谷值却平均比X状小4.2 kPa。后2轮降雨，两者响应后下降，但响应时间X状均比Y状快约1 h，Y状谷值却平均比X状小2 kPa，最终两者吸力值分别稳定在11.2、6.5 kPa。5、6号测点曲线变化趋势与3、4号相似，但X状的波动幅度较前更剧烈，2个测点均在降雨后6 h内响应，X状响应时间分别比Y状滞后2.9、3.8 h，增后吸力平均比Y状大30 kPa，但Y状谷值平均比X状小5.2 kPa，最终两者吸力值分别稳定在15.3、10.2 kPa。

3.3 孔隙水压力变化对比

第1轮降雨结束2 h内，X、Y状裂隙1、2号监测点均响应，X状分别比Y状提前2、1.3 h。变化先期的X状上升速率较Y状快0.5 kPa/h，但因X状2条裂隙侧的水分对向扩散，造成孔压在上升中受阻，数值稍有回落。其后的3轮降雨，两者响应同时，以直立式增长达该轮峰值，而后逐渐回落，回落过程中，X状与Y状吸力差距均在0.08 kPa内。2个测点X状均分别比Y状提前1.8、1.4 h响应，而在峰值上Y状却始终分别比X状高 0.2～0.3、0.4～0.7 kPa。

第2轮降雨后3 h内，X、Y状裂隙3、4号监测点响应，两者曲线形态随总时间均大致为三级阶梯型。每轮降雨后，2个测点X状均分别比Y状提前响应1.1、1.4 h，初始值差距在0.02 kPa内，但各级平均峰值Y状分别比X状高0.32、0.24 kPa。5、6号监测点第3轮降雨后8 h时响应，X状2个测点分别比Y状滞后4.8、6.2 h，初始值差距均在0.1 kPa内，但Y状平均峰值却始终比X状高1 kPa，尤其在第4轮降雨后，两者峰值最大相差达到1.6 kPa。

3.4 入渗阶段变化

X、Y状裂隙堆积体入渗变化阶段见图9。从图9可知，第1轮降雨刚结束时，X、Y状裂隙坡表土体被润湿，湿润锋显现且锋面与坡表大致平行，裂隙底部湿润区不明显。雨水入渗2 h时，裂隙底部湿润区均显现，湿润锋形态在此突变，裂隙处入渗深度平均比周围土体深20 cm。随着雨水持续下渗，水分差异性运移导致X、Y状裂隙湿润锋形态逐渐出现差别。在27 h时，X状底部2处独立湿润区由于前期的扩散，已汇合形成平缓下凹锋面，而Y状底部锋面下凹更深，面宽更窄。伴随湿润锋向下推移，X、Y状裂隙内外湿润区也均连通，平均入渗深度比周围土体大10 cm。到55 h时，X、Y状裂隙湿润锋随雨水入渗的进行进一步连通和扩大，总体均呈“W”形，而Y状底部锋面下凹程度比前期更深，且入渗深度实现对X状的反超。两者坡脚处湿润锋均已触底并向两侧发生水平渗透。历时至84 h，X状基本已被完全润湿，而Y状两侧还留有少许干燥区待完全润湿。

从上述入渗过程的外部现象可看出，裂隙相对于周围均质土体形成明显的优势路径，更快到达较深位置。X、Y状裂隙不同的展布形态对湿润锋的运移情况也造成显著影响，明显差异主要集中在裂隙底部的湿润锋形态上，X状底部因2处裂隙相近，随雨水入渗的进行，湿润区逐渐连通，汇合成宽缓弧面，从而加大侧渗范围。而雨水在Y状底部单独入渗，形成弧面更窄陡，下渗范围更大。

3.5 结果讨论

裂隙作为堆积体中的天然通道，加强了该处土体渗透性，促使雨水更快进入土体深部，相对于周围均质土体来说入渗更快。在降雨后期，土体逐渐饱和速率开始减缓，但也快于均质体。堆积体入渗全过程受到含水率、基质吸力、孔压的共同影响，最终会减弱其抗剪强度，可能造成该滑坡体的失稳破坏。根据轮次降雨顺序，对2种裂隙堆积体入渗的相应阶段进行观察，并结合渗透特性分析对比总结出其入渗机理，可概括为2个阶段：

(1)强烈入渗阶段。前期降雨大量汇集的雨水通过裂隙快速入渗，仪器响应迅速且渗透特性相应产生变化。X、Y状裂隙均在裂隙底部形成暂态饱和区，同时由于区内孔压激增，湿润锋不但向下迁移还逐渐与周围连通，最终形成椭圆形态。但2种裂隙发育不同的展布形态，导致X状优势路径作用更加突出，在堆积体的中上部具有更快的入渗速率，影响区域范围更大，相应椭圆区域也更宽缓，水平侧向渗透能力更强。而Y状汇水体积占优且独立集聚雨水，短时内水分竖向运移更多，造成渗透特性的变化程度更为强烈，相应椭圆区域更窄陡，垂直竖向渗透能力更强。

(2)稳定入渗阶段。后期降雨的水分不断累积，裂隙的存在使其底部的入渗速率明显快于坡体其他部分，体现出显著的优势入渗效果。X、Y状裂隙整体湿润锋依旧跟随前阶段趋势变化，湿润锋迁移速率却逐渐减缓，但受更高水力梯度影响，Y状底部的动水压力突增，直贯入渗突破下方土体，在堆积体的下部入渗速率较X状更快，造成两者椭圆区域形态差距也更为明显。

由于底板不透水，当坡脚位置湿润锋面到达箱底时，雨水竖向下渗受阻，只能向两侧扩散，2种裂隙底部水平侧向与垂直竖向渗透的差异依然如上阶段，但湿润锋仍持续下移，直到所有干燥区被润湿后，整个降雨入渗过程完成。