背风面合成射流作用下方柱绕流统计特性

2020-11-10王晋军

空气动力学学报 2020年5期

曲嫄, 王晋军

(北京航空航天大学流体力学教育部重点实验室, 北京 100191)

0 引言

合成射流是20世纪逐渐发展起来的新型主动流动控制技术。密闭空腔中振动部件周期性振动使流体经孔口周期性地排出和吸入，流体排出过程中在孔口处发生流动分离，进而卷起形成合成射流旋涡。

不同于传统的连续射流和脉冲射流，形成合成射流的流体来源于被控制的流场，合成射流向外部流场注入了动量而流经射流出口的流体净质量却为零。这一特性使合成射流系统具有无需额外气源、结构和加工简单、成本低、重量轻、维护方便、响应迅速等诸多优点[1-3]。合成射流在实际工程中被广泛应用于流动分离和气动力控制、射流矢量控制、增强掺混、加强传热传质、减弱噪声、防除冰、飞行控制和微流体控制等多个领域[4-6]。

Glezer采用量纲分析与实验观察相结合的方法，提出表征合成射流涡环特性的Slug模型，即采用无量纲冲程和合成射流雷诺数两个无量纲参数来描述合成射流涡环的结构特征[7]。随后，Smith和Glezer在对狭缝合成射流的研究中指出，该模型也适用于刻画合成射流涡对[8]。无量纲冲程决定了吸程开始时合成射流涡环/涡对与合成射流出口之间的距离，亦即两个相邻周期产生的合成射流涡结构的间距[9-11]。Shuster和Smith在研究圆形出口合成射流的实验中发现，当无量纲冲程过小时，吹程形成的合成射流涡环吸程会被重新吸入合成射流腔体[10]。Zhong等的研究表明，无量纲冲程还与合成射流主涡环承载的最大环量有关。当无量纲冲程超过4，主涡环的环量不再随无量纲冲程的增大而增大，主涡环之后会生成二次涡[9]。合成射流雷诺数则决定了合成射流涡的强度，与无量纲冲程共同影响涡结构的状态[10-12]。Shan和Wang在对静水环境下涡环的研究中发现，随着合成射流雷诺数增加，涡环从层流变为湍流，其结构更易失稳和破裂[12]。基于染色液流动显示的结果,Shuster和Smith得到不同无量纲冲程和合成射流雷诺数下涡环转捩的图谱[10]。

在应用合成射流对钝体和翼型绕流进行流动控制的研究中，除合成射流的属性外，往往还关注合成射流与自由来流的相对关系，此时，常引入另外两个无量纲参数：合成射流动量系数和无量纲激励频率。前者表征合成射流与自由来流的相对强弱，后者则表示合成射流的激励频率相对于流场特征频率的大小。Feng等在圆柱的后驻点施加狭缝合成射流控制圆柱的绕流流动，并讨论了各无量纲参数对控制效果的影响。结果表明，无量纲冲程和动量系数是影响尾迹涡脱落模式的重要参数[13]。

本研究采用活塞式合成射流激励系统来形成合成射流。若合成射流的出口尺寸一定，无量纲激励频率、合成射流雷诺数以及无量纲冲程中有两个参数相耦合。在此前应用背风面合成射流控制方柱绕流的研究中[14]，无量纲冲程不变，改变无量纲激励频率，合成射流出口速度和合成射流雷诺数随之变化，从而影响合成射流的控制效果。本研究则在维持相同的合成射流雷诺数，即相同的合成射流平均出口速度的条件下，同时改变无量纲激励频率和无量纲冲程，比较了不同参数组合下方柱绕流流场的统计学特性，揭示了这两个无量纲参数对时均流场和合成射流减阻效果的作用规律。

1 实验装置及参数

实验在北京航空航天大学低速循环水槽中进行。该水槽实验段长3000 mm，截面尺寸为600 mm×600 mm，自由来流流速可在0～500 mm/s的范围内连续变化。本实验中自由来流速度U∞=43.8 mm/s，该流速下自由来流湍流度小于0.8%。

方柱模型如图1所示。方柱边长D=20 mm，展长430 mm。沿方柱背风面的中心线设有一道狭缝，作为合成射流出口。狭缝长度l= 100 mm，宽度w=1 mm。方柱内部沿轴线有一直径14 mm的柱状空腔，其一端封闭，另一端接进气口，通过有机玻璃管和聚四氟乙烯管连接至合成射流激励系统。图2是实验装置示意图。为了保证测量区域附近流场的二维性、减小水槽壁面边界层发展对流动的影响，在方柱两端顺流向加装端板，端板的前缘做了切尖处理。方柱水平固定于端板的中间高度。以方柱的几何中心为坐标原点建立直角坐标系，各坐标轴方向如图1、图2所示。

图1 实验模型示意图Fig.1 Sketch of the experimental model

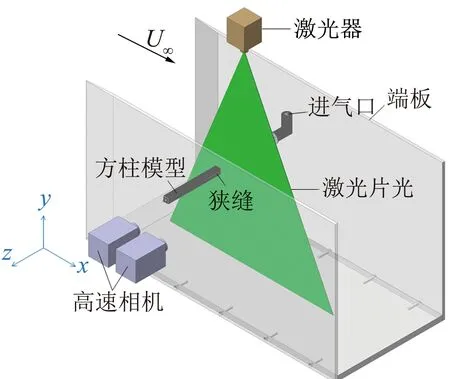
图2 实验装置示意图Fig.2 Schematic of the experimental set-up

本实验采用了与文献[14-15]相同的活塞式合成射流激励系统。伺服电机带动同轴的偏心轮旋转，进一步由曲柄滑块机构带动激励器的活塞在缸体内往复运动。本实验条件下，不考虑激励器、连接管路以及方柱腔体内流体的压缩性。在正弦型信号的激励下，方柱腔体内的流体经背风面的狭缝周期地排出和吸入，产生合成射流涡对。合成射流的瞬时出口速度可表示为:

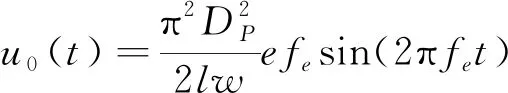
(1)

(2)

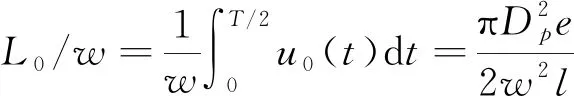
(3)

(4)

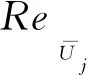
表1 各工况的参数设置Table 1 Parameters for different cases

采用时间解析的二维粒子图像测速技术(TR-2DPIV)测量方柱绕流流场，实验平台如图2所示。激光片光由波长532 nm的连续激光器提供，沿x-y平面照射于方柱半展长位置。示踪粒子为直径5～20 μm、密度1.05 g/cm3的空心玻璃微珠。沿流向布置两台高速相机来记录粒子图像。上游和下游相机的空间分辨率分别为1792 pixel×1440 pixel和1280 pixel×2048 pixel，拍摄视野的尺寸约为161.5 mm×129.4 mm和167.5 mm×270.4 mm，对应的图像放大率约为0.09 mm/pixel和0.13 mm/pixel。各工况相机的采样频率在表1中列出。采用多通道迭代的Lucas-Kanade算法计算PIV速度场[16-17]。查询窗口大小为32 pixel×32 pixel，窗口重叠率为75%。至少26 100帧瞬时速度场被用于计算各工况的速度统计量。

2 实验结果分析

2.1 合成射流对方柱近尾迹时均流场的影响

不同合成射流参数组合下，方柱绕流的时均流动结构如图3所示。无控制工况下，方柱前缘棱角处发生流动分离而形成回流区，回流区延伸至下游鞍点处。当(fe/f0,L0/w)=(1.0, 145.3)时，合成射流的吹吸作用使得方柱背风面附近形成一个小回流区，但该回流结构关于y=0不对称分布。推测不对称分布的原因为，合成射流从出口排出后受到方柱尾迹涡的诱导，向y=0的上侧或下侧偏转，不同偏转状态在时间上分布不均衡。Huang等[18]在采用背风面连续射流控制方柱绕流的研究中，在注射比(连续射流的平均出口速度与自由来流的速度之比)IR=1.0时，也观察到连续射流受尾迹涡诱导而发生偏转的现象。不同的是，连续射流的偏转方向随着尾迹涡的脱落而发生周期性变化，而(fe/f0,L0/w)=(1.0, 145.3)工况下合成射流的偏转无周期性。受合成射流的影响，该工况下因前棱角处流动分离而形成的主回流区也关于y=0不对称，且鞍点位置向下游推移，回流区变长。对于工况(fe/f0,L0/w)=(2.0, 72.7)，通过观察瞬时流动发现，合成射流涡对与剪切层、尾迹涡之间的作用显著。合成射流向尾迹流场注入动量，时均流线图中方柱下游y=0上负的流向速度几乎消失，合成射流主控了尾迹区流场。因合成射流作用，方柱绕流的回流区尺度大大减小，分布于方柱后棱角附近。在y=0两侧流向位置x/D=1.2附近形成两鞍点。当(fe/f0,L0/w)=(4.0, 36.3)时，合成射流形成的回流区被包裹于主回流区内，主回流区相比于(fe/f0,L0/w)=(1.0, 145.3)工况进一步向下游延伸，长度显著增大。除主回流区末端的鞍点外，两回流区之间有新鞍点形成。(fe/f0,L0/w)=(5.0, 29.1)工况下，合成射流涡对较弱，射流出口附近可见合成射流引起的流线变化，但回流不明显。主回流区结构和无控制工况类似，长度略微增加。

图3 各工况方柱绕流的时均流线图Fig.3 Time-averaged streamlines around the square cylinder for different cases

图4 各工况的时均雷诺应力分布图 Fig.4 Distributions of time-averaged Reynolds stresses for different cases

2.2 合成射流对方柱绕流的减阻效果

Antonia和Rajagopalan在其文章中指出，圆柱的阻力系数可由某一流向位置的时均速度剖面积分求得[19], 阻力系数由动量积分项CD1和雷诺应力的贡献项CD2两部分组成，如式(5)所示：

(5)

式中，U代表时均流向速度。上述公式也可用于方柱绕流阻力的计算[14, 20-22]。本文对流向位置x/D=10处的速度型沿垂向积分求得阻力系数。受实验拍摄范围限制，实际垂向积分范围为-6.5≤y/D≤6.5。图5为x/D=10处速度统计量的垂向分布。各工况的时均流向速度U仍存在明显亏损。在方柱背风面施加狭缝合成射流可加快流向速度亏损恢复，亏损由大到小依次为无控制工况，工况(fe/f0,L0/w)=(5.0, 29.1)，(2.0,72.7)，(1.0, 145.3)和(4.0, 36.3)。各工况流向速度脉动强度urms均为典型的双峰分布。无控制工况的流向速度脉动最强，有控制工况的流向速度脉动强度均不同程度降低。工况(fe/f0,L0/w)=(5.0, 29.1)，(2.0, 72.7)，(1.0, 145.3)的urms值相近，(fe/f0,L0/w)=(4.0, 36.3)工况的流向速度脉动水平最低。垂向速度脉动沿垂向为单峰分布，合成射流也显著降低了该流向位置的垂向速度脉动水平，vrms的值由大到小依次为无控制工况，工况(fe/f0,L0/w)=(5.0, 29.1)， (2.0, 72.7)，(1.0, 145.3)和(4.0, 36.3)。对比发现，时均流向速度亏损和速度脉动强度随合成射流参数的变化规律基本一致。

基于上述速度分布，应用公式(5)求得各工况的阻力系数和减阻效果如表2和图6所示。可见，各控制参数下合成射流均起到一定减阻效果，小激励频率大冲程和大激励频率小冲程的工况对应的减阻效果一般。减阻效果最好的是无量纲激励频率和无量纲冲程均中等的工况(fe/f0,L0/w)=(4.0, 36.3)，减阻率达53.7%，其次为工况(fe/f0,L0/w)=(1.0, 145.3)和工况(fe/f0,L0/w)=(2.0, 72.7)。工况(fe/f0,L0/w)=(5.0, 29.1)减阻作用较弱，阻力系数和无控制工况接近。对照图3、图4和图5中的结果，减阻率最大的(fe/f0,L0/w)=(4.0, 36.3)工况的回流区沿流向延伸最长，雷诺应力水平最低，时均流向速度亏损恢复得最快，流向和垂向速度脉动强度最低。这些统计量的改变与该工况下靠近方柱的尾迹区域内尾迹涡趋向于对称脱落有关。

图5 x/D=10处的速度剖面图Fig.5 Profiles of velocity statistics at x/D=10

表2 各工况的阻力系数及减阻率Table 2 Drag coefficients and drag reduction rates for different cases

图6 方柱阻力系数随合成射流激励参数的变化Fig.6 Variation of the drag coefficient of the square cylinder with the excitation parameters of the synthetic jet

将y=0上时均流向速度变为0的位置到钝体轴线的流向距离定义为回流区长度[23-24]。图7给出了y=0处时均流向速度的沿程变化。在此，结合图3来比较图7中各曲线的变化趋势：无控制工况下，U/U∞随x增大先减小后增大，最后趋于稳定，其中，U/U∞为负值的区域对应图3(a)中的尾迹回流区；对于有合成射流控制的工况，随着x增大，U/U∞先增大后减小再增大，U/U∞在方柱背风面附近的第一次增大是受到合成射流向流场中注入动量的影响。工况(fe/f0,L0/w)=(2.0, 72.7)，方柱绕流的回流区位于后棱角附近(图3(c))，尾迹中心线无回流，U/U∞沿x轴无负值。对于工况(fe/f0,L0/w)=(5.0, 29.1)，(1.0, 145.3)和(4.0, 36.3)，随x增大，U/U∞由正变负的位置表征合成射流诱导产生的回流区长度，U/U∞由负变正的位置则表征方柱绕流主回流区长度。对比图6的阻力系数，主回流区长度越长，合成射流的减阻效果越明显。