《营造法式》上、下昂斜率取值方法探析

喻梦哲

惠盛健

一、引言

关于《营造法式》（以下简称《法式》）的用昂制度，既往研究成果非常丰富，但对于其角度的取定原则却尚无定论，亟需加以解决。

广义的“昂制”研究始于梁思成[1]借助现代制图方法重释《法式》文本的努力；此后陈明达[2]、潘谷西[3]等人的研究则利用斜昂份数旁证材份制度在屋宇设计中的作用；刘畅通过大量田野调查所获取的精确数据，梳理出宋代木构建筑下昂角度采用整数比的普遍规律；陈彤[4]则创造性地利用关联构件的尺寸信息反证出下昂的轮廓比例关系，为启发后续讨论提供了可能。

一个显见的问题是，《法式》精确记载了转角诸昂的长度，若其所指是水平投影长，则与制度部分记载的出跳份数不符；若所指是实长，则必须存在确定的倾斜角，才能令其投影距离与制度规定相一致。那么这个角度如何求取呢？

本文主要以斜昂首尾位置的厘定为出发点，通过作图分析了①交互枓归平的约束条件、②昂尾挑斡平槫的欠高矛盾、③昂方交接的榫卯逻辑等关键问题，推导出《法式》不同等级铺作用昂斜率的理论算值，以期揭示出隐匿于文本中的斜昂倾角设计规律。

二、下昂斜率设计的基本分类与约束条件

考虑到中国古代工程营造中“几何问题代数化”的数学传统[5]，昂的角度或应采用契合于勾股比例的“率”而非切分圆弧的“度”来表达。[6]影响下昂斜角设计的因素主要有三项：其一是昂势的峻缓权衡，体现为昂端与扶壁上的交互枓是否齐平；其二是昂身的榫卯处理，体现为昂过扶壁栱、方时两者上下缘是否对位；其三是昂尾的收止方式，体现为压跳或挑斡等操作措施与屋架设计间是否联动。正是对于这三项指标回应方案的差别，勾勒出了不同匠系间的技术边界。

元代以前的遗构，若按照“昂制”逐条析分，对号入座，则大抵存在三类不同的做法（图1），我们姑且称之为“唐辽型”“榆林窟型”（因最早见于榆林16 窟壁画楼阁）和“法式型”[7][8]，归结其主要差异为表1。

图1：三种铺作类型中昂上交互枓的归平倾向差异示意

总括而论，“唐辽型”流行时段最早，且多用于殿阁类建筑，本身也符合井干堆叠的原始逻辑，其下昂斜率遵循“每平出一大跳（当偷心造两跳之和）抬升一足材”的基本原则，昂仍从属于铺作自身的材栔格线，跳头上交互枓隔跳与施于正心缝上者归平。在此线性思维导引下，昂与扶壁栱、方边缘对齐，榫卯制备简单均一，后尾亦完全组织于联系屋架的内外柱列叠方之中。“榆林窟型”下昂的形象最早见于五代绘制的榆林十六窟壁画楼阁，符合其构成原则的宋金实例亦为数不少，它的进步在于以“每平出一跳抬升一单材”的原则因应计心造普及的事实，赋予外跳上交互枓按实际需要定高的优先权，以此克服“唐辽型”过于机械以致无法灵活调整檐口的缺陷——但其调节能力有限，最终仍需保持昂身与扶壁栱、方交接关系的相对简明（上下缘及中段可随意组合对齐，但不允许产生无序的错缝），至于后尾则通过在昂下放置诸如昂桯、挑斡之类的垫块，使之与屋架设计略微脱钩。总的来说，它对昂的首尾两端控制较为严格，而中段可稍作损益，适用性最好，分布也最广泛。“法式型”则最为杂糅，缺乏如前两者般鲜明的下昂抬升原则，对于上述三个问题的解决都不甚彻底，也因而留下了大量调整余地，这是间取百家之长的必然结果。

“唐辽型”“榆林窟型”及“法式型”铺作昂制异同一览 表1

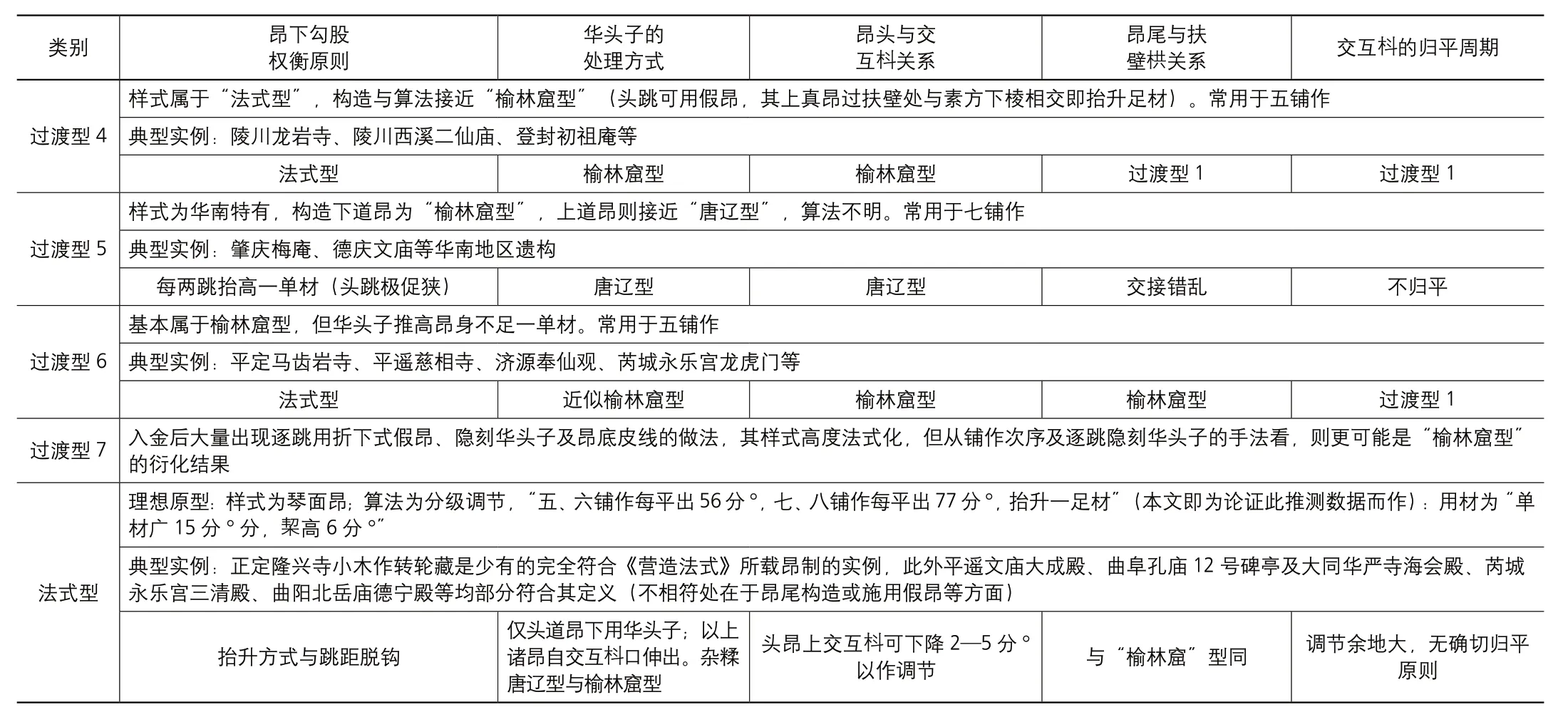
续表

三、外檐“形式优先”的意匠选择与《营造法式》的下昂斜率设计

按《法式》卷四“飞昂”条的记载，官式斗栱需坚持逐铺出跳（不能采用闽粤沿海一带常见的叠昂而不出跳做法），其头道昂上、下的交互枓与华头子均有严格的高度分位设定。同卷又引述了铺作里转的三种“经久可行之法”，总的原则是藉由承槫的需求令铺作与屋架在设计上产生联动，这样昂的斜角自然应当服从于举折之制，而问题也随之产生——与我们在佛光寺东大殿[9][10]上所见的不同，《法式》记录的下昂斜角明显缓于檐椽，以至于在殿阁和厅堂中分别需要借助上叉蜀柱，或用挑斡、昂桯挑一枓至一材两栔的方式去填平昂尾与平槫间的欠高。李诫为何不直接增大昂的斜角来消弥其后尾与槫位间的空隙，而是执意在槫下加塞杂件？这导致下昂两端的荷载传递都变得更为曲折，徒增失稳的风险。

若从外檐形象上寻求解释，则不难归因于宋以后补间铺作发达的事实：一方面，密集的昂尾共同斜升挑槫加强了构架的整体稳定性，但另一方面，因需与柱头铺作保持形态一致，导致下昂折角与屋面的举折设计不相统属，产生的差值需借助蜀柱、昂桯等构件“随宜枝樘固济”。或许在北宋官式建筑的营造中，维持外立面“檐牙高啄”“整饬如一”的需求是居于首位的，其他不如意处只能暂时隐忍。这种内、外檐形象的割裂，根源在于唐辽以来铺作设计中“构造优先”传统的没落[11]，而跳距的增减、昂上交互枓的升降等调节措施，则都是为了形成固定的下昂斜率，从而保持立面形象均齐的变通手段。

四、《营造法式》五、六铺作下昂的斜率生成规律

昂身的斜率可以藉由耍头实长、耍头与昂间高差这组勾股数逆推得到。陈彤引述《法式》卷十八“殿阁外檐转角铺作用栱枓等数”中记载的耍头数据，在假设其下交互枓外棱刚好与昂嘴后缘接缝时，算得该处空隙在71 分°（耍头长65 分°+交互枓底半长6 分°）的平出距离内抬高了27 分°（一材两栔），故下昂斜率应为27/71[12]。这一推论所得数据畸零，与实例测值经常出现的四、五举整数比并不符合。

实际上，《法式》在处理横栱与出跳栱、昂节点时，总会预留出过渡部分，以令接触面尽量自然。设使交互枓自昂上皮外缘稍稍内移，一则可令昂面内䫜曲线起势和缓，减轻交互枓坐于斜面边缘的不稳定感，二则降低了因鹊台糟朽连带牵扯交互枓歪闪的风险。卷二十九“绞割铺作栱昂枓等所用卯口第五”所录下昂分件图样中即明确表达了这一突出于枓底外缘的平台（图2），若定其长为1 分°，则《法式》五、六铺作的下昂斜率可化简为 27/（65+6+1）=3/8，这一取值显然更便于工匠记忆和操作。

我们从三个方面验证该推测值的合理性。

其一是跳头交互枓下降份数简明与否。《法式》规定六铺作以下“理论上”不减跳，逐跳出30 分°即两材广，此时昂、栱上交互枓保持齐平，跳头横栱与扶壁栱亦投影重合。但从功限部分可知跳距折减现象是实际存在的，如“六铺作用瓜子栱

图2：明清官式斗栱中残存“鹊台”意向与《营造法式》中耍头、合角下昂及斗件等榫卯图样

列小栱头分首两只，身长二十八分；瓜子栱列小栱头分首两只，身内交隐鸳鸯栱，长五十三分”，由于28 分°×3/8=10.5 分°

即半足材广，因此该处减跳值或是基于唐辽殿阁偷心造铺作中“每两跳合计升降一足材”的约束原则取得的，李诫在斟酌跳头交互枓下降份数时大概部分借用了唐官式的传统。

其二是与斗栱分件图样透露的榫卯细节吻合与否。按卷三十“绞割铺作栱昂枓等所用卯口第五”中绘制的里跳耍头（角内用，七铺作以上随跳加长）形象，其前端开口并塞入齐心枓下，且未越过心缝。设若《法式》下昂斜率大于3/8，则其过泥道处位置应高于齐心枓口外棱，此时华头子与下昂在柱缝外的部分将产生三角空隙，要么对其放任不理，要么需令里跳耍头越过柱缝后予以补实，而这两种处置方案都与图样信息不符，反过来也证明了推定的下昂斜率上限取值是难以跨越的 （图3）。再看枓的加工情况，同卷中绘制了泥道栱上与令栱上用齐心枓各一种（前者枓底抹斜放过昂身），设若下昂过扶壁时底皮低于齐心枓口外棱，则必抹斜枓口以利于承托昂身；反过来若高于枓口外棱，则为了凑足欠高，枓平将高于2 分°或在枓内垫塞木块。事实上两种情况亦未曾发 生[13]，这说明《法式》的榫卯设计极度精细，只允许下昂底皮恰与齐心枓平外棱重合这一种情况存在，此时昂的斜率定格在27/72即3/8，别无变动的可能，它略微比四举即28/70平缓一些。

其三是昂与柱缝上素方的搭接关系理性与否。以推定的3/8斜率作图验算，发现下昂底皮恰好切于泥道栱上齐心枓口外沿，这正是我们期待中的理想情况：昂尾向后延伸时，或是与心缝上栱、方边棱相合，或是从扶壁上齐心枓口外棱吐出，构件间的控制线与结构线相互恰合，为设计和施工带来了极大的便利。

质言之，《营造法式》选录一种恰当而固定的下昂斜率是可信的，其数值选择与生成机制均有别于唐辽时期的技术传统，表现为跳头的空间定位彻底突破了柱缝上的材栔格线。我们知道早期殿阁的一个重要构造特征是跳头上交互枓与扶壁上齐心枓取平，即或补间用卷头造，柱头用下昂造，相同层数的昂与华栱端头也是对齐的，以此保证罗汉方拉通整圈外檐铺作。这也证明了昂上交互枓的分位（也就是外挑部件的空间定位）因变于扶壁上栱、方的材栔堆叠关系，昂的倾斜程度完全受制于华栱层层推高、伸出后形成的空间矩阵，是非常不自由的。五代以降，柱头与补间铺作形态趋同，通过同步调整同层栱、昂上的交互枓位置，即可保证罗汉方拉通，跳头的空间分位设定逐步与扶壁上的材栔格线脱钩。同时，下道昂不再自交互枓口内直接伸出，而是垫在露明的华头子上，其起算点抬高了近10 分°，这就从根本上瓦解了过往的下昂组织逻辑。李诫规定四、五铺作交互枓直接归平，六铺作以上藉由微调跳距归平，入宋以后度量与加工技术的进步、模数制度的进化，都使得繁难而精确的操作成为可能，设计原则也由简明单一走向复杂灵活。

图3：《营造法式》五、六铺作下昂斜率推算方式示意

五、《营造法式》七、八铺作下昂的斜率生成规律

前人研究中的一个主要困扰在于，《营造法式》大木作制度部分给出的出跳份数与功限记载的构件长度间常有抵牾，如卷十八“殿阁外檐转角铺作用栱、枓等数”记载“八铺作至六铺作各通用：瓜子栱列小栱头，两只，身内交鸳鸯交首栱，长五十三分……慢栱列切几头分首，两只，外跳用，身长二十八分……。”这种以25分°和28分°组合构成减跳后跳距的做法，与制度卷内规定的标准跳距30 分°和减跳跳距26 分°并不相同，到底孰是孰非？

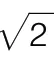
如前所述，李诫在设定下昂斜率的过程中应是充分考虑了外檐形象问题。参考大雁塔门楣线刻佛殿等图像资料，可知盛唐以来的传统是令跳头与扶壁的横栱间投影重合无交错，以此确保横栱看面完整展现；如遇下昂造，则要么隔跳归平，要么间用偷心，以达成同一目的。因扶壁栱上遮椽版平置，故栱方、昂方间的交叠关系悉数裸露，所有构件均倾向于垂直对缝，补间铺作或大幅简化（减跳），或干脆缺失，栱间壁版更多地以彩绘图案装饰，而非密布斗栱以呈现结构之美。随着逐跳重栱计心做法日益盛行，若保持下昂首尾端点不变，则每跳均下降半足材，各跳头上横栱间势必交错遮挡[自令栱以内，逐层遮掩（15-10.5）/15 即约1/3的栱件身广]，绵密堆积使得外檐形象从疏朗井然走向繁复杂乱，这就引发了调整昂身斜率以使诸横栱重新归平的需求。

此时有两种方案可供选择。其一是延续唐辽以来的构造逻辑，令昂尾坐于泥道栱上齐心枓内，并与扶壁上素方正交，绕此点旋转昂身并加长头昂下的华栱挑出长度，从而放缓下昂，直至各跳上横栱重新归平。但这将带来额外的构造问题：明栿端头绞入铺作后充华头子，其前端被砍削为过度尖细的三角形木楔会导致梁身承载力下降过剧，同时华栱与下昂跳距分配失衡，因此并不足取。其二则是彻底推翻唐辽以来扶壁栱方必与昂身边缘对齐的传统，优先满足外檐形象的整饬均平——这也正是李诫的选择，结果导致了新的下昂斜率取值。作图可知，当每隔25 分°跳长降低7 分°垂高时[14]，各跳头横栱间仅上下错缝1 分°，这恰好是开刻的栱眼深度（图4）。

我们从四个方面论证推想斜率值的合理性。

肛瘘属于临床上一种较为多见的肛肠科病症，系指肛门邻近的肉芽肿性管道，由内口、瘘管、外口构成［9］。按照全国肠肛协会会议制定的肛瘘分类标准，可将肛瘘分成单纯性肛瘘、复杂性肛瘘、马蹄形肛瘘三种［10］。其中，复杂性肛瘘的结构较复杂，瘘口数与管道分支均较多，涉及区域较广，位置较深，临床诊断与治疗均存在一定的难度［11］。诊断过程中应重点确定肛瘘的内口位置、瘘道数、走形情况及其与邻近肌肉的关系等，若肛瘘的内口位置与瘘道数无法判断，则治疗时可能出现内口处理的遗漏，进而导致疾病复发［12］。

首先，通过作图考察铺作构件搭接的自洽性。据《法式》卷十八“殿阁外檐转角铺作用栱、枓等数”条记，“交角昂：八铺作六只，两只身长一百六十五分，两只身长一百四十分，两只身长一百一十五分。”代入3/11斜率后发现各项数据均能吻合[15]，此时六、七、八铺作中仅头昂上的交互枓可在2—5 分°范围内调整，用于二昂以上者均不在可调之列，可知所谓“凡昂上坐枓，四铺作、五铺作并归平，六铺作以上自五铺作外，昂上枓并再向下二至五分……”其实是不包括七、八铺作的，这是因为自第二道以上诸昂均直接从交互枓口内伸出，并不经由华头子的垫托，升、降斗口位置能起到的调节作用十分有限，在跳距与昂身垂高不变的前提下，唯有赋予下昂合适的斜率才能解决问题。

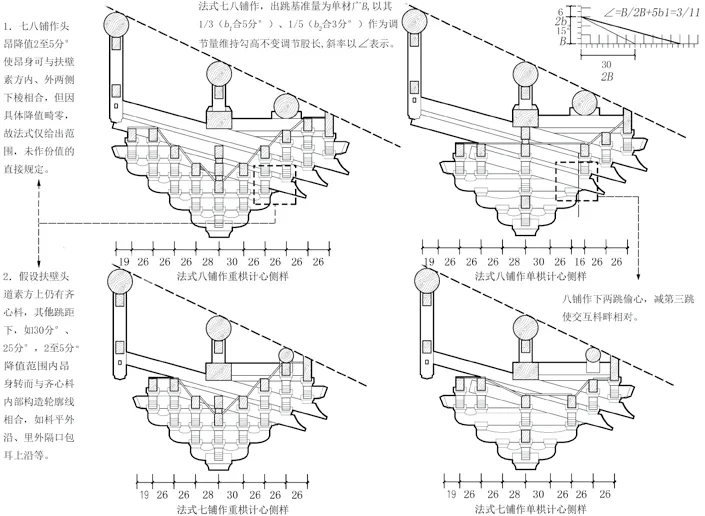
图4：《营造法式》七、八铺作下昂斜率推算方式示意

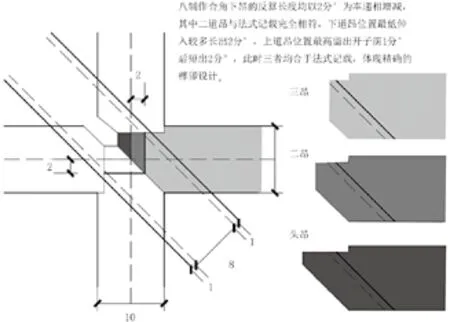
图5：角缝昂实长验算及榫卯做法分析

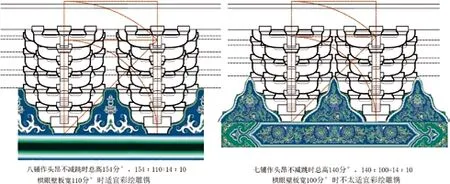
图6：铺作立面比例关系示意

图7：《营造法式》四铺作插昂斜率推算方式示意

取推想斜率时角昂反算值与正身昂实长份数验证情况 表2

其二，椽长、朵当、举折等空间数据的阈值为昂的斜率算定提供了旁证，两者间不应出现矛盾。卷五“椽”条记载了厅堂与殿阁的椽平长上限分别是6 尺与7.5尺，以卷十七“殿阁外檐补间用栱枓等数”条所记各昂长度代入3/11斜率后作图发现，其八铺作昂身里转投影长125 分°，选一等材时恰合7.5 尺，与制度部分的记载完全吻合（图4）。此外，诉诸地盘图样亦可得出类似结论，如卷三十一“殿阁地盘分槽等第十”图中所绘规模最大的“殿阁身地盘九间，身内分心斗底槽”平面，按最大进深十二架椽、椽长7.5 尺，深四间、逐间双补间计算，得出侧面朵当长也是125分°，与前述结论一致；若七铺作，则算得昂身投影长120 分°，用一至三等材时分别折合7.2 尺、6.6 尺与6 尺；若六铺作，无论双杪单昂或单杪双昂，昂身投影恒长100 分°（它规定了朵当下限，使得相邻慢栱不至于相犯）。综上，《法式》首步架平长、朵当及昂身实长的计算是一个圆融互恰的整体，下昂斜率的设定必然受其制约。

其三，《法式》记载了角缝逐道昂的实长份数，以推定的斜率反算其不加斜时对应于补间的实长，若其与后者的记载值吻合或接近，则可辅证推论的准确性 （图5）。从表2 算得数据的自洽程度看，推想值的可信度是较高的（考虑到转角处诸昂后尾均需共同挑托平槫交圈节点，适当放大长度以备加工时临时截割实属合理）。各组算值中，最上道昂都略有讹大而整体误差最小，这就保证了整组下昂的基本挑斡能力；反之所有下道昂的离散趋势各不相同，六、八铺作偏短而七铺作偏长（表2）。

六、《营造法式》分级表述下昂斜率的内因分析及其取值方式溯源

综上，《营造法式》文本中可能暗示着三个固定的下昂斜率取值，即四铺作插昂取3/5，五、六铺作取3/8，七、八铺作取3/11，是什么导致了这种差别？

一般认为六铺作表征着李诫默认的建筑等级拐点，它本身具有较大的特殊性，在文本中也被一再提及。我们试以六铺作举例，通过考察昂尾挑斡的构造问题来回答为何需要将昂身斜率分为峻缓不同的两级（不算插昂的特殊情况）。

总的看来，《法式》体系追求的是建筑外立面的整洁有序，尤其是外檐斗栱的圈层均一，这要通过增加朵数、同化外观、平分朵当以及拉齐各跳上横栱来达到，而最终的实现途径是放缓昂 身[18]——为此付出了两方面的代价，其一是放弃扶壁栱方与下昂间的对齐关系，两者上下缘间无序的错缝交接导致榫卯开口繁难；其二是昂尾与槫底间欠高加剧，无法直接以下昂挑斡解决而必须引入更多垫块，导致传力路线不单一。

第一个问题尚属于可控的范围——由于提倡双补间，扶壁部分的装饰意味已被大幅削弱，栱眼壁版被分散打断，不再是彩画描绘的重点；同时因遮椽版斜置，扶壁栱逐渐由“I”字形竖向叠垒转变为“V”字形分散排布，大部分井干壁皆不可窥见，因此无论下昂与柱缝栱方间交接错乱与否均无碍观瞻。当然，李诫仍在尝试延续唐辽以来横栱素方与昂身边缘对齐的传统，关于六、七、八铺作昂下交互枓较里跳下降2—5 分°的规定正源于此。按3/11斜率作图发现，下降2 分°时七、八铺作昂身下皮恰与扶壁素方外侧下棱相合；下降5 分°时略与扶壁素方里侧下棱相合[19]，当采用这两个极限值之一时可部分保留唐辽以来昂、方边缘对齐的传统，对于彻底解决错缝问题则并无帮助——实际上遮椽版掩蔽后的“不可见”也导致柱缝上的昂方错缝不再成为一个问题。

第二个问题则更为严重——当七、八铺作采用3/11的下昂斜率时，昂与檐椽间产生了较大的斜角差值。按《法式》举折之制，殿阁与厅堂的首架斜率分别达到0.49 和0.45[20]，这个习用值放在椽、昂近乎平行的唐辽殿阁上并无不妥，在《法式》中则因昂身放缓而产生了无法弥合的槫下欠高，叉昂尾的蜀柱和垫槫底的一材两栔也应运而生。七、八铺作殿阁因昂尾远在草架之上，问题尚不明显，六铺作厅堂的情况则微妙得多。作图可知，最高等级的“八架椽屋乳栿对六椽栿用三柱”厅堂侧样尚可勉强以昂尾直接挑斡平槫（前提是越级采用殿阁径两材的下平槫，且替木高12.25分°而非12 分°）；若严格采用厅堂 “加材一栔或三分”的槫径取值，或是只用四、五铺作，则仅靠铺作自身根本无法凑齐与槫底间的空缺，从而需要为低铺数的斗栱设置更为陡峻的下昂斜率。由此观之，六铺作正是处于昂尾挑斡平槫能力的临界点上，此时槫径取值已达极限，若首步屋架趋陡或是架深增大，都会导致平衡被打破，此时只能引进昂桯挑斡做法予以解决。

正是因了这种戏剧性的“定格”，六铺作必然成为昂身斜率设定的分水岭，低、高铺数斗栱各自取用峻、缓有别的角度与手段，分别达到挑斡平槫的目的。

我们先看一组数据：

一）青莲寺释迦殿[21]下昂斜率为27/63合3/7；二）王报村二郎庙戏台[22]下昂斜率为3/8；三）下昂斜率为3/9的实例暂时未掌握；四）平遥文庙大成殿、隆兴寺转轮藏头道昂[23]与青莲寺释迦殿耍头均为三举，合3/10；五）隆兴寺转轮藏二道昂约0.275 举，合3/11；六）隆兴寺转轮藏三道昂0.25 举，合3/12……

设以材厚之半 5 分° 作为调节用的基准量A，则青莲寺释迦殿下昂斜率可表述为3A/6A+A、王报村二郎庙为3A/6A+A+A，高平古中庙为3A/6A+A+A+A，平遥文庙大成殿、隆兴寺转轮藏头道昂与青莲寺释迦殿耍头为3A/6A+A+A+A+A， 隆兴寺转轮藏二道昂为3A/6A+A+A+A+A+A， 三道昂则为3A/6A+A+A+A+A+A+A。这些选例的样式差别较大，建成年代也前后悬隔，但其算法均指向一个古老的传统，即遭到李诫批评的“倍斗取长”的原始模数方法。

实际上，倍斗模数制虽不够精确，但胜在算法简单，且最大限度地利用规格化构件控制了空间尺寸的量测，当不同斗件的共用边长与材广趋同（合16 分°）时，以之度量整个建筑最为合宜。由于绝大多数早期遗构的斗栱出跳值倾向于取2倍材广（同时也等同或接近于枓长），因而昂下勾股关系均可藉之化整表达。

这一传统同样影响到了《营造法式》的编纂，虽然握有更加精细、先进的材分模数工具，我们推想李诫还是忠实于下昂以五举定斜的一般传统，在折半法则基础上优先制定了铺作出跳的基本勾股比（昂下每抬高一单材、平出两单材），并以之为起点，继而以半材厚5 分°为基准量逐渐增减跳距（四铺作插昂是唯一减跳的情况）。这样的好处是可以获取随等级增高而趋于平缓的取值序列，产生了自3/5、3/6、3/7、3/8、3/9（实例暂缺）、3/10、3/11直至3/12的整个数组，从而保证下昂斜率可以被灵活调整和简明标记，这是思维逻辑上比例优先的产物，是代数优先于几何的数学传统带来的必然结果。

七、《营造法式》上昂的斜率生成规律

李诫对于上昂的记述不甚均平，在制度“飞昂”条目内极尽详细，但在随后的“总铺作次序”条与功限章节中却了无痕迹，到了图样部分则又突兀地描绘了五至八铺作及平坐用上昂的形象。除却怪异的编排逻辑不论，关于上昂制度本身仍存有三点疑问亟待审查。其一，其施用方式的记载自相矛盾，卷四“飞昂”条称“下昂施之于外跳……上昂施之于里跳之上及平坐铺作之内”，同卷“总铺作次序”条又称“凡铺作并外跳出昂，里跳及平座只用卷头”，则上昂用法及属性难道与卷头相同？其二，下昂的减跳原则简明有序（功限部分的减跳份数虽自行其是，但跳距变化仍极具规律），上昂逐跳跳距的变化却颇为混乱，不同铺数间亦缺乏贯通的法则，那么它的数值是依据什么原理厘定的？其三，功限中明确规定了下昂在补间及转角处的长度，但并未论及上昂，难道它可以被随意调整？若如此又何以“关防工料”？除却这三者外，上昂面临与下昂同样的设计问题，即其自身的斜率应如何取定？而这或许正是解锁上述三个疑点的关键抓手。

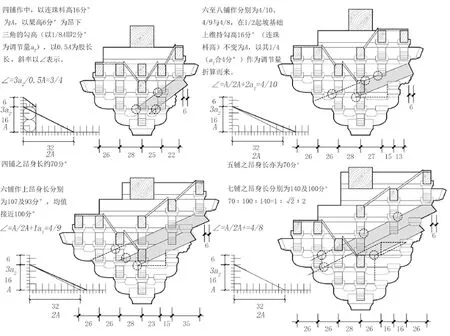
图8：《营造法式》上昂斜率推算方式示意

前文关于《营造法式》下昂斜率生成机制的讨论中，关键的一条原则是昂身的上下边线应交于既有栱、方、枓等构件的外缘或中线等特征点上，以期榫卯设计尽量便于描述而不必完全依赖于现场放样，同一体系下的上昂也理应如此。“飞昂”条原文记称：“二曰上昂，头向外留六分，其昂头外出，昂身斜收向里，并通过柱心……上昂施之里跳之上及平坐铺作之内，昂背斜尖，皆至下枓底外，昂底于跳头枓口内出，其枓口外用靴楔（刻作三卷瓣）”，显然，上昂的下皮线需穿过连珠枓的枓平内沿（偷心造以散枓替代交互枓，但并未说明是否扭转放置，本文仍按进深方向16 分°计），外沿则伸出靴楔以填补昂、枓间空隙。上昂斜率可表示为每抬高连珠枓（上枓完整下枓无耳）16 分°后平出若干份，其取值应符合就简原则，与既有构件的特征点对齐，以下对上昂可能的斜率生成方案进行论证（图8）。

五至八铺作用上昂诸例中，八铺作里跳依次为26、16、16、26 分°，上昂底皮起自第三跳，若将之平移至柱缝处，使其下皮穿过齐心枓底外棱，则头跳26 分°与半个齐心枓长6 分°之和恰与二、三跳之和相等，在表记上昂斜率的勾股中，股长取值定为平出的32 分°，勾高则取连珠枓高16 分°，八铺作斜率为16/32，此时构造节点与构件轮廓间最能保持对位关系[24]。

循此思路，六铺作里转头跳27 分°、二跳推测为15 分°[25]，其一二跳之和与八铺作同为两足材，但连珠枓内移至第二跳头上。仍假设上昂底皮过齐心枓底外棱，则平出40 分°（头两跳之和42 分°+6 分°即扶壁处齐心枓底之半-8 分°即连珠枓宽之半），斜率为16/40，此时上昂上皮恰切过里转瓜栱外侧下棱线。

七铺作里转分别是23、15、35 分°（三四跳之和），连珠枓仍在第二跳上，维持上昂前后构造节点不变，平出值较六铺作减少4 分°，斜率为16/36。

由此，推测的上昂斜率在各铺数间形成数组，六铺作4/10、七铺作4/9、八铺作4/8，昂势随铺数增加依次变陡，勾高恒以连珠枓高为则，股长则以4 分°为率递相增减。

五铺作因不用连珠枓而稍特殊。其里转两跳分别是25、22 分°，上昂下皮线过里转第一杪上交互枓口内沿，抬高平、欹之和6 分°。作图可知，若平出半个斗长8 分°，即斜率为3/4时，上昂上皮线与既有构件间可取得最好的对位关系（昂身在柱缝处恰过齐心枓口外沿，中段过里转慢栱外侧下棱，末端与挑令栱交互枓底内侧下棱相合）。且正如前文所推测的，五六铺作下昂的斜率是3/8，正是同级上昂的一半。实例中，宋端平间（1234—1236 年）复建湖州飞英塔外塔首层上昂的实测斜率约为3/4，恰可作为一个佐证。

八、《营造法式》分级表述上昂斜率的内因分析

前段谈到上昂制度中的三个疑点，关于第一点，即《法式》文本中先申明“上昂施之于里跳之上及平作铺作之内”，继而又称“里跳及平坐只用卷头”的自相抵牾的记述，似乎可以理解为上、下昂应组合使用，否则全卷头造时“若铺作数多，里跳恐太远，即里跳减一铺或两铺；或平棊低，即于平棊方下更加慢栱”，需采用更多的调解措施。上、下昂并用的实例并不罕见，五铺作如日本枥木县镬那寺本堂、六铺作如金华天宁寺，均以上昂斜支下昂后尾。在《法式》体系下，若六铺作上、下昂的设计斜率成立，则不难发现两者取值极度接近，3/8与4/10在较短跳距内抬高值的差异完全可以忽略，此时若将两者组合使用，无疑能在里转部分产生两昂乃至三昂平行延展的意向，获得高铺数下昂造的室内观感，这种对于下昂意向的模仿或许正是《法式》反复阐述上昂的内因。

关于第二个问题，即上昂各跳取值的规律，我们以连珠枓中缝为界，将之拆解为内、外两个部分予以考察。如前所述，六、七、八铺作上昂的斜率变化，是以4 分°为率水平伸缩导致的，这同样是六、七铺作里转第一跳的差值。在河东、晋南一带的宋金遗构中，广泛存在着单材广厚比为1.6 的情况，若认可十进制前提下材厚10分°是先验的，则单材广应视作16 分°（若坚持以材广定材厚，则材厚表述为9.375分°，取值畸零且与材广间比例关系不明显）。此类遗构中下昂与昂形耍头的定斜原则可归纳为“水平方向上以两倍单材广为基准，以材广约数的8、4 分°为调节量相增减，竖直方向上以一单材为抬升量，划定简洁的勾股比”[26]，最终获得整数斜率[27]。16 分°是三小枓的共长，因此这种定斜方法究其实仍源自“倍斗取长”之法，我们认为《法式》上昂制度参照了同一传统。

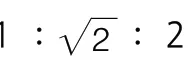
关于上昂的来源，王鲁民曾有过精彩的推测。[28]就《营造法式》语境而论，厘清上昂、挑斡和昂桯间的关系至关重要，朱永春[29]和林琳[30]近来对其做了详细钩沉，笔者亦围绕“又有上昂如昂桯挑斡者”等语句，探讨了昂桯的技术源头问题。[31]《法式》下昂斜率较缓，彻上明造时若欲“于束阑方下昂桯”，仅靠“后尾挑一材两栔或只挑一枓”是无法弥补与下平槫间欠高的，亦即昂桯的斜度必定陡峭，它与远较下昂峻立的上昂一样，应来自于李诫记载的主流匠门之外。昂桯与上昂虽在位置、功用与样式上产生了分化，但存在同源的可能，因而李诫令其互释。

若果如是，则《营造法式》述录上昂无非是以之模拟下昂里转部分的权宜之计，为了在不用下昂（如内柱头）或下昂不可见（没入平棊之上）的情况下，以类似下昂的斜向构件隐喻屋面的存在，上昂造才应运而生，且为了加强斜向态势，刻意令里转大量偷心以露明上昂。也因此，它意在表达的并非基于偏心受压逻辑的“斜柱”（《法式》中斜柱类构件仅剩叉手、托脚与枝樘，且三者均非单材规格），而是通过“错置”“扭曲”与“迁就”的手法折损下昂的挑斡逻辑，转而强行将其嵌入材栔格网以达成减跳目的，并在平棊之下表达下昂伸过柱缝继续上彻屋盖的意向。若里跳只出卷头承托算桯方及其上天花，则下昂必将完全遮蔽，试想厅堂屋架尚且需要借助下昂挑斡平槫以展现构造之美，殿阁又何以能对此全然漠视？下昂既然不能露明，则只能将卷头中的某一跳或两跳转化为与华栱同构的昂形替代品。若非如此，则所谓仅用于金厢斗底槽内槽的上昂，论应用频率尚且低于厅堂中的“昂桯挑斡”，李诫对于后者尚且吝于论述，又何必花费如许之多的笔墨来引介上昂？

九、结论

本文以《法式》所载构件轮廓尺寸的骈合关系为出发点，借鉴若干遗构的实测数据，总结隐藏其中的关于下昂斜率算法的共同规律，进而逆向推导《法式》下昂的斜率取值，并以文本中所列数据为辅证，通过作图验核后得出以下结论：

1.《法式》记载的下昂长度为昂身实长而非心长。

2.《法式》七、八铺作下昂斜率恒为3/11，五、六铺作恒为3/8，四铺作插昂恒为3/5。其操作手段可概括为：在1/2起坡基础上维持勾高15 分°不变，以半材厚5 分°为基准长逐步增减股长调整得来。

3.《法式》文意中的下昂具有固定不变的斜率，下降2—5 分°的规定调节的是华头子对于昂身起算高度的垂直推高值，而非指昂身斜率可以调整。[32]

4.《法式》下昂斜率平缓，因而不具备挑斡平槫的绝对能力，所谓“昂桯挑斡”做法当转借自其他营造体系而非《法式》原生。

5.《法式》下昂里转部分投影长度受限于椽平长，八、七、六铺作下最大的折合份值分别为125分°、120分°与100分°。

6.《法式》上昂斜率从五至八铺作分别为3/4、4/10、4/9与4/8，后三者的操作手段可概括为：在1/2起坡基础上维持勾高16 分°（连珠枓高）不变，以4 分°为基准逐步增减股长得来。

7.本质而言，《法式》上昂仍是对于下昂里转部分的模仿，并非可用于外檐的“斜撑”，且其与“昂桯挑斡”存在同构关系。

8.《法式》上、下昂固定斜率的制定，本质上是“形式优先”的产物，有悖于唐辽以来“结构优先”的传统。下昂折中的出发点是解决斗栱立面形象杂乱的问题，由此衍生的结构缺陷则通过遮椽版和昂桯挑斡做法掩盖解决；上昂则侧重于解决下昂后段于屋内被天花遮蔽，从而不能暗示屋面倾斜态势的问题。

9.《法式》上、下昂斜率算法所凭依的操作原则在更早实例中有大量体现，并非李诫首创。

总之，法式用昂制度体现的复杂性与矛盾性正反映了其编纂过程的曲折与内涵层次的多元，为了保持“飞枊鸟踊”的观感并辅助挑斡平槫，李诫的选择是坚持采用真昂而非假借当时已盛行的平出假昂[33]，他在汇总制度部分时始终致力于将新生的做法理念调和进既有的官式成法中。唐辽以来传统昂制与逐跳计心造作的新体系和外檐横栱密集均齐的新倾向间势必产生矛盾，一时的混融含化终归无法彻底解决问题，随着厅堂化进程的不断加剧，天花之上的部分逐渐露明，下昂尾“随宜枝樘固济”的处理方式终将走向尽头，多方迁就、折中后得出的固定下昂斜率也势必因折下式假昂的普及而失去存在的价值。上述种种都揭示了《营造法式》的制订与颁布恰位于中国木构技术发展史上关键拐点的事实。

注释

[1]梁思成.梁思成全集·第七卷[M].北京：中国建筑工业出版社，2001：381-395.

[2]陈明达.《营造法式》大木作制度研究[M].北京：文物出版社，1993：52-68.

[3]潘谷西，何建中.《营造法式》解读[M].南京：东南大学出版社，2005：92-96.

[4]陈彤.故宫本《营造法式》图样研究（一）——《营造法式》斗栱榫卯探微[M].//中国建筑史论汇刊·第拾壹辑.北京：清华大学出版社，2015：192-233.

[5]“几何问题代数化”系当代建筑史家对于古代工匠思维特征的推测与总结，并不意味着中国缺乏几何传统，只是在营造领域，古人更习惯于以数的比例来指代线条间的相互关系。自《周髀算经》阐述勾股法后，以数理思维解算工程测量问题即成为我国的固有传统，这在《九章算术》《缉古算经》乃至《营造法式》和近世的各类工匠口诀中均有所反映，而与欧式几何体系迥异其趣。

[6]郭书春（主编）.中国科学技术史（数学卷）[M]. 北京：科学出版社，2010：210-216.

[7] 基于各自样式、构造及算法的内在一致性（即技术边界），三种“昂制”类型得以界分，但在理想状况之外，尚存有不少居于过渡阶段的案例，在前述各方面彼此杂糅（如初祖庵大殿样式为“法式型”而构造、算法属“榆林窟型”，保国寺大殿样式与构造为“法式型”而算法属“榆林窟型”，又晋南大量五铺作单昂实例，具体属于哪种类型也取决于如何定义其昂式耍头——它本身符合“唐辽型”的出跳原则，但下随构件为真昂、假昂或华栱时，会导致不同的判定结论），因此只能大致定义其居于哪两型之间。

[8]喻梦哲，惠盛健.唐辽殿阁中下昂的组织逻辑与设计方法述要——以交互枓隔跳现象归平为线索[J].建筑师（录用待刊）.

[9] 文献7中指出佛光寺东大殿檐步架与下昂的勾股弦关系相同，两者为相似三角形。

[10]吕舟.佛光寺东大殿建筑勘察研究报告[M].北京：文物出版社，2011.

[11] 唐辽殿阁铺作中的下昂定斜原则可简单归纳为“每平出一跳下降一足材”，昂身正交于影栱素方并保持上下缘平齐，交互枓隔跳计心归平。当偷心造且内外两大跳等距时，端头必然隔跳趋平，无需额外调整交互枓分位，但在《营造法式》中这套约束条件彻底解体，调节机制灵活化的另一面是定斜原则的多元化和弱化。

[12]文献4。

[13] 《法式》卷十七·大木作功限一“殿阁外檐转角铺作用栱枓等数”记载补间用齐心枓数，八铺作一十二只，七铺作一十只，六铺作、五铺作同为五只，四铺作三只。可知外跳交下昂之横栱上不设齐心枓，昂间实拍密合；而泥道上用者除面宽向需开口以容暗销外，在进深向开口内亦留有宽1.5 分°之隔口包耳，并无抹斜枓平以放过昂身的倾向。

[14] 即便严格按3/11的推想斜率计算，26 分°和25 分°跳长分别折算出7.09 分°和6.82分°垂高，工匠在实际操作时仍会归整到7分°，这与7/25并无区别。

[15] 八铺作中三根斜昂的数据皆自中线量得，其中二昂测值与《法式》记载完全吻合；头昂测值较文本规定短2分°；在子荫深1分°时，三昂测值较中线值恰短2分°，并与原文吻合，其插入扶壁处的深度与二昂对称（类似榫卯做法在解体的高平二仙宫中可以看到）。《法式》分件图样显示，合角昂后尾自尖角向内仍有小段存留，当非贴于转角昂两侧，而是插入扶壁以内。七、八铺作作图结果与记载情况基本一致，但五、六铺作存在瑕疵——文本中的合角昂长度过短（即便视为平长也不够）。但若只从昂上交互枓底外侧量起，则与文本契合，尤其六铺作头昂、二昂同时吻合，这应非巧合，或许与其用于彻上露明造时采用不出昂之“昂桯”并挑斡平槫的做法有关。

[17] 据《法式》“大木作功限一·殿阁外檐补间铺作用栱、枓等数”条记载用下昂数：八铺作三只，一只身长三百分，一只身长二百七十分，一只身长一百七十分。七铺作两只，一只身长二百七十分，一只身长一百七十分。六铺作两只，一只身长二百四十分，一只身长一百五十分。五铺作一只身长一百二十分，四铺作，插昂一只，身长四十分。

[18] 当逐跳昂上交互枓均归平时，铺作外观最为均齐，但在使用真昂的同时却又阻止了跳头降高的诉求，这在逻辑上是自相矛盾的。考察《法式》关于下昂的文意，似乎李诫在遵从结构的自然机制与迁就形式的预先设定之间有所犹豫，最终并未采用能彻底解决问题的平出假昂做法，但作为一种折中手段，放缓昂身终究有损其斜杠杆的工作机制，下昂降高产生的更多问题终归也无法调和，因而假昂的普及终将是无法避免的。

[19] 2—5 分°的极限调整值恰对应于扶壁素方上、下棱的交接位置，这种情况仅在跳距取26 分°时成立。当昂身上下缘对齐到诸如栱方中线这样的特征点时，昂自身的下降份数却往往是畸零的，这或许正是《法式》不对调整值作精确要求而仅赋予一个区间的原因。当不减跳或按功限部分记载减跳5 分°时，头昂自由降跳有助于找到下昂边线与其他构造线（如齐心枓或素方边/中线）的最佳对位关系。就图样而言，似乎六、七、八铺作上交互枓归平也具备潜在的可能，因此《法式》与唐辽官式建筑在下昂制度部分的本质区别在于头昂下伸出露明华头子，在给定的斜率下，可据需要调整头昂高度分位以获得其与扶壁栱方间恰当的对位关系，但这改变不了外跳横栱必与下昂错缝相交的事实。或许李诫载录的《法式》昂制正处于唐辽传统经历革新并走向瓦解的最终环节上。

[20]刘海瑞，张歆.从《营造法式》到《清工部工程做法则例》屋面坡度设计方法比较[J].城市建筑，2013（24）：54-55.

[21]刘畅，汪治，包嫒迪.晋城青莲上寺释迦殿大木尺度设计研究[M].//建筑史（第33辑）.北京：清华大学出版社，2014：36-54.

[22]赵寿堂，徐扬，刘畅.山西高平两座戏台之大木尺度对比研究[M].//建筑史（第42辑）.北京：中国建筑工业出版社，2018：47-69.

[23]刘畅，徐扬，姜铮.算法基因：两例弯折的下昂[M].//中国建筑史论汇刊·第拾贰辑.北京：清华大学出版社，2015：267-311.

[24] 这相当于将上昂先向内侧移动32分°，又因其下皮线需自连珠枓平内沿伸出，将其向外移动半枓长8 分°，此时昂下皮交于里跳第三杪上皮，自交点作垂线向下恰与里跳第一杪上充交互枓的散枓内缘重合。同时，在五举斜率下，第二根上昂上皮恰好同时切过扶壁栱方与里跳慢栱的内侧下棱。

[25] 《营造法式》未记六铺作上昂二、三跳及七铺作上昂三、四跳各自长度，其合计长度分别为28 分°与35 分°。就连珠枓与其内一跳交互枓的间距论，八铺作记为16 分°，七铺作为15分°，六铺作若需择其一为标准，则紧邻的七铺作似乎更为可信（且两者头跳均为奇数，八铺作为偶数）。

[26] 实例如永寿寺雨花宫与少林寺初祖庵的下昂斜率为16/32分°，合4/8；万荣稷王庙为16/（30+8）合0.42举；西溪二仙庙寝殿与龙岩寺中佛殿为16/（32+8）合4/10；南村二仙庙帐龛为16/（32+4+4+4）合4/11。详情参见文献12。

[27]喻梦哲，惠盛健.宋金时期枓栱下昂斜率生成机制及其调节方式研究[M].//建筑史（第45辑）. 2019：近期可确认.

[28]王鲁民.说“昂”[J].古建园林技术，1996（04）：37-40.

[29]朱永春.《营造法式》中“挑斡”与“昂桯”及其相关概念的辨析 [C].//中国《营造法式》国际研讨会论文集，2016：135-144.

[30]林琳.日本禅宗样建筑所见的《营造法式》中“挑斡”与“昂桯”及其相关构件——兼论其与中国江南建筑关系[M].//建筑史（第40 期）.北京：中国建筑工业出版社，2017：241-231.

[31]喻梦哲、惠盛健.华头子斜置现象探析及其与《营造法式》昂桯挑斡关系评述[J].建筑师（录用待刊）.

[32] 殿阁中七、八铺作下昂后尾与平槫间的欠高甚大，仅凭2—5 分°的微调并不能补足空隙，达到令昂尾直接挑斡的目的，反而会令栱、昂间的榫卯交接更趋复杂。若下昂斜率一例一定，则将导致榫卯的开刻位置与深度驳杂无序，这违背了规格化下料的基本需求，对于提高营造效率是极为不利的。绝大多数实例的下昂斜率均为简单整数比，即或如隆兴寺转轮藏逐昂峻缓不一，其斜率还是一组整数列，且反折出的降值亦不在2—5 分°范围内。

[33] 平出假昂在《营造法式》编刻之前已广为流传（如万荣稷王庙大殿、晋祠圣母殿及敦煌三危山老君塔等），在宋画中更是应用于最高等级的皇家建筑（如徽宗绘《瑞鹤图》宣德门城楼），但李诫却未予收录。它的消失亦颇为突然，金元以降，人们甚至宁愿选择更加耗材的折下式假昂作为替代，由此也可看出昂身“应当”斜垂向下的审美观念之强大。