基于调焦-Zernike矩算法的微小零件精确定位研究
2020-11-09张亚军
张亚军
(驻马店职业技术学院,河南 驻马店 463000)
微小零件在食品机械设备中决定了食品加工的质量,例如:饮料灌装设备中的轨迹控制轴承零件保证生产线平稳,使得灌装具有一致性[1]。
传统的微小零件精确定位方法主要依靠人眼以及借助测审理工具找正。但依靠人眼无法连续稳定地进行精确测量[2];找正法虽借助测量工具,但由现场测量来确定零件的正确位置[3],效率低,仅仅适用于单件小批生产。近年来,也有不少学者对微小零件的精确定位方法进行了探究,陈向伟等[4]通过光学显微镜、CCD像机对小型塑料齿轮进行定位,其结果优于人工显微镜测量;Liu等[5]采用几何约束关系法通过动态识别零件间的几何关系,限制零件运动的自由度,沿受约束方向引导零件运动到定位装配位置;谢煌生等[6]利用单目面阵CMOS机器视觉以及图像金字塔的搜索策略和最小二乘法的优化方法,具有较好的实时性和识别率;张习文等[7]采用主动视觉方法利用控制相机的精确运动完成零件的定位,但定位过程中相机需要对零件的特征边缘进行连续跟踪,通过多帧图像的拼接,效率较低,不适于多零件装配的场合;Wang等[8]采用小波插值法来获得图像局部像素信息,并保存该局部规律性到内插图像中,算法重复性好,运算时间短,但检测精度较低,抗噪性能较差;Chao等[9]采用Bertrand曲面法利用图像灰度拟合获取亚像素边缘位置进行定位,抗噪性能好,但曲面模型建立过程比较复杂,适用性不强;Deng等[10]研究表明,Zernike矩亚像素边缘检测算法的检测精度与模板尺寸大小有关,模板尺寸越大检测精度越高,同时检测速度越慢。以上研究都是通过图像比对获取零件的信息,在获取过程中没有调焦或者粗略调焦,导致定位误差比较大。
试验拟采用调焦-Zernike矩算法(Focusing-zernike matrix,F-ZM),建立粗细调焦过程以及Zernike矩精确定位过程,并对微小零件进行定位分析。
1 微小零件定位过程
1.1 调焦过程
1.1.1 微小零件精确定位调焦函数选择 准确运用调焦函数对快速有效地实现微小零件精确定位至关重要,采用粗、精结合的调焦方法,其中粗调焦函数为基于Krisch边缘检测算子[11]。
(1)
式中:
i=0,1,…,7;
j=0,1,…,7;
K(i,j)——中心像素点(i,j)周围8个邻域的像素点灰度均值,取3个相邻点均值与另5个相邻点均值比较,差值较大的作为中心像素点(i,j)的梯度值;
AK——(i,j)点周围8个邻域点中的一个(K>7时,取其除以8之后的余数);
Q1、Q2——权重因子,一般取值Q1=0.78,Q2=0.36。
精调焦采用Sobel算子,评价函数为:
(2)
式中:
K′(i,j)——每个像素的灰度值;
*——卷积运算;

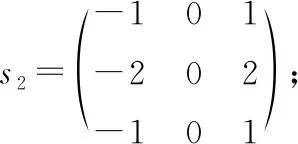
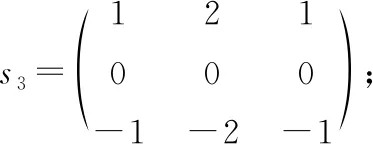
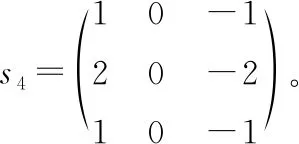
Krisch边缘检测算子的变化幅度平缓,与粗调时电机较大的移动步长相同,无需较高的精度,因此调节速度比较快;Sobel算子变化幅度比较尖锐,与精调时电机较小的移动步长相同,精度较高。
1.1.2 调焦窗口动态选择 实时性是调焦的重要特征之一,采用动态调焦窗口可保证算法的运行时间降至最低[12]。首先以目标区域(m,k)为中心,向外扩展p个像素,从而获得新的调焦窗口,其中新调焦窗口左边界为L,L=mmin-p,mmin为目标区域左侧最小值;R为新窗口右边界,R=mmax+p,mmax为目标区域右侧最大值;T新窗口上边界,T=kmin-p,kmin为目标区域上侧最小值;B为新窗口下边界,B=kmax+p,kmax为目标区域下侧最大值。则新窗口的像素总数P为:
P=(R-L)·(B-T)=(mmax-mmin+2p)·(kmax-kmin+2p)。
(3)
增设调焦窗口修正因子q修正因目标变化对调焦清晰度评价函数的影响:
q=1/(PInP),
(4)
式中:
1/P——获取调焦窗口内调焦图像的平均清晰度;
1/InP——调焦权重。
只有在1/P和1/InP同时具有最大值时才能够获得最佳调焦结果。
1.1.3 搜索焦点策略 为了克服经典爬山搜索算法的缺陷,在同一方向上采集3帧图像,并将第3帧图像与其前面相邻的2帧图像作为初始拟合点[13],对应的调焦评价函数值分别为K1、K2和K3,搜索评价函数的第一个“下坡点”,设阈值δ,文中设定δ=0.5,若K1≤K2≤K3≤δ,则此时在爬山阶段,方向和步距不变;如果出现K1>K2且K2≤K3≤δ的结果,则说明在调焦过程中受到噪声干扰,此时必须往该次搜索方向进行搜索;若δ>K1>K2>K3,说明此时位于爬山的下坡区域,如果该点是第一个“下坡点”,则以其前的两点作为初始拟合点。
1.2 改进Zernike矩亚像素边缘定位
1.2.1 Zernike矩亚像素边缘定位过程 由于微小零件定位精度要求高,像素级边缘检测定位不能满足需求,应进一步提高边缘定位精度,通过Zernike矩进行亚像素边缘定位,能够满足精确定位需求[14-16]。设图像f(x,y)的Zernike矩为:
(5)
式中:
Znm——n阶m次Zernike矩;
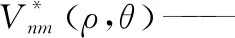
建立图像的理想阶跃边缘模型参数:k为阶跃高度,h为背景灰度,l为圆心到边缘的垂直距离,φ是l和x轴的夹角。如果将边缘旋转-φ,则边缘与y轴平行,则:
(6)
式中:
f′(x,y)——图像旋转后的边缘函数。
通过标准矩来归一化图像,则图像的理想阶跃边缘模型的3个边缘参数为:
(7)
式中:

Z——Zernike的未旋转矩;
k——阶跃幅度;
h——图像背景灰度;
l——圆心到边缘的垂直距离,mm。

(8)
式中:
(xs、ys)——以(x、y)为卷积窗口中心求得的亚像素坐标值;
(x、y)——单位圆的圆心坐标值;
φ——以(x、y)为卷积窗口中心求得的实际边缘与x轴方向的夹角角度,°。
1.2.2 基于目标点归一化的最大外接单位圆确定 找出定位零件的形状质心O(xo,yo),再利用欧式距离找出零件上距离形状质心O最远的像素点B(xb,yb),半径为:
(9)
把所有的目标点归一化到单位圆内,这就使得得到的Zernike矩具有平移和尺度不变性。计算出零件图像的0阶0次几何矩:
(10)
计算单位圆中n阶m次的Zernike矩:
(11)
利用0阶几何矩归一化Zernike矩:
(12)
最后在像素点(xs,ys)左、右各取一个最近的像素点(xs1,ys1)、(xs2,ys2)进行卷积,P1、P2是以点(xs1,ys1)、(xs2,ys2)为中心的卷积窗口矩阵,获取点(xs1,ys1)、(xs2,ys2)的n阶m次Zernike矩的差值:
(13)
式中:
N——Mnm模板的大小;
Mnm——Zernike矩的模板;
(i,j)——模板数。
文中要求Dnm<0.000 16即可满足定位。
2 试验仿真
计算机配置为:内存8 GB,CPU为Intel i5-9600k处理器,主频3.7 GHz;程序由Matlab7.0编写;试验装置主要由显微成像系统和图像处理系统两部分组成,通过1394接口卡连接,以保证图像数据实时传输。
2.1 Zernike矩奇、偶模板对比
规则形状和不规则形状零件如图1所示,Zernike矩算法、调焦-Zernike矩算法的5×5、3×3奇模板和4×4偶模板进行微小零件定位分析对比如图2~4所示。
从图2~4可以看出,模板的数量影响定位误差,在规则形状对比分析结果中奇模板3×3模板比奇模板5×5模板、偶模板4×4模板定位误差大,偶模板4×4模板比奇模板5×5模板定位误差大,同样不规则形状也是模板数越多定位误差越小;模板数相同的情况下,规则形状比不规则形状的误差小。这是因为Zernike矩模板数越大,Zernike矩的差值越小,定位精度越高。

图1 零件图形
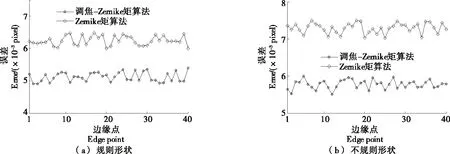
图2 3×3模板对比分析结果
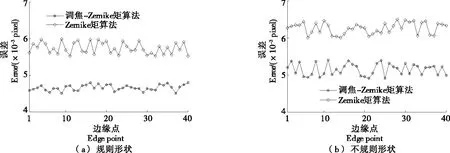
图3 4×4模板对比分析结果
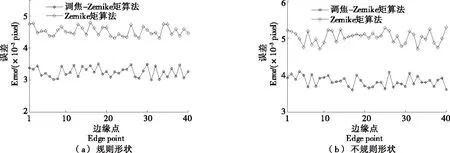
图4 5×5模板对比分析结果
2.2 移动定位分析
通过两个微型金属圆柱腔的自动对准和堆叠的微装配任务来分析算法的性能,装配任务要求移动的微型金属圆柱腔对准非移动的微型金属圆柱腔期望的方向,两个微型金属圆柱腔的中心轴线必须精确对准,采用摄像机所拍摄从离焦到调焦条件下采集的零件图像系列如图5 所示。
首先获得2帧模糊的图像,如图5(a)和(b)所示;利用成像系统传递函数(Modulation transfer function,MTF)来评价调焦图像,MTF值越大,调焦图像质量越好。从图5(a)和(b)估算出目标体的清晰度,确定调焦方向,调焦电机完成调节镜头的微小零件精确定位,由于获得帧数的过程中伴随着变倍调焦,使得获得图像的清晰度变化明显,当调焦至正焦位置时,获得如图5(c)和(d)的结果,第8帧时获得调焦图像结果如图5(e)所示,图5(f) 为最佳效果。

图5 调焦过程
MTF计算为:
(14)
式中:
MTF——成像系统调制传递函数值(值越大表征图像质量越好);
Imax——最大亮度;
Imin——最小亮度。
离焦程度越大,图像越模糊,MTF曲线下降越快。
调焦-Zernike矩算法、Zernike矩算法对微型金属圆柱腔目标调焦MTF归一化值如图6所示,每种算法各进行蒙特卡罗21次试验。
从图6可以看出,调焦-Zernike矩算法的MTF值比较大,可有效避免调焦评价函数值局部的波动性,提高调焦精度,同时使得结果更加稳定,不但提高了搜索效率,而且避免因清晰度评价函数出现局部峰值点而发生误调焦现象。
对准过程如图7所示。
在完成对准状态过程中利用纳秒脉冲激光,采用相同的加工速度和激光参数,改变x、y轴方向的位置,获得重叠区域一系列变化的阴影面积,图像品质等于移动金属圆柱腔阴影面积除以非移动金属圆柱腔阴影面积,即完全重叠则图像品质为1。图像品质的变化情况如图8所示。
从图8可以看出,调焦-Zernike矩算法比Zernike矩算法的图像品质要大,且接近于1,即获得图像最清晰。
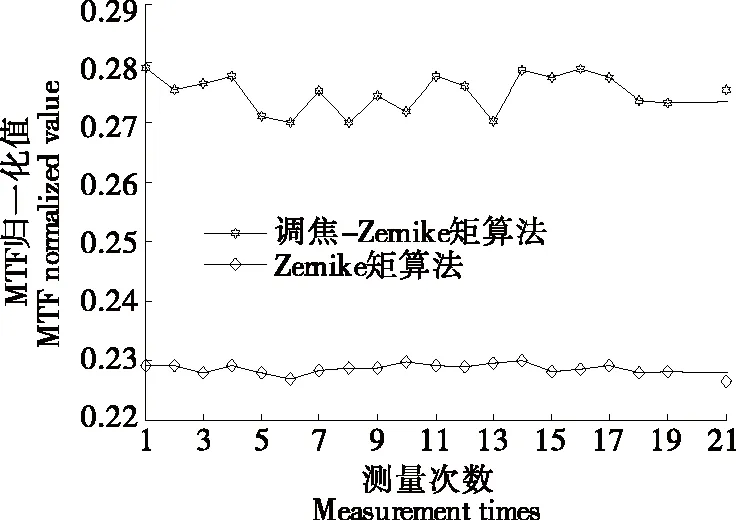
图6 MTF结果

图7 对准过程
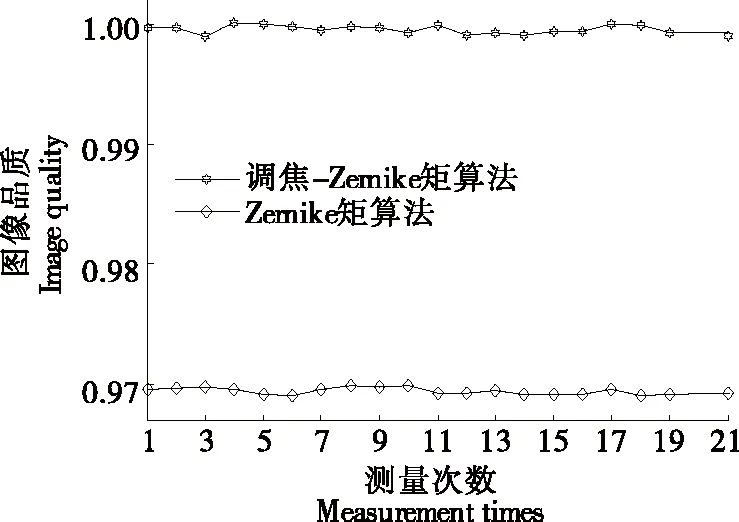
图8 图像品质变化情况
2.3 定位误差分析
在对准过程中,需要对非移动的微型金属圆柱腔坐标定位分析,圆心在(74.000 0,74.000 0),半径为34,通过MV-3000FC型号高性能工业检测专用相机随机获得10个实际边缘坐标,每获取一个实际边缘坐标,调焦-Zernike矩算法进行一次亚像素边缘坐标定位计算,最终检测结果如表1所示。
对表1中的实际边缘坐标数据依次进行人工法、找正法、几何约束关系法、CMOS机器视觉法、主动视觉法分析,与调焦-Zernike矩算法相比结果如图9所示。
从图9可以看出,调焦-Zernike矩算法的定位绝对误差x方向最大值为0.032 5像素密度,y方向最大值为0.032 1 像素密度,误差相比其他方法较小,说明调焦-Zernike矩算法定位精确度较高。

表1 亚像素检测结果
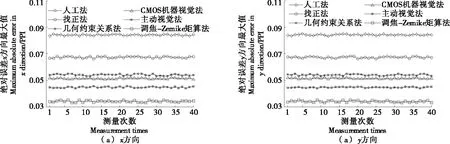
图9 绝对误差最大值相比结果
3 结论
(1) 针对微小零件尺寸检测过程中存在的问题,试验提出一种基于调焦-Zernike矩算法的微小零件尺寸检测方法。通过粗、精调焦函数以及爬山算法改进解决了Zernike矩算法运算时间较长的问题,缩小了Zernike矩的计算范围,使得调焦-Zernike矩在零件定位精度提高的情况下,缩短了计算时间,提高了速度。
(2) 在微小零件尺寸检测中,存在像素级边缘定位不能满足实际工作需求的缺陷,采用改进Zernike矩算法能够获得图像的边缘位置,大大地提高了检测精度。
(3) 试验只是针对规则的微小零件进行检测,并未对不规则的微小零件进行检测,这将是今后研究的一个方向。
