微量混合粉状颗粒称量系统设计
2020-11-09侯达盘刘菊东
侯达盘 刘菊东
(集美大学机械与能源工程学院,福建 厦门 361021)
随着食品工业的发展,散状物料的定量准确度和定量速度都能达到满意的结果,但是对微量粉状颗粒的保健食品和药品等贵重物料的定量却不尽人意,特别是混合均匀后的多种粉状颗粒散物料进行自动定量称量充填技术。目前对精度要求不高的食品行业可以采用容积法定量和称重式定量对混合粉状物料进行称量,但对于保健品、药品等贵重食药品行业,其准确度还不能满足使用要求。周丹等[1-2]提出采用螺杆输送和混合式加料进行粉体填充,但此方法存在两个缺陷:① 螺杆在旋转驱动混合颗粒向前进给过程中,物料受螺杆表面摩擦力影响,及不同性质颗粒相互作用频繁使得运动形态复杂容易导致混合物出现物料分层现象[3-4],不能保证产品的混合均匀性;② 混合式加料采用初次加料称重后进行补料,微量称量的二次补料量极小,存在一定误差,在生产中难以实现。为解决准确、均匀定量的问题,研究拟提出一种基于容积法的组合计算过程,采用容积法对粉状颗粒初次定形定量,通过对定容物料组合计算过程的问题进行研究。
1 称量方法选择
目前,传统的粉状颗粒的计量方式主要有两种,容积法和振动给料称重法。这两种方法各有优缺点和不同的应用条件,容积法计量速度相对较快,但误差较大,需要对物料的堆积密度保持稳定,微量称量过程中误差很难控制在合理范围。振动给料称重法精度很高,但是因为混合物料的颗粒密度的不同,在振动过程中会对颗粒混合均匀性产生影响,振动幅度越大、时间越长,混合越不均匀[5-7]。通过微量组合系统可以快速地提升准确度和称量速度[8],其主要特征:① 采用容积法定型保证物料的均匀性和快速定量;② 容积法称量后采用小型称重平台对产品进行准确称量;③ 通过计算得到较精确的组合,保证称量目标值的准确度。
2 微量混合粉状颗料称量系统的设计
容积式的称量法在微量定量过程中会产生一定的误差,量越小,误差的比例就会越大。称量后,通过3~5斗的组合可以将误差控制到很小的范围[9-10]。
2.1 定容积称量方式的设计
设计合理、制造和装配精良的容积计量系统,以及稳定的物料堆积密度,通过调试可以保证大部分计量在较小的误差范围内。快速的容积计量可达到提高计量速度的目的,称重校核可获得准确的计量数值。
利用混合颗粒为固态的特点采用定容式如图1所示,首先制造与成品横截面相同的高精度模具。送入较多的混合颗粒,填满模具型腔后,型腔压板微向上顶促使颗粒成型,移动台后撤将多余部分去除,型腔压板将物料顶出,由移动台向前将成型颗粒推入称重台,同时进行第二次加料。称重台对物料进行校核,误差越小越有利于组合。
定容成型后,物料经过称量得到准确的质量ti,再经过计算机组合得到最佳组合单元,如图2所示,称重单元向下投料到模具空腔,在成型、称量、投料过程中物料始终保持结合成型状态,所以不会产生分层现象。经过第二次的挤压、成型后,形成最终成品。
2.2 组合过程对称量准确度的影响

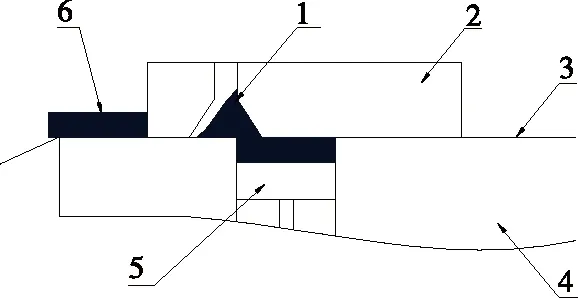
1. 混合颗粒 2. 移动台 3. 导向面 4. 基座 5. 型腔压板 6. 物料成品
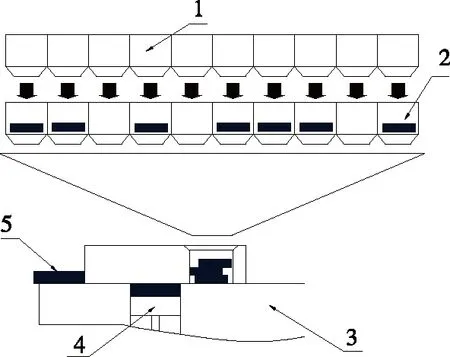
1. 定容成形器 2. 称重单元 3. 基座 4. 型腔压板 5. 物料成品
即合格质量要求在(T-ε,T+ε)之间,Pi为一次定量组合合格的概率[11]。
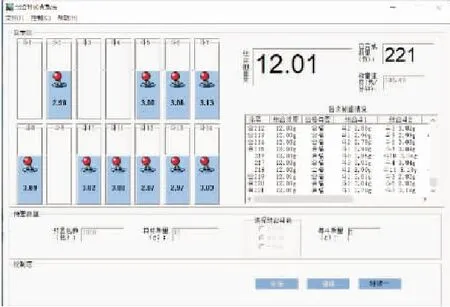
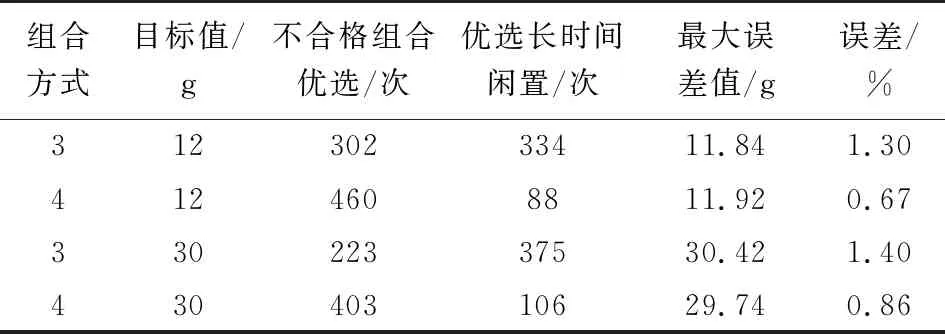
P{T-ε< P{-ε< (1) 假设合格组合概率为P,则不合格组合的概率为1-P,x次组合中连续不合格组合的概率为(1-P)x,则x次组合中的合格组合概率为 Pi=1-(1-P)x。 (2) (1) 根据式(1)要增大Pi采用增大定量允许误差为±ε受到准确度要求限制,必须减小每次参与组合数量m和减小定容物料每次定容质量分布的标准差σ。而组合数量m过小时,不利于组合成功。 所以要得到较好的合格率Pi,必须减小每次组合时单个定容物料的标准差σ。 每个斗的质量是按正态分布N(u,σ2)随机产生的,如果大部分误差都大于u,在组合过程中有可能某一次所有的质量组合都不合格;选用称量斗时优先选用误差较小的进行组合,可能产生某一误差较大的斗一直未被选用,必须采取一定的措施进行解决。 组合秤采用n个单元斗随机组合,每次组合随机找取最接近目标值的组合。因此,各单元斗不能均匀使用,某一个单元偏大或偏小就有可能长时间未被选用,造成长时间闲置的问题。同时相应的称量传感器就长期得不到零位的调整而降低称量准确度。这样就不能使该单元得到充分利用,无法将组合秤的功用发挥至最佳。 鉴于以上问题,必须要尽量保持各单元使用均匀。在不影响称量结果的前提下,当某个单元长时间未被选到时,应该首先选用该单元。综合考虑了单元的数目以及组合单元的数量,设定当某个单元连续8次未被选用时,首选该单元。 假设14个斗中的m个被选为了上次的组合,在这次组合中清为零,剩下14-m个斗。如果这14-m个斗中有7个以上的斗质量都大于每斗标准质量的(100.0%+0.5%)或者都小于每斗标准质量的(100.0%-0.5%),就出现了多个单元斗质量一齐偏大或一齐偏小的现象,这就造成在后续组合过程中有较大的概率产生不合格的情况。 因此在此处进行判断后,为了尽可能防止最终结果不合格,需采取措施。如果判断为有较大的可能性不合格,达到了检测标准,则在对上次为零的料斗加料时控制加料量,使其中某一个斗的加料量为原标准值的100.0%-3×1.5%(检测时质量偏大)或100.0%+3×1.5%(检测时质量偏小),然后在下次组合时优先选用该斗以消除有过多的单元斗不合格的情况,从而最大限度地避免不合格组合的出现,组合过程见图3。 对于组合斗数为3的情况,11个斗中是否有7个以上斗的质量不合格,特殊加料量为标准值的100.0%-2×1.5%(检测时质量偏大)或100.0%+2×1.5%(检测时质量偏小)。若组合斗数为5,则考虑剩余9个中是否有5个以上斗的质量不合格,特殊加料量为标准值的100.0%-4×1.5%(检测时质量偏大)或100.0%+4×1.5%(检测时质量偏小)。 图3 组合过程的流程图 为了测试该方法是否有用,进行仿真试验。试验进行1 000次组合,组合斗数分别选用3、4斗。 从表1可知,采用此方法大大降低了不合格率。各个范围内的质量,采用不同的组合斗数,合格率都比较高。反观不采取任何措施时,不合格率明显很高,特别是在称量范围大于100 g的情况下,不合格率偏大,存在称量效率降低,不符合生产要求。由此可见,预防措施有效,并且在实际控制中也比较容易实现,只需调整下模具的型腔空间即可。采用此预防措施可以较大限度地避免不合格组合的出现。 依据某型混合机对多种粉状药物进行混和后,在模具腔内定容成型后得到的重量ti,对实际的组合过程,仿真流程: 采用正态分布产生n个随机数,仿真n个称料斗质量ti(i=1,2,3,…,n)。组合计算可能的组合质量Ti(i=1,2,3,…,r)。根据目标质量T和上下限±ε判断Ti是否合格,将与均值相差最小的r个斗中的物料组合并标记。如图4所示,斗1、3、4、9被选中组合得到目标质量12.01 g,余下的10个斗进行组合选中一个最佳组合,将组合完的空置斗1、3、4、9按照正态分布生成新的随机变量,按照图3组合过程。继续下轮组合。若某斗中物料连续8次没有参与组合,则优先选择与其他斗组合。重复2组试验,每组进行1 000次仿真组合,设目标值为实际应用的12 g和30 g两种情况。仿真如图4所示,左边显示的是每个斗物料的质量,右边显示出每次的最佳组合和组合最终质量Ti。 分别对3单元和4单元两种情况进行仿真,其他参数和组合结果如表2所示。 通过仿真可以发现:预防不合格组合过程中优选某一单元的次数较多,最高达到46%,主要剩下的单元为10,设定的偏大或偏小单元数为7,总容量较小,所以出现的概率较大;微量组合(30 g以下)的误差值较小,最大误差1.4%,符合生产的使用要求(±1.5%)。 表1 采用预防措施与否的合格率 图4 组合过程的仿真图 表2 计算机仿真结果 (1) 在采用容积式定量填充的情况下,可能获得的定量是一个随机数,受到密度变化、定量过程速度和压力的影响可能产生较大的误差,通过组合后,所获得的称量较为靠近目标值。 (2) 采用定容成型再组合称量,全过程物料保持成形状态,可以避免物料的分层,保持物料的混合均匀性。 (3) 组合的包数越多,出现闲置斗的可能性就越低,最大误差相对较低,出现合格组合的概率更大。对于贵重食药品的物料具有较好的应用价值,可以将误差控制在较小的范围,同时又能准确定量代替人工或容积法称量。 随着食药品工业的发展和传感器技术的发展,微量称量组合计算的精度会越来越高,目前研究的称量质量还有向微量化发展的趋势,下一步的工作需要在系统组合计算过程中的算法方面和称量过程的系统设计作进一步研究。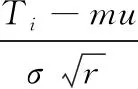
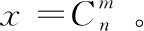

3 组合称量过程中存在的问题及解决办法
3.1 避免某个定容单元长时间闲置的方法
3.2 避免出现不合格组合的措施
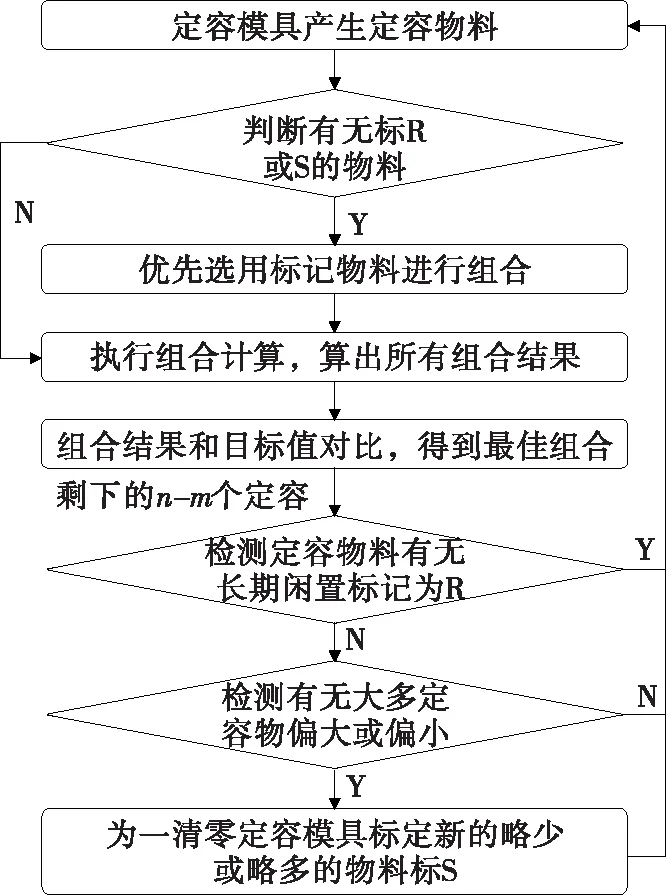
4 计算机仿真及结果

5 结论
