简化双山体风压干扰效应的数值模拟
2020-11-07张守领
张守领
(淮北职业技术学院 建筑工程系,安徽 淮北 235000)
我国国土面积有近70%是被山区、丘陵等复杂地形地貌所覆盖﹒复杂地形处山丘起伏,沟壑纵横,在高山峡谷间容易形成山谷风等效应﹒与平坦开阔地区相比,复杂地形的风场特性有很大不同﹒对复杂地形开展了深入且系统的研究,将对结构风荷载评估、污染物扩散预测、风力发电机选址等大有裨益﹒使用简单规则的山体模型研究复杂地形具有试验精度高,规律经验易于总结等优点﹒
国内外对于简单规则地形模型的研究较多,Kim 等[1]分别用风洞试验与数值计算的方法研究了单个山体与连续双山体上的流动特性,测量了平均速度剖面、湍流特性和表面压力分布﹒Miller等[2]指出一些风荷载规范过于简单的评估地形对于设计风速的影响,用简单连续正弦型山体模拟其周围地形,考虑了二维复杂表面边界层流动的风洞研究结果,对上游地形的影响进行了量化﹒Takahashi 等[3]研究了截面为余弦平方型山体上的 湍流流动,发现明显的加速度不仅发生在山顶,还发生在山体另一侧的斜坡中间位置处﹒Carpenter 等[4]测量了浅正弦山体等多个不规则山体在内的多种地形的平均速度和纵向湍流,发现单个缓坡正弦山丘的峰值风速最大﹒Lun[5]对2种常见的地形特征,即悬崖和小山,进行了二维数值模拟,研究了这些模型在预测流场特性方面的性能﹒李正良等[6]为了研究平均风速与脉动风速在复杂山地中的分布规律,进行了不同山体间隔距离、不同遮挡山体坡度和高度的复杂三维山体模型边界层风洞试验﹒楼文娟等[7]采用风洞试验与数值模拟相结合的方法,研究典型山地地形竖向风速的大小与分布﹒研究发现在1/3 山高以上的迎风坡位置应当考虑竖向风速,且在山高与山底直径之比大于1︰5 时,需要考虑山顶位置的竖向风速﹒
对于简单规则山体风场特性的研究,国内外学者大多关注山体之间的加速效应,而对于山体表面风压分布研究较少﹒本文针对简化双山体风压分布问题,采用CFD 数值模拟方法,研究双山体的平均风压系数及其干扰效应﹒
1 二维山体模型
1.1 山体模型
目前对于山体形状的选取,主要有钟形、高斯形、余弦平方形等﹒过多地在意山体形状对于研究复杂地形处风场特性意义不大[8]﹒本文选用的山体为余弦平方形,见图1﹒
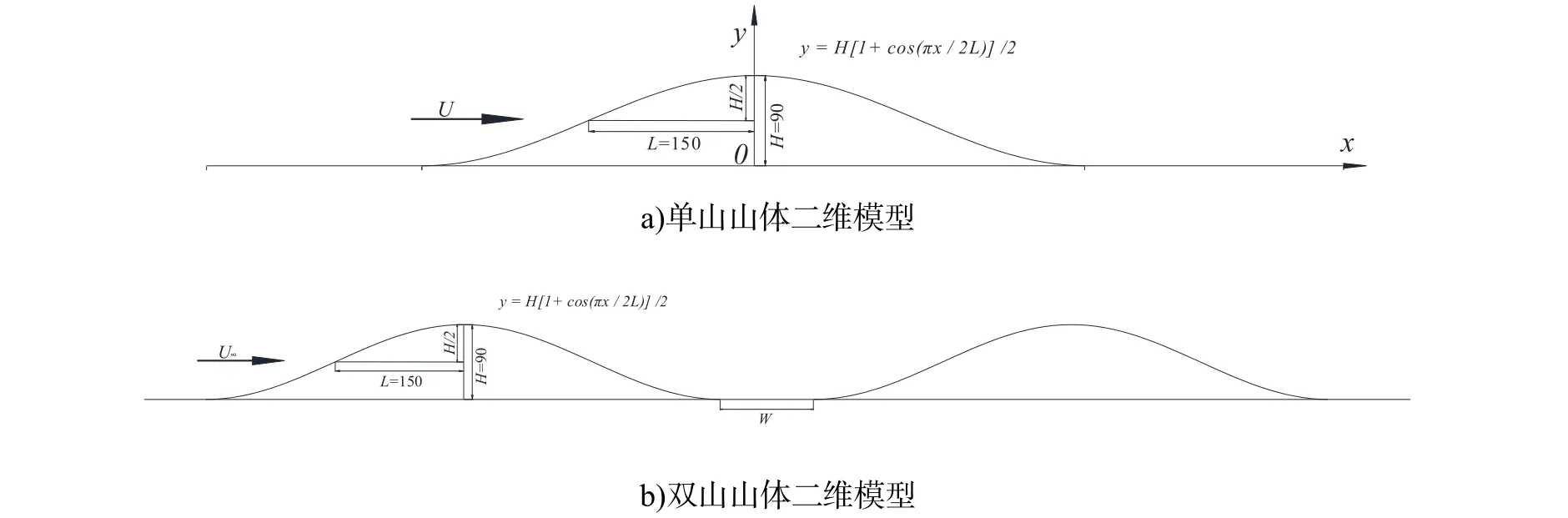
图1 简化的二维山体模型
1.2 单山模拟对比
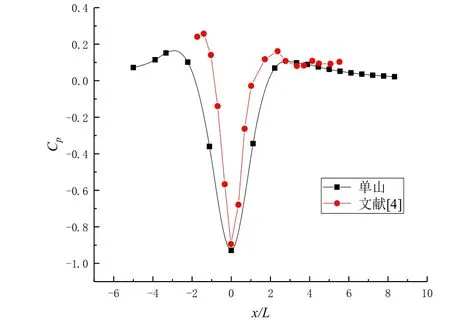
图2 数值计算与文献结果对比
首先,进行单山体模拟,主要目的有2 个:一是将模拟结果与已有文献中的结果进行对比,在保证数值方法和计算结果正确的前提下进行双山体模拟;二是将单山体的计算结果作为参考依据,与双山体试验结果进行比较﹒本文用平均风压系数来描述山体周围风压的变化,在相同坡度的山体模型以及本文的数值计算方法下,由图2 发现,山体表面平均风压系数计算结果与文献[4]大致相同,计算结果显示山顶后未见流动分离的发生,符合文献[4]无扰动发生的结论﹒说明本文采用的数值方法和模型可运用到双山物理模型中,研究其相互之间的干扰效应﹒
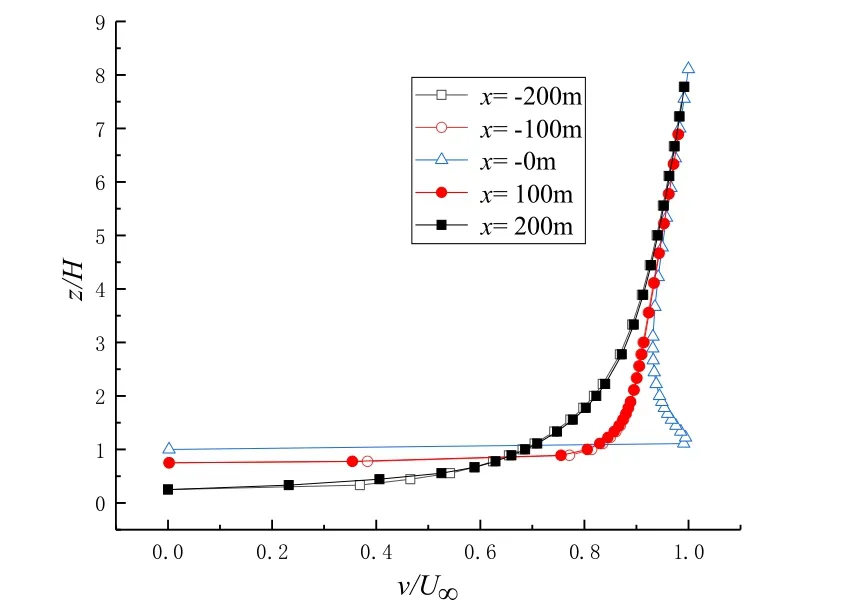
图3 单山山体风速随高度变化
图3 为单山体山上的5 条监测线的平均风速 剖面图﹒其中,z 为监测点离地高度;H 为山高;v 为监测点实测风速;U∞为最大来流参考风速﹒图3 中风速与高度均无量纲处理,不难发现:山体的结构对称,山两边对称位置处的风速变化曲线也基本一致,山顶的近地面风速明显增大,这和文献[4]中总结的山顶风速增大的规律相同﹒
2 数值计算
本文采用CFD 数值计算的方法模拟双山之间的干扰,计算需要满足流体力学3 大守恒方程,即质量守恒、动量守恒和能量守恒方程:
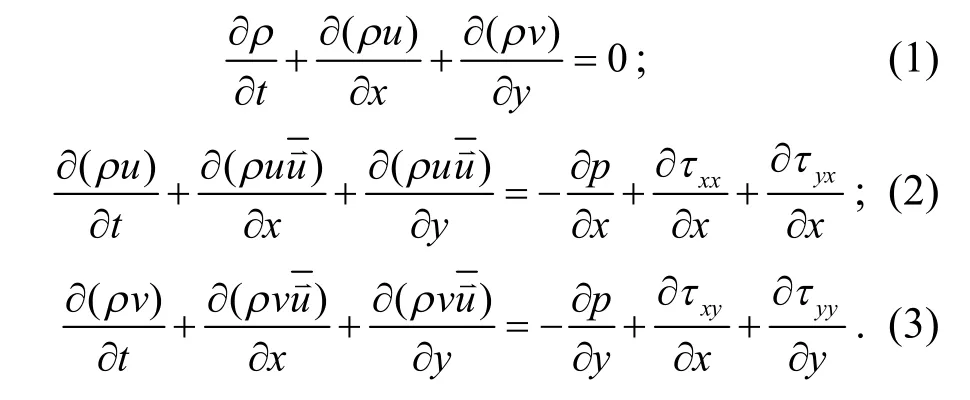

图4 网格局部加密
采用流体力学Fluent 软件进行数值模拟,边界取定的计算域及湍流定义可参考文献[9],前方长度取1 000 m,后方取2 000 m,纵向高度取1 000 m﹒模型网格划分在ICEM 中进行,采用非正交网格,在近山体表面的网格进行了二次加密,经测试网格质量满足要求,见图4,网格总数10 万左右﹒地面和山体设为壁面,出口设置为压力为0 的压力出口边界,采用Realizable k-ε 湍流模型,非定常计算,时间步长为0.5 s,迭代1 500步,计算域离散采用SIMPLE 方法﹒速度入口边界使用UDF 自定义函数模拟B 类风场,设定风速初始值为30 m/s﹒由于本文对风压的干扰采用无量纲研究,因此该初始风速对本研究无影响﹒ 测点横坐标布置如表1 所示﹒纵坐标监测有规律布置:在100 m 高度内,间隔10 m 布置监测点;在200 m 及以上间隔20 m 布置监测点﹒

表1 单山体监测点横坐标 m
3 参数定义
3.1 平均风压系数定义
可用无量纲的风压系数来描述山体上风压分布情况,风压系数定义如下:
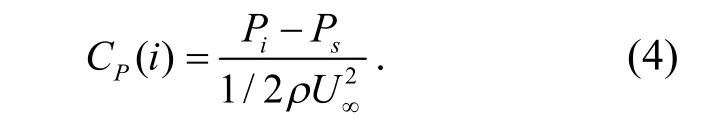
式中,Pi是山体表面某监测点处测得的瞬时压力值;Ps是参考点的静压值;ρ 为空气密度;U∞为风速﹒
平均风压系数Cp, mean可定义为:
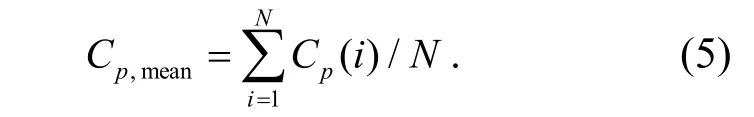
式中,N 为计算模拟布置的监测点数﹒
3.2 双山体干扰因子定义
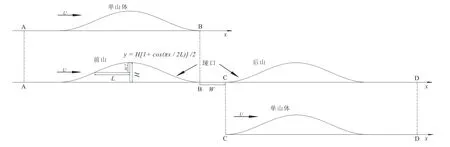
图5 单山、双山模型及其区域划分
双山体模型及山体参数如图5 所示,前、后 两山形状与单山体完全相同(H=90 m,L=150 m),等效坡度均为0.3﹒为方便阐述单山与双山相对位置处的干扰效应,将单山、双山划分为AB、BC 和CD 3 段,两山间隔(BC 段)称为垭口﹒本文通过改变垭口的宽度W 来研究单山、双山风压系数的干扰效应﹒
如图5 所示,将双山体前山AB 段各测点平均风压系数与单山体AB 段各测点平均风压系数进行比较,AB 段测点共216 个;将双山体后山CD 段各测点平均风压系数与单山体CD 段各测点平均风压系数进行比较,CD 段测点共384 个﹒为量化对比大小,定义平均风压系数干扰因子I:

4 双山体平均风压干扰效应
对于双山体的研究可分为前山、后山和两山之间的垭口3 部分﹒前山与单山对比,后山及其尾流区与单山及单山尾流区对比,这样可以充分说明前山对后山、后山对前山以及前山对后山尾流区域的相互干扰﹒
为了更好地描述干扰现象,对AB、CD 段进一步划分,定义前山山顶前为Ⅰ区;山顶后为Ⅱ区;后山山顶前为Ⅲ区;山顶后为Ⅳ区,见图6﹒其余情况的双山间隔分区也按此原则分类﹒由图6可以发现:AB 段Ⅰ区、Ⅱ区干扰系数等值圈出现在山体的左右两边斜向上45°处,等值线上的系数最大为2,即在Ⅰ区山体前方200 m,高度300 m 处﹒其余位置的等值线数值不大,可等同单山考虑,虽后山对前山有一定的干扰,但影响不大﹒CD 段Ⅲ区内的干扰现象显著,在上底的垂直高度300 m 时干扰系数最大可达2.5,200 m 以内的等值线数值较小,等值圈分布密集,前山对后山的迎风面影响较大;Ⅳ区的干扰效应不明显,在山顶后水平距离400 m 高度200 m 内干扰系数为1.5,之后无干扰现象,前山对后山背风面之后也无干扰影响﹒综上,双山间隔为0 m 时干扰现象不显著,可视为单山考虑﹒
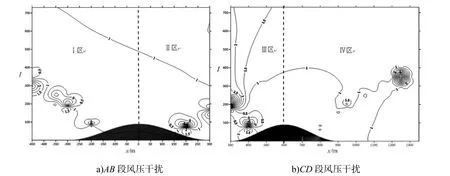
图6 间隔W=0 m 风压干扰等值线
图7 是间隔W=30 m 时两山之间的风压干扰图﹒Ⅰ区、Ⅱ区内干扰系数在高度300 m 内最大,达到6,说明风压提高了5 倍,后山对前山干扰较大,其余区域大多为2~4 倍的影响﹒干扰方向与上一间隔相同,都为山左右两边的45°方向﹒观察Ⅲ区,高度300 m 内最大,达到6,随着高度的增加,干扰等值线数值也越大﹒100 m 高度内有部分呈负数,后山的迎风面出现负压区,表现为吸力,前山对后山的影响不容忽视﹒Ⅳ区内在高度400 m 内干扰等值线呈螺旋状向右斜上方发展,包括的范围也较广,最大干扰系数为5﹒与单山相比,在双山间隔为30 m,高度400 m 内,4 个区域的干扰系数都较大,有3~4 倍的干扰现象发生﹒
图8 和图9 分别为间隔60 和90 m 时两山之间的风压干扰图﹒通过观察可以发现:该2 种间隔下的干扰现象与间隔30 m 时的干扰现象基本相同﹒Ⅰ区在高度300 m,前山山顶前450 m 干扰最大,达到8,越靠近山体,其干扰因子逐渐减小,等值圈分布方式与之前的工况相同﹒Ⅱ区的干扰相比Ⅰ区较小,在山顶后水平距离100 m高度100 m 时出现负的干扰现象,说明垭口处出现回流,后山对前山背风面的影响较大﹒观察Ⅲ区,2 图曲线基本一致,干扰圈相对密集,前山对后山的干扰在300 m 高度内最大,达8 倍﹒2图Ⅳ区的现象和图7 类似,在高度400 m 内最大干扰因子为5,干扰等值线平均数值都大于在30 m 间隔下的干扰﹒综上,间隔60 和90 m 时两山之间的干扰现象更为严重﹒
图10 为W=120 m 两山之间的风压干扰图﹒由图10 可以发现该间隔下的等值线图明显区别于前4 个工况﹒图中的干扰因子普遍较小,两山间隔120 m 时干扰效应减弱﹒
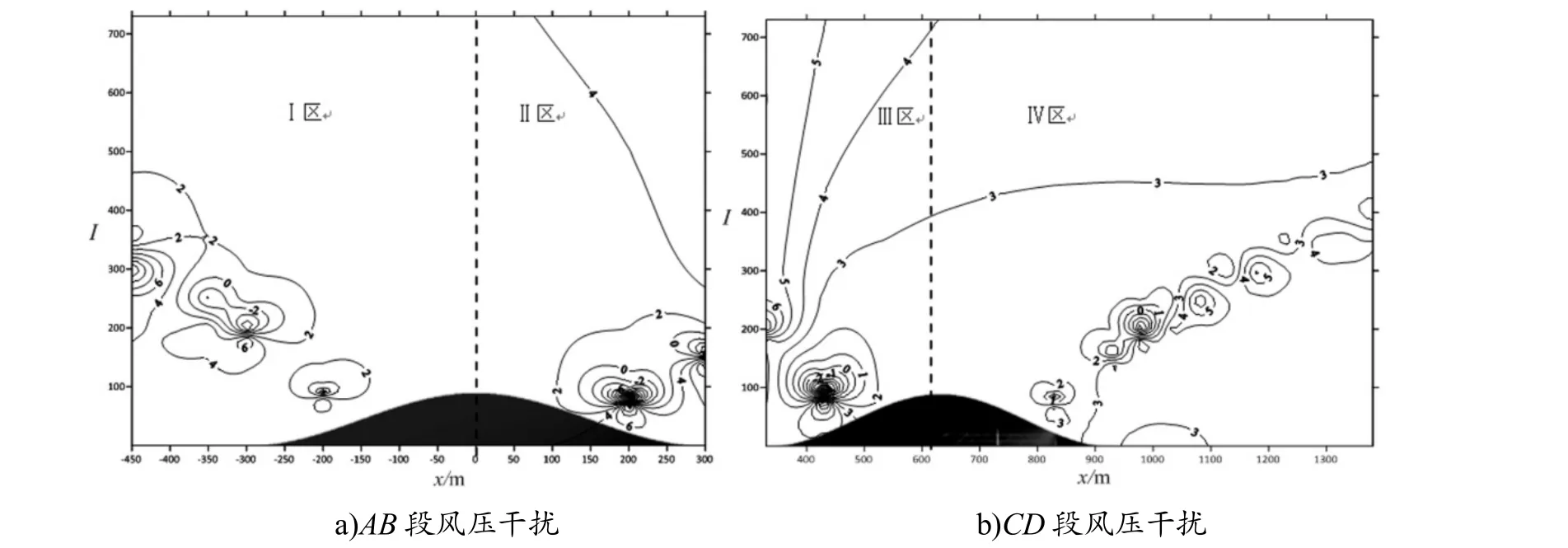
图7 间隔W=30 m 风压干扰等值线
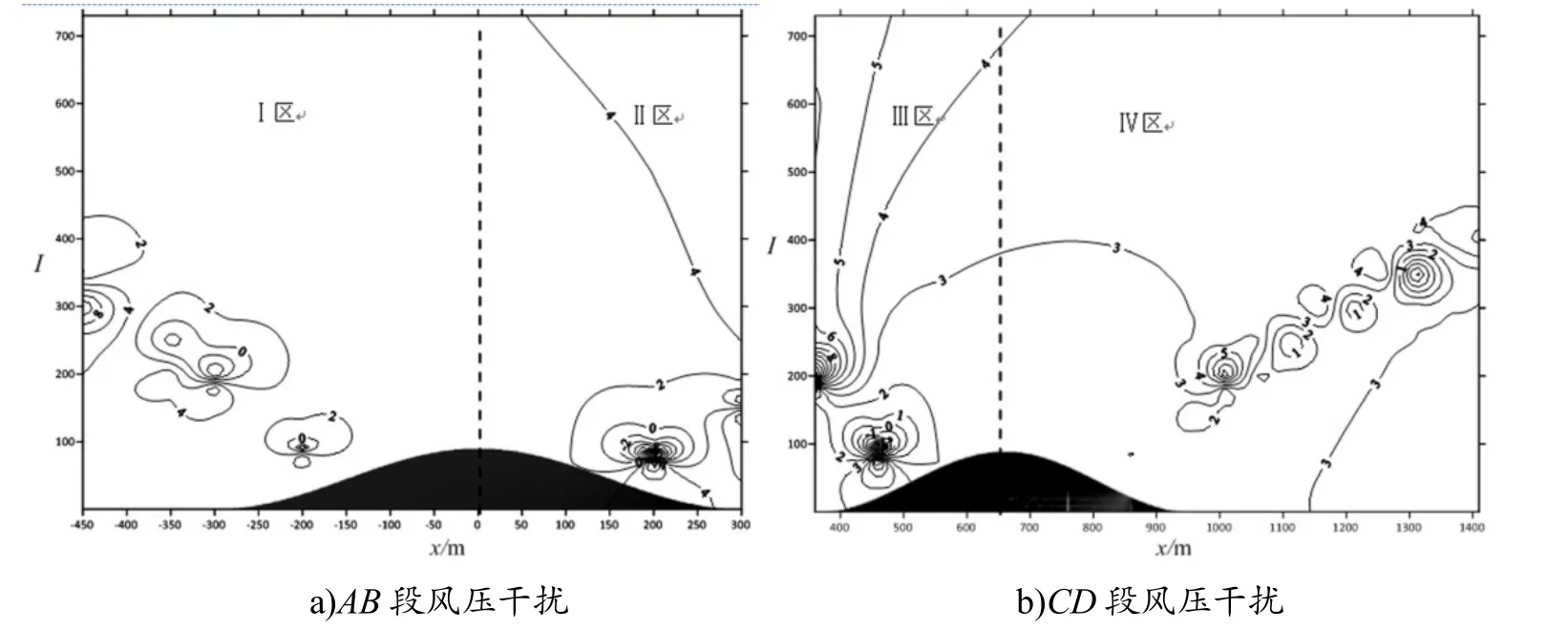
图8 间隔W=60 m 风压干扰等值线
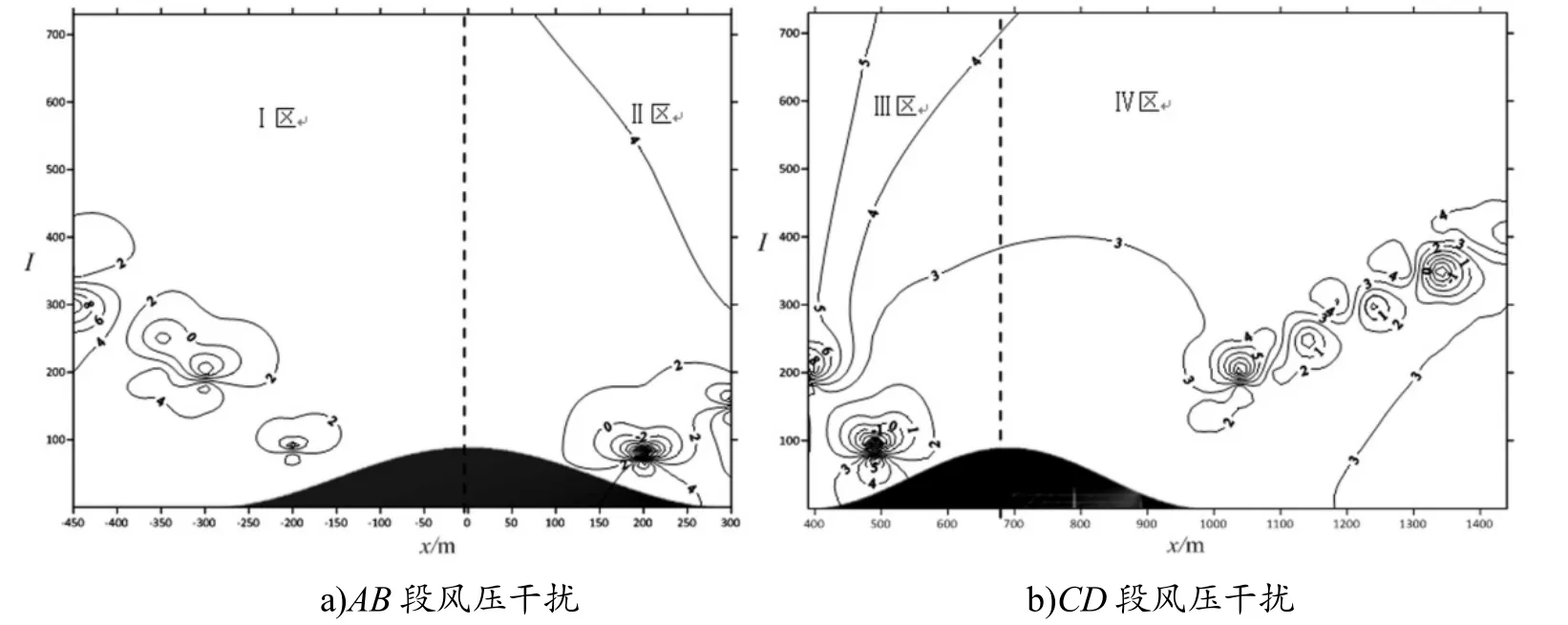
图9 间隔W=90 m 风压干扰等值线
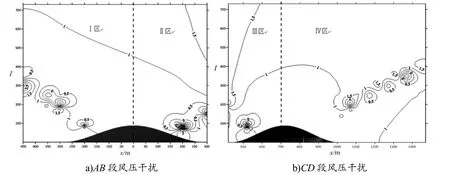
图10 间隔W=120 m 风压干扰等值线
图11 和图12 为两山间隔150 和200 m 时的风压干扰图﹒4 个区域的干扰效应和图10 大致相同,干扰因子数值较小,为0~2﹒等值线的走向与之前的工况也相同,随着两山间隔的增加,两山间互相干扰的位置都为山体斜上45°方向﹒
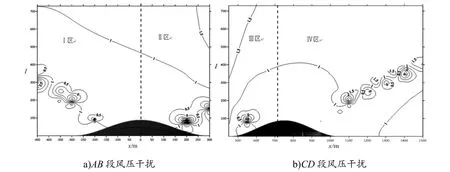
图11 间隔W=150 m 风压干扰等值线

图12 间隔W=200 m 风压干扰等值线
5 结论
1)双山间隔在W=30~90 m 时,两山之间的相互干扰作用显著,尤其是前山对后山的干扰﹒其风压系数与单山相比,最大干扰因子在后山山顶竖直向上高度200 m 处,达到8;其余区域的干扰因子在高度300 m 内取值也较大﹒由此表明,该间隔下不适合建筑物的选址﹒
2)双山间隔大于山高时,对本文而言,间隔W=120 m 及以上,其相互干扰现象不明显,可以等同两单山考虑﹒对于坡度相同高度不同的山体,此结论同样适用﹒
