2019年“八下”中考题演练

陈德前

1.（山西）下列二次根式中是最简二次根式的是（    ）.

2.（毕节）如图1，点E在正方形ABCD的边AB上.若EB=1，EC=2，那么正方形ABCD的面积为（    ）.

A.√3    B.3

C.√5    D.5

3.（常德）下列运算中正确的是（    ）.

4.（锦州）如图2，一次函数y=2x+l的图象与坐标轴分别交于A，B两点.O为坐标原点.则△AOB的面积为（    ）.

A.1/4    B.1/2

C.2    D.4

5.（淄博）如图3，矩形内有两个相邻的正方形，其面积分别为2和8.则图中阴影部分的面积为（    ）.

A.、√2    B.2

C.2√2    D.6

7.（上海）下列命题中假命题是（    ）.

A.矩形的对角线相等

B.矩形对角线交点到四个顶点的距离相等

C.矩形的对角线互相平分

D.矩形对角线交点到四条边的距离相等

8.（黄冈）已知林茂的家、体育场、文具店在同一直线上，图5中的信息反映的过程，是林茂从家跑步去体育场，在体育场锻炼了一阵后又走到文具店买笔，然后再走回家，图中x表示时间，y表示林茂离家的距离.依据图中的信息，下列说法中错误的是（    ）.

A.体育场离林茂家2.5 km

B.体育场离文具店1 km

C.林茂从体育场出发到文具店的平均速度是50 m/min

D.林茂从文具店回家时的平均速度是60 m/min

9.（雅安）如图6，在四边形ABCD中，AB=CD，AC，BD是对角线.E，F，G，H分别是AD，BD，BC，AC的中点，连接EF，粥，GH，HE.则四边形EFGH的形状是（    ）.

A.平行四边形  B.矩形

C.菱形    D.正方形

10.（荆州）如图7，矩形ABCD的顶点A，B.C分别落在∠MON的边OM，ON上，若OA =OC，要求只用无刻度的直尺作∠MON的平分线，小明的作法如下：连接AC，BD交于点E，作射线OE，则射线OE平分∠MON.有以下几条几何性质：①矩形的四个角都是直角：②矩形的对角线互相平分;③等腰三角形“三线合一”.小明的作法的依据是（    ）.

A.①②    B.①③

C.②③    D.①②③

11.（泸州）一个菱形的边长为6，面积为28.则该菱形的两条对角线的长度之和为（    ）.

A.8    B.12    C.16    D.32

12.（泰安）某射击运动员在训练中射击了10次，其成绩如图8所示，下列结论中不正确的是（    ）.

A.众数是8环

B.中位数是8环

C.平均数是8.2环

D.方差是1.2

13.（眉山）如图9，在矩形ABCD中，AB=6，BC=8.过对角线交点D作EF⊥AC，交AD于点E，交BC于点F则DE的长是（    ）.

A.1  B.7/4  C.2  D. 12/5

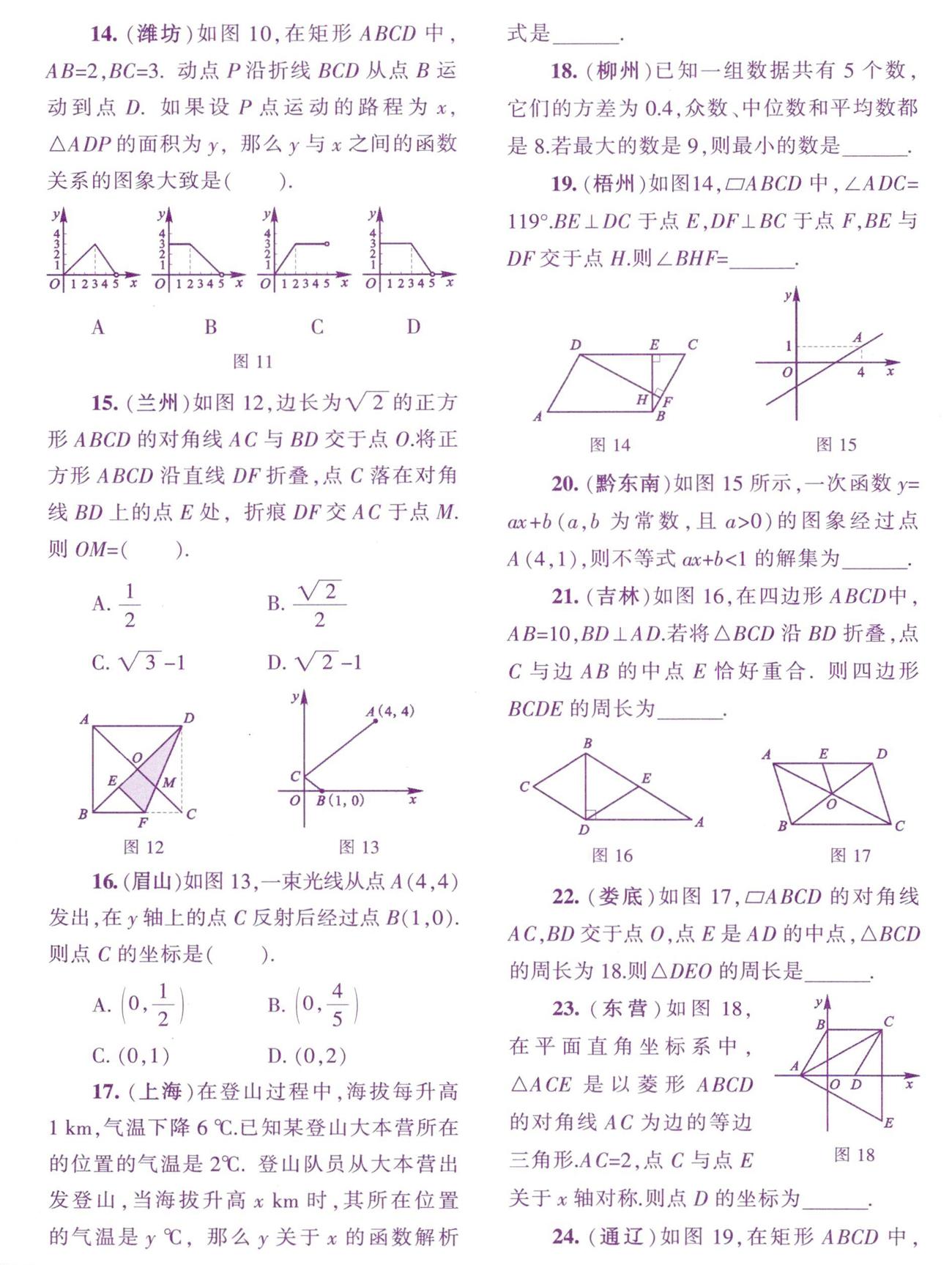
14.（潍坊）如图10，在矩形ABCD中，AB=2.BC=3.动点P沿折线BCD从点B运动到点D.如果设P点运动的路程为x，△ADP的面积为y，那么），与x之间的函数关系的图象大致是（    ）.

15.（兰州）如圖12，边长为√2的正方形ABCD的对角线AC与BD交于点D.将正方形ABCD沿直线DF折叠，点C落在对角线BD上的点E处，折痕DF交AC于点M.则OM=（    ）.

16（眉山）如图13，一束光线从点A（4，4）发出，在y轴上的点C反射后经过点B（1，0）.则点C的坐标是（    ）.

A.（0，1/2  B.（0，4/5）

C.（0，1）    D.（0，2）

17.（上海）在登山过程中，海拔每升高1 km.气温下降6℃.已知某登山大本营所在的位置的气温是2℃，登山队员从大本营出发登山，当海拔升高x km时，其所在位置的气温是y℃，那么y关于x的函数解析式是 ____.

18.（柳州）已知一组数据共有5个数，它们的方差为0.4.众数、中位数和平均数都是8.若最大的数是9，则最小的数是 ___ .

19.（梧州）如图14，◇ABCD中，∠ADC=119°.BE⊥DC于点E，DF⊥BC于点F，BE与DF交于点H.则∠BHF=____.

20.（黔东南）如图15所示，一次函数y=ax +b（口，6为常数，且a>0）的图象经过点A（4，1），则不等式ax+b<1的解集为    .

21.（吉林）如图16，在四边形ABCD中，AB=10，BD⊥AD.若将△BCD沿BD折叠，点C与边AB的中点E恰好重合.则四边形BCDE的周长为____.

22.（娄底）如图17，oABCD的对角线AC，BD交于点O.点E是AD的中点，△BCD的周长为18.则△DEO的周长是

23.（东营）如图18，在平面直角坐标系中，△ACE是以菱形ABCD的对角线AC为边的等边三角形.A C=2.点C与点E关于x轴对称，则点D的坐标为__。

24.（通辽）如图19，在矩形ABCD中，AD=8.对角线AC与BD相交于点O.AE上BD，垂足为点E，且AE平分∠BAC.则AB的长为____

25（安顺）如图20，在Rt△ABC中，∠A=90°，AB=3，AC=4.点D是斜边BC上的一个动点.过点D分别作DM⊥AB于点M，DN⊥AC于点N.连接MN.贝J线段MN的最小值为_____.

26（遵义）如图21，平行四边形纸片ABCD的边AB ，BC的长分别是10 cm和7.5 cm.将其四个角向内对折后，点B与点C重合于点C，点A与点D重合于点A.四条折痕围成一个“信封四边形”EHFG，其顶点分别在平行四边形ABCD的四条边上，则EF=____ cm.

28.（天津）如图22，正方形纸片ABCD的边长为12，E是边CD上一点.连接AE.折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上，若DE=5，则GE的长为_____

29.（兰州）如图23，A C=8.分别以A，C为圆心，以长度5为半径作弧，两条弧分别相交于点B和D.依次连接A，B，C，D，连接BD交AC于点O.

（1）判断四边形ABCD的形状并说明理由：

（2）求肋的长.

30.（云南）如图24，四边形ABCD中，对角线AC，肋相交于点O，AO=OC，BO=OD，且∠AOB=2∠OAD.

（1）求证：四边形ABCD是矩形;

（2）若∠AOB：∠ODC=4：3，求∠ADO的度数.

31（常德）某生态体验园推出了甲、乙两种消费卡，设人园次数为x时所需费用为y元，选择这两种卡消费时，y与x的函数关系如图25所示.

（1）分别求出选择这两种卡消费时，y关于x的函数的表达式;

（2）请根据入园次数确定选择哪种卡消费比较合算.

32.（聊城）如图26，在菱形ABCD中，点P是BC边上一点，连接AP.点E.F是AP上的两点，连接DE，BF，使得∠AED= ∠ABC，∠ABF=∠BPF.

（1）求证：△ABF≌△DAE;

（2）求证：DE=BF+EF.

33.（荆门）如图27，已知oABCD中，AB=5，BC=3，A C=2√13.

（1）求◇ABCD的面积;

（2）求证：BD⊥BC.

34.（甘肃）如图28所示，在正方形ABCD中，點E是BC的中点，连接DE.过点A作4G⊥DE，交加于点F，交CD于点G.

（1）试证明：△ADG≌△DCE;

（2）连接BF，证明：AB=FB.

35.（上海）在平面直角坐标系中，已知一次函数的图象平行于直线y=2x，经过点A（2，3），且与x轴交于点B.

（1）求这个一次函数的解析式;

（2）设点C在y轴上，当AC=BC时，求点C的坐标.

36.（孝感）为加快“智慧校园”建设，某市准备为试点学校采购一批A，B型号的一体机.经过市场调查发现，今年每套B型一体机的价格比每套A型一体机的价格多0.6万元，且用960万元恰好能购买500套A型一体机和200套B型一体机.

（1）今年每套A型和B型一体机的价格各是多少万元？

（2）该市明年计划采购A型和B型一体机共1100套.考虑到物价因素，预计明年每套A型一体机的价格比今年上涨25%，每套B型一体机的价格不变.若购买B型一体机的总费用不低于购买A型一体机的总费用，那么该市明年至少需要投入多少万元才能完成采购计划？

37.（大庆）如图29，在矩形ABCD中，AB=3.BC=4.M，N在对角线AC上，且AM=CN.E，F分别是AD，BC的中点.

（1）求证：△ABM≌△CDN;

（2）点G是对角线AC上一点，∠EGF90°.求AG的长.

38.（青岛）如图30，在口ABCD中，对角线AC与BD相交于点O，点E，F分别为OB.OD的中点.连接AE，OF延长AE至G，使EG=AE，连接CG.

（1）求证：△ABE≌△CDF.

（2）当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由.

39.（宁波）某风景区内的公路如图31所示，风景区内有免费的班车，班车从入口处出发，沿该公路开往草甸，途中停靠塔林（上下车时间忽略不计）.第一辆班车上午8点发车，以后每隔10 min有一辆班车从人口处发车，小聪周末到该风景区游玩，他上午7：40到达人口处.因还没到班车发车时间，于是他从风景区入口处出发，沿该公路步行25 min后到达塔林.离入口处的路程y（m）与时间x（nun）的函数关系如图32所示.

（1）求第一辆班车离人口处的路程），（m）与时间x（min）的函数关系式.

（2）求第一辆班车从入口处到达塔林所需的时间.

（3）小聪在塔林游玩40 min后，想坐班车到草甸，则小聪最早能够坐上第几辆班车？如果他坐这辆班车到草甸，比他在塔林游玩结束后立即步行到草甸提早了几分钟？（假设每辆班车速度相同，小聪步行速度不变）

40.（大庆）甲、乙两地间的直线公路长为400 km.-辆轿车和一辆货车分别沿该公路从甲、乙出发，以各自的速度匀速相向而行，货车比轿车早出发1h，途中轿车出现了故障，停下维修，货车仍继续行驶.1 h后轿车故障被排除，此时接到通知，轿车立刻掉头按原路原速返回甲地（接到通知及掉头时间不计）.最后两车同时到达甲地.两辆车距各自出发地的距离y （km）与轿车所用的时间x（h）的关系如图33所示.请结合图象解答下列问题：

（1）货车的速度是一  km/h，轿车的速度是___ km/h，t的值为____，

（2）求轿车距其出发地的距离），（km）与所用时间x （h）之间的函数关系式，并写出自变量x的取值范围：

（3）请直接写出货车出发多长时间两车相距90 km.

41.（贵阳）（1）【数学理解】如图34所示，△ABC是等腰直角三角形，过斜边AB的中点D作正方形DECF，点E，F分别在边BC，AC上.求AB，BE，AF之间的数量关系.

（2）【问题解决】如图35，在任意的Rt△ABC内，找一点D，过点D作正方形DECF，点E，F分别在边BC，AC上.如果AB=BE+AF，求∠ADB的度数.

（3）【联系拓广】如图36，在（2）的条件下，分别延长肋，FD，交AB于点M，N.求MN，AM，BN之间的数量关系.

42.（临沂）如图37.在正方形ABCD中.E是DC边上的一点（与D，C不重合），连接AE.将△ADE沿AE所在的直线折叠，

得到△A FE.延长EF交BC于G，连接AG.作GH⊥AG.与AE的延长线交于点H，连接CH.显然，AE是∠DAF的平分线，EA是∠DEF的平分线，请仔细观察，逐一找出图中其他的角平分线（仅限于小于1800角的平分线），并说明理由.

（答案在本期找）