初中数学教学中学生思维能力的激发与培养策略探究

摘 要：随着课程改革的不断深入，提高学生的各方面能力已经逐渐成为教师教学的主要任务，而数学思维能力对学生来说是非常重要的，不论是学习或日常生活都是必不可少的一种能力，是数学核心素养的重要组成部分，数学课堂教学活动是最能培养和激发数学思维的活动，教师应在教学活动中创设活动情境，激发与培养学生的数学思维能力。

关键词：初中数学;思维能力;激发;培养

一、 创设“陷阱”，促进思维的严谨性

数学是一门较为抽象的学科，学生在学习过程中对知识的理解和运用是一个渐进发展的过程，学生由于各方面原因审题不够仔细，从而导致在知识运用中出错或考虑不全面。同时学生在运用所学的知识解决问题时，也常常因为思维片面、思维定式、思维疏漏等原因导致考虑不全面。根据这些特点，在课堂教学中，教师可以结合教学内容设置一些易错题让学生练习，由于思维的片面性，考虑不全面，很多学生解题的时候会出现漏解，导致解题出错，教学中教师针对学生解题中出现的错误进行分析讲评，学生通过对错题的订正反思，促进思维的严谨性。

二、 一题多解激活思维，培养求异思维

在数学课堂上，教师可以根据教学内容采用一题多解的教学，开拓学生思维，培养数学思维的发散性。一题多解是指通过对某个数学问题采用不同的思维途径，产生不同的解决策略。在教学中创造性地使用一题多解的教学，能有效地训练学生的求异思维，开拓解题视角，利用所学的知识解决实际问题，从而培养学生数学思维的形成。因此在数学教学过程中，教师应引导学生对同一问题尝试用不同的方法解决，通过一题多解的解题训练，鼓励学生对同一问题运用不同的方法想出解决问题的策略，这样不仅可以拓宽学生的思路，让所学知识之间的联系更紧密，而且活跃了学生的思维，有助于培养求异思维。例如，在学习多边形这节内容时，可以引入下面这道例题进行一题多解的训练教学。

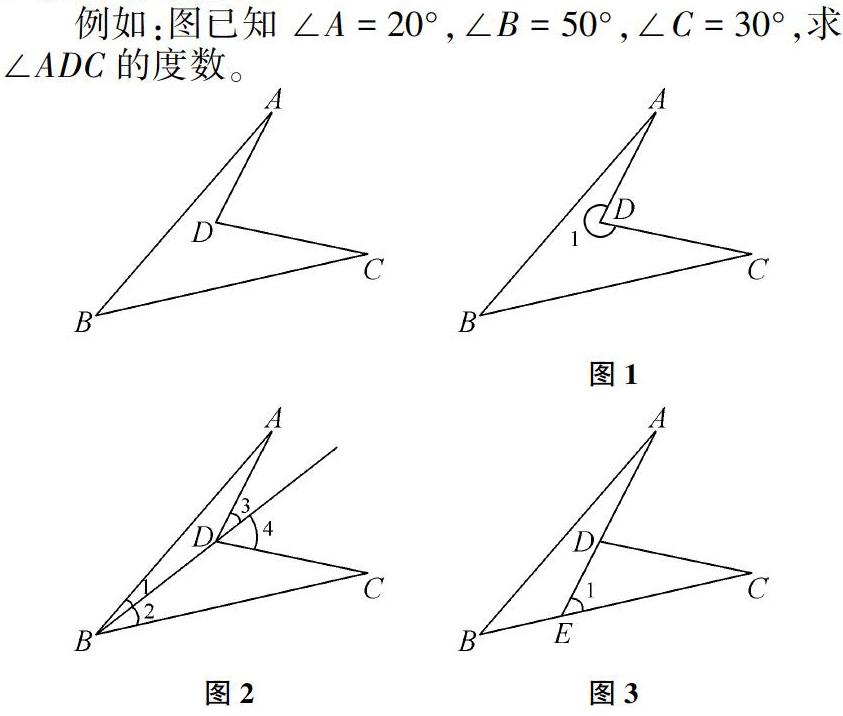
方法二：利用三角形的外角知识来解决问题。如图（2）连接BD并延长BD来解决。如图（3）连接AD并延长AD交BC于点E来解决。

方法三：利用三角形的内角和知识来解决。如图（4）连接AC

方法四：利用三角形的外角与平行线的知识来解决。如图（5）过D作EF∥BC交AB于点E可求解，具体解题过程略。

三、 拓展延伸，促进思维升华

习题是教材中的重要一部分，是提升学生对数学知识综合应用能力的关键因素，在教学中，学生通过做习题，学生的思维能力、应用实践能力，得到了激发与培养，这是课堂教学中培养学生思维能力的一个重要环节。通过习题练习并进行拓展延伸，可以很好地对学生进行思维能力的深入训练。

拓展3：如图（8）已知直线AB∥CD，请观察图形，你能推导出什么结论？

像上面在教学中通过对一道习题进行练习讲解，并进一步拓展延伸，不但能巩固所学的基础知识，更重要的是使学生初步认识了解决问题的一般方法和解题技巧，尤其是辅助线的应用，学会举一反三，能从复杂的图形中识别基础模型，灵活运用，掌握数学基本的思维方式，通过拓展延伸进行思维能力的深入训练，促进数学素养的提升。通过拓展延伸一题多变，教师将相关的题目进行整合分析，让学生在学习过程中，通过对变式题的分析，进行知识的整合，以点带面形成完整的知识体系，促进学生思维能力的升华。

在教学中对课本的习题、例题进行适当变形，一题多变，开拓学生思路，激发学生积极思维，不仅让学生加深了对基础知识的理解与掌握，而且培养学生从多角度提问题的能力和发散性思维能力。

四、 动手操作、画图实践，提高思维能力

我们都清楚动作与思维是相互联系的，数学是一门较为抽象的学科，为了让学生对这种抽象的学科有所感悟，我们可以让学生利用学具进行动手操作、画图实践，来将这种比较抽象的东西转化得更为具体形象，提高对事物的感知，使学生的数学思维能力得到一定程度的提升。例如，在学生学完平行四边形这章时，教师可以设计如下教学活动，利用学具进行活动探究。

活动1：如图已知△ABC中，AB=AC，请用尺规作图画出四边形ABDC，使得四边形ABDC为菱形，你能有几种画法呢？并说明画法的依据。

活动1在给定的等腰△ABC的基础上画菱形ABDC，换句话说给定一个菱形的三个顶点，要确定第四个顶点的问题，根据菱形的定义，一组邻边相等的平行四边形是菱形，由已知条件AB=AC可知满足一组邻边相等，只需要再满足四边形ABDC是平行四边形就行了，学生根据学过的平行四边形的判定方法，利用尺规作图就可以确定出平行四边形ABDC的第四个顶点D的位置，在活动1画菱形这一操作过程中，将平行四边形的四种判定方法的知识点串起来，通过展示不同的作法，将菱形的定义和平行四边形的四种判断方法渗透进教学中，让所有的学生都参与进行画图实践操作，激发了學生的学习积极性，又让学生充分发表自己的作图方法、观点，不断追寻不同的作法，培养了学生的求异思维。

活动2：已知△ABC中，AB=AC，你能用尺规作图画出以点A、B、C为顶点的正方形吗？若能，请说明理由，若不能，则需添加什么条件？

活动2是在活动1的基础上进行提升，通过这样的变式，训练学生的探究欲望在不知不觉中被激起，数学思维能力也跟着被激发起来。通过画图可以知道，要画出正方形ABDC，在活动1画出菱形ABDC的基础上，只需添加一个角为直角，也就是说，只需△ABC应为等腰直角三角形，即添加∠BAC=90°。我们都知道思维开始于动作，在教学中让学生通过实践动手操作画图，进而直观感知，可以有效地培养学生的直观想象素养，促进思维的内化。数学是一门具有抽象性的学科，在教学中通过让学生动手实践，可以提高学生对事物的感性认识，促进数学思维能力进一步激发。

五、 逆向思考，促进创造性思维的发展

在教学中，我们要培养学生的多种思维方式，避免因固定思维方式而影响了学生的思维创新发展，在教学中多对学生进行逆向思考训练，就能打破惯性思维定式，培养逆向思维，促进创造性思维的发展。在教学中，教师可以精心设计教学方式，增加逆向应用的练习，不断培养学生的逆向思维，增强学生的创造性思维能力。

总之，数学思维能力对于一个初中生来说是一项十分重要的能力，通过课堂教学培养学生的思维能力与思维品质，是新课程改革背景下教师肩负的一项重要任务。教师在数学课堂教学中有目的、有计划地进行易错题训练、一题多解训练、拓展延伸训练、动手操作画图实践、逆向思考训练，将有利于开拓学生的解题思路，激发和培养学生的数学思维，因此，教师应在平时的课堂教学活动中精心创设问题情境，使学生有足够地动脑的时间、思考的空间，逐步培养学生良好的思维能力与数学素养，促进学生综合素质的全面发展。

参考文献：

[1]陈海烽.利用实验探究 提高复习效率[J].中学数学教学参考，2018（3）：4.

[2]罗永亮.把握三种语言[J].中学生数理化：七年级数学（人教版），2010（11）：1.

[3]司孟秋.小学生思维能力的培养[J].学周刊，2013（16）：68-69.

作者简介：蔡丽碧，福建省厦门市，厦门市翔安第一中学。