数学学习中助推学生深度思考

摘 要：深度学习是学生主动参与，积极思考，大胆探索，勇于质疑的学习过程，其本质特征是深度思考。小学数学学习的深度思考主要表现在学生对数学概念的理解与应用，能正确运用所学的数学知识和方法进行判断、推理，去分析和解决问题，培养思维品质。

关键词：理解;质疑;辨析;深度思考

学生在数学课堂上深度学习的基本特征是深度思考。它是针对学生在知识建构和问题解决过程中，思考问题的肤浅、片面，应用知识的生搬硬套，回答问题的支离破碎等而提出来的。小学数学学习的深度思考主要表现在学生对数学概念的理解与应用，学生思考问题的思维品质。因此，在小学生数学学习过程中教师要着重关注学生对数学概念的意义理解，运用所学的数学知识和方法进行判断、推理，去分析和解决问题，培养学生的思维品质。

一、 意义理解掌握概念

深度学习是学生对数学概念、性质、法则自主意义理解的学习，而不是死记硬背、生搬硬套的学习。我会背了不等于我理解了;我会做题了也不等于我理解了。对于数学概念的意义理解源于学生的自主建构，教师的任务就是要创设问题情境对接学生的已有知识和经验，为学生提供丰富的感性材料引导学生自主去探索，帮助学生将所学的新知识纳入原有的认知结构中，形成知识体系。例如：在《认识平行四边形》教学中，学生对平行四边形已经有了初步的感知，本节课的重点就是要让学生理解掌握平行四边形的特征，进一步丰富头脑中平行四边形的空间表象。教学中我用课件出示各种方位大小不一样的平行四边形，提出问题：这些图形的大小、方位各不相同为什么都叫平行四边形呢？它们有什么共同特征呢？请同学们先观察猜测，再应用老师在学具袋里为大家准备的学具（方格纸、小棒和若干个剪好的平行四边形）验证自己的猜测。组织汇报时：

生1：我选择两组相等的小棒，每组2根，拼成了一个，我发现平行四边形的两组对边分别相等。

生2：我借助方格纸上画一个平行四边形，在画的过程中我发现平行四边形的两组对边分别相等，而且互相平行。

生3：我选择几个平行四边形量它们的边长，我发现平行四边形的两组对边分别相等。

生4：我也选择几个平行四边形用三角尺推一推，我发现平行四边形的两组对边分别平行。

……

刚才同学们通过观察猜测验证，发现了平行四边形的这些特征，那谁能说一说什么样的图形叫做平行四边形？

生1：两组对边分别平行的四边形叫做平行四边形。

生2：两组对边分别相等的四边形叫做平行四边形。

生3：两组对边分别平行而且相等的四边形叫做平行四边形。

在学生基本理解平行四边形概念的基础上，教师出示一个平行四边形框架，拉动框架演示，当拉成邻边夹角是直角时，学生说是长方形，也有的学生说还是平行四边形。此时引导学生思考：长方形有什么特征？它具备平行四边形的所有特征吗？引导学生展开对话交流，让学生应用概念进行说理，在交流中进一步理解平行四边形的概念。在此基础上理解正方形是特殊的长方形，长方形是特殊的平行四边形也就不难了。如果让你把正方形、长方形、平行四边形分别填入下面图形中，请填一填并说明理由。

学生在说理的过程中进一步理解了平行四边形的概念，理解平行四边形、长方形、正方形三者之间的关系。

二、 应用知识深化理解

深度学习的意义在于学生理解掌握了数学知识的基础上，能够应用所学的知识进行分析、判断、推理，能够应用所学的知识解决新问题或解决真实情境中的数学问题。引导深度学习就是要精心设计问题串，让学生卷入学习，应用概念进行思考、说理，培养学生的思辨能力。例如：在教学三角形三边关系时，学生通过自主探索发现：三角形的任意两边之和一定大于第三边。这个规律是动态变化的，两条短边之和大于最长边，到一定范围后最长边就变成了较短边。这对四年级的学生理解起来有一定的困难，必须在练习中去自主感悟。因此，我设计了如下的练习：（1）下面三组线段首尾相接能围成三角形的是（  ）;

A. 4厘米、8厘米和12厘米，

B. 5厘米、8厘米和11厘米，

C. 7厘米、7厘米和15厘米;（2）一个三角形中，如果两条较短的边长分别是6厘米和10厘米，那么第三条边长（取整厘米数）可能是（  ）厘米;（3）一個三角形中，如果一边长5厘米，另一边长12厘米，那么第三边（取整厘米数）最长是（  ）厘米，最短是（  ）厘米。这三道题由浅入深，学生应用“三角形中任意两边之和大于第三边”这个知识点进行思考，在判断、推理中加深对知识的理解。

三、 反思质疑深入理解

“学贵有疑”。疑是学之始，思之有所得。在探索知识和运用知识解决问题的过程中，时常要求学生停下脚步，反思自己的学习心路历程，反思在探索过程中遇到的困难与障碍，反思克服困难的过程与方法，反思在探究过程中所产生的困惑。要让学生充满好奇心和求知欲，要鼓励学大胆质疑，不唯书，不唯师，在质疑中探索，在探索中求证，不断将学生的学习思考引向深入。例如：苏教版六年级上册《认识百分数》例1教学时，学生理解了李明投篮25次，投中16次，投中的比率是64%;张小华投篮20次，投中13次，投中的比率是65%;吴力军投篮30次，投中18次，投中的比率是60%;得出百分数便于比较，张小华投中的比率高一些。结果有个学生质疑：老师，我觉得这样比较不公平，如果我投篮1次，投中了，投中的比率是100%，这样是不是我的投中比率更高些呢？我们知道虽然百分数便于比较，那是针对大数据而言的，而对于极值是不宜参与比较的，因此我觉得苏教版教材在这里是否存在一点瑕疵呢？又如：在教学平均数时，老师设计一道题：小华身高155厘米，一条河流的某一段平均水深40厘米，小华想从这里过河有危险吗？学生通过对话交流基本达成共识：平均水深40厘米，说明有的地方比40厘米深，有的地方比40厘米浅，小华过河有危险，学生基本理解了平均数的内涵;可是有个小男孩却坚持说没有危险，因为平均水深40厘米，就一定有比40厘米浅的地方，小华只要选择比40厘米浅的地方过河就没有危险。原来他是个农村孩子，经常蹚水过河积累了一定的生活经验，河床宽的地方往往比较浅。虽然这种质疑属于个别现象，但学生能质疑、敢质疑，说明学生对百分数、平均数的概念有了比较深入的理解，同时也提醒老师们设计练习既要考虑考查的目的性，编题的合理性、科学性，还要注意严谨性。

四、 辨析论证深刻理解

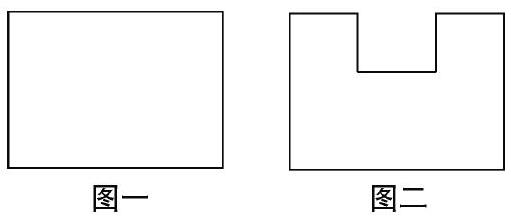
深度学习就是在学习中能全面、系统、深入地思考问题，它往往在自我对话、同伴争辩中经历思维的碰撞把思考推向深入走向深刻。一个话题、一个知识点经过不断辨析论证思路会更清晰，理解更深刻。在数学概念学习中，教师要精心策划，善于把握辩论素材，引导学生展开辩论。例如：在认识面积的教学中，教师让学生通过摸一摸、比一比等各种感知活动，初步理解“物体表面或平面图形的大小叫做它的面积”的概念后，设计一道练习让学生深化理解面积概念。下面这两个图形的面积，哪个面积大？

有的学生说图一的面积大（甲方），有的同学认为是图二的面积大（乙方），意见不统一。我就组织甲乙双方展开辩论。

甲方：因为图二有个缺口，所以图一比图二面积大。

乙方：虽然图二有个缺口，但把底下那条线往上移就能补平，还多出两条线，所以图二面积比图一大。

甲方：面积比的是围成图形的大小，指的是里面部分，而不是比边线的长短。

乙方：图二总是比图一多两条线段啊。

甲方：那只能说明图一的周长比图二短。

……

甲方还是不能完全说服乙方。此时，请同学们拿出彩笔描出图一和图二的周长，比一比哪个图形的周长长，再涂一涂两个图形的面积，并比一比。在描涂的过程中，乙方同学终于认同了甲方的观点，对面积和周长都有了进一步深刻的理解，明确面积和周长是两个不同的概念，并且感悟到周长大的图形面积不一定就大。

总之，深度学习是学生主动参与，积极思考，大胆探索，勇于质疑的学习过程，在自主探索的基础上，全面理解数学概念的本质，把握概念的内涵和外延，并灵活应用概念进行分析、思考、判断、推理，使自己的认识更加深刻。

参考文献：

[1]谢毅，马刚.“平行四边形的认识”课堂教学实录与评析[J].山东教育，2007.

[2]陈贵.自制教具在初中几何教学中的应用：以“四边形”教学为例[J].北京教育学院学报（自然科学版），2015.

作者简介：谢盛强，福建省宁德市，福建省霞浦县实验小学。