可见-短近红外成像光谱数据的土壤有机质含量估算

焦彩霞，郑光辉*，解宪丽，崔雪峰，赏 刚

1. 南京信息工程大学地理科学学院，江苏 南京 2100442. 中国科学院南京土壤研究所，江苏 南京 2100083. 北京师范大学系统科学学院，北京 100875

引 言

土壤有机质(soil organic matter,SOM)是土壤的重要组分，是植物营养物质的来源，它在形成土壤团聚体、提高土壤含水量、减少土壤退化和侵蚀方面具有重要作用[1]。土壤反射光谱技术成功实现了快速、低成本SOM估算[2-4]，特别是近年建立的全球土壤反射光谱数据库更有助于满足区域至全球范围土壤评价与监测的需求[5]。土壤反射光谱技术仅提供样点数据，无法提供面状数据以表现土壤水平方向及剖面垂直方向的连续变异。遥感技术是实现土壤有机质快速制图的重要方法[6-7]，但目前的遥感数据用于土壤有机质制图尚存在混合像元、水分、光谱分辨率等影响因素，因此提取土壤成像光谱数据的有效信息、建立土壤有机质光谱指数，是应用现有遥感数据进行SOM制图及研制未来SOM制图专用传感器的理论前提。彭杰[8]研究结果表明，570～630 nm波段为SOM敏感波段，600 nm反射率与SOM相关系数最大。Zheng等[9]与徐彬彬和戴昌达[10]分析土壤有机质反射光谱数据的吸收特征波段、建立600 nm“弓曲差”光谱指数，成功实现了土壤有机质含量估算。因此，本工作利用风干、研磨后土壤样品的成像光谱数据，建立600 nm“弓曲差”(deviation of arch,DOA)光谱指数并构建SOM估算模型，与偏最小二乘回归(partial least square regression，PLSR)结果相比较，探讨该光谱指数用于SOM制图的可行性，为未来SOM遥感制图奠定理论与方法基础。

1 实验部分

1.1 土壤样本采集与属性测定

研究区位于江苏省东台市，该区域东临黄海，属北亚热带暖湿季风气候区。区内土壤以公元1028年完工的范公堤为界，堤西地区为湖相沉积形成的水稻土，堤东为近千年黄河、长江沉积物经人类耕作发育形成的潮盐土。样品分为两批采集(图1)： 2013年采集8个表土(0～5 cm)及20个剖面土样，每个剖面内分别采集0～5，5～10，10～20，20～30，30～40，40～60，60～80和80～100 cm共8个深度的土壤样品； 2018年采集11个剖面土样，每个剖面内分别采集0～5，5～10，10～15，15～20，20～30，30～40，40～50，50～60，60～80和80～100 cm共10个深度的土壤样品。共采集土壤样品278个。样品自然风干后研磨过100目筛，分成两份分别用于成像光谱及土壤属性测定。土壤有机质由重铬酸钾氧化-外加热法测定。

1.2 成像光谱数据采集与预处理

土壤样品装于铝盒盖内并用直尺刮平，放置于移动平台之上，在暗室内采集样品成像光谱数据，经黑白校正得到反射率光谱数据(图2)。仪器为加拿大Lumenera公司生产的INFINITY V10E成像光谱仪，在389～1 045 nm光谱范围采集256个波段的数据，人工光源为4盏卤素灯。采集得到的成像光谱反射率数据在ENVI 5.3软件中通过ROI提取每个土壤样品的平均反射光谱曲线，去除两端误差较大波段、保留425～1 015 nm共230个波段数据用于后续计算与分析。

图1 采样点位置分布图Fig.1 Location of samples

图2 成像光谱数据采集及预处理过程图Fig.2 Collection and preprocessing of imaging spectroscopy

1.3 建模方法

使用非线性参数回归及偏最小二乘回归两种方法。非线性参数回归以光谱数据计算出的光谱指数600 nm“弓曲差”为自变量，可称为DOAR(DOA Regression)； 600 nm“弓曲差”是指每一条土壤光谱曲线的600 nm反射率与其550和650 nm光谱反射率平均值的差[10]。偏最小二乘回归以230个波段的光谱数据为自变量。偏最小二乘回归集典型相关分析、主成分分析与多元线性回归分析于一体，可以较好解决自变量多重共线性问题，允许在样本个数少于变量个数条件下进行回归建模。这种方法广泛应用于反射光谱估算土壤属性的研究[11-12]。

(1)

(2)

(3)

1.4 样本集划分及建模预测

模型精度会随样本集划分结果而变化[14]。为避免样本集划分对模型结果的影响、更好地分析模型的稳定性，对样本集进行1 000次随机抽样，每次取1/2样本作为建模样本集，剩余1/2为预测验证集，进行1 000次建模与预测验证，并计算每次的RMSE、R2和RPD用于统计分析。

2 结果与讨论

2.1 土壤有机质含量统计分析

由表1可知，研究区内土壤有机质含量较低(平均值为8.72 k·kg-1)，变异较大(最小值为1.39 k·kg-1，最大值为52.56 k·kg-1，变异系数为87.65%)。堤东潮盐土为近千年形成，成土年龄较短，有机质含量显著低于堤西水稻土，平均值分别为7.43和15.92 k·kg-1。

2.2 “弓曲差”非线性回归结果分析

土壤有机质含量与“弓曲差”的相关系数为-0.68，表明有机质含量增加会使“弓曲差”减小； 反之逐步减小的“弓曲差”表示样本中有机质含量的逐渐增加。这种负相关关系是“弓曲差”估算土壤有机质含量的机理。由散点图(图3)可见，对数函数可以比线性函数更好地拟合土壤有机质含量与“弓曲差”的函数关系，调整R2为0.524 2。徐彬彬和戴昌达[10]的研究结果与本研究相同，但Zheng等[9]研究表明线性函数拟合结果最优。通过对比可以发现，样本有机质含量变化范围对土壤有机质含量与“弓曲差”的关系影响最大，即有机质含量变化范围大会导致两者呈对数关系，有机质含量变化范围小时两者呈线性关系。

表1 土壤有机质含量描述统计Table 1 Descriptive statistics of SOM content

图3 土壤有机质与“弓曲差”散点分布图Fig.3 Scatter plot of SOM and DOA

使用对数函数分别建立1 000次随机划分建模集的预测模型并使用预测集独立样本进行模型验证，1 000次的建模及验证结果统计见表2。建模R2变化范围为0.28～0.69，平均值为0.52； 预测验证R2变化范围为0.02～0.64，平均值为0.49，RPD平均值为1.42。预测验证R2总体小于建模R2且最小值为0.02，表明在一些数据集划分的情况下会产生比

表2 DOA回归结果统计表Table 2 Statistics of DOA regression

较差的预测结果，但大部分预测及建模R2大于0.45(图4)，说明由成像光谱数据计算的光谱指数“弓曲差”可以较好地预测样品有机质含量。

图4 建模及预测验证决定R2频率统计图

2.3 偏最小二乘回归结果分析

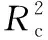
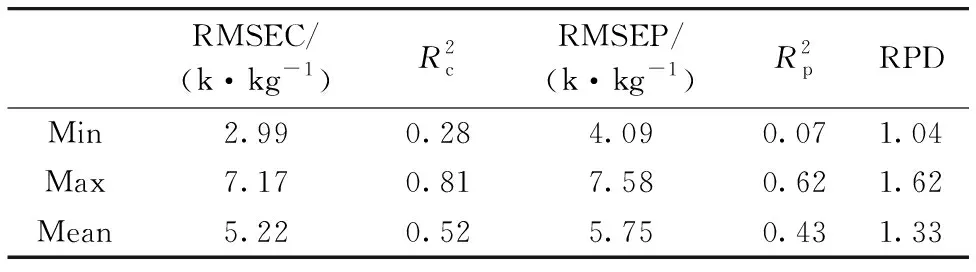
表3 偏最小二乘回归结果统计表Table 3 Statistics of partial least square regression

3 结 论

通过1 000次随机抽样方法划分建模与预测验证数据集、利用“弓曲差”非线性回归及偏最小二乘回归两种方法建立土壤有机质估算模型，通过精度对比探讨“弓曲差”方法估算SOM的有效性与稳定性。研究发现，有机质含量与600 nm“弓曲差”呈负相关关系，是该光谱指数应用于SOM估算的机理。虽然DOAR仅提取了三个波段的光谱信息，但其建模精度与PLSR方法相当，预测验证精度优于PLSR。可以得出结论，DOA方法可以用于室内土壤成像光谱数据的SOM制图。此研究为高分五号及珠海一号等卫星遥感数据应用于SOM研究提供了新的思路。