随机优化算法应用于太赫兹测厚方法的研究

张洪桢，何明霞*，石粒力，王鹏騛

1. 天津大学精密测试技术及仪器国家重点实验室，天津 3000722. 天津大学精密仪器与光电子工程学院，天津 3000723. 南京大学电子科学与工程学院超导电子学研究所，江苏 南京 210023

引 言

太赫兹检测技术是重要的前沿交叉领域，太赫兹波对于大多数非极性物质透明，能够分析物质在太赫兹频段的频谱特征或对其进行成像[1]，在材料性质和结构的无损检测领域具有广阔的应用前景，如检测不同种类纸张的厚度与介电常数[2]、分析文物、油画等艺术品的结构和内部缺陷[3-4]、测量药片的覆膜厚度[5]与孔隙率[6]等。随着工业4.0的时代的到来，对先进制造提出了更高的要求，在生产线上实现在线、非接触的无损高精度检测是必然趋势。

截至目前，已经进行了许多关于太赫兹波应用于涂层厚度测量的研究[7]。Su[8]等测量了金属和非金属(碳纤维)基底上油漆涂层的厚度，其测量值与超声波测厚结果保持了良好的一致性。Izutani[9]等测量了多层样品的太赫兹波形，并计算了波形中各脉冲回波的飞行时间。Yasui[10]、林玉华[11]等利用最小二乘法对油漆样品的光学厚度与几何厚度之间的关系进行建模，得到不同油漆的折射率，测量了最多三层油漆样品的厚度，并绘制了厚度的三维分布图。Nguyen[12]等通过采取不同入射角度，控制太赫兹波在样品中的光程，实现了对较薄涂层样品的测量工作，但是该方法要求样品具有较为平坦的表面，不能对具有明显曲率的涂层样品进行测量。

1 原 理

1.1 基于太赫兹频谱的厚度测量模型

太赫兹波(Terahertz wave)对大多数非极性材料呈现接近透明特征，当太赫兹脉冲入射到不同材料介质中时，由于各介质群折射率的不连续性，脉冲在介质界面处发生反射，形成了具有不同飞行时间的反射脉冲，如图1所示。

图1 太赫兹时域光谱测量油漆厚度原理图(a): 油漆涂层模型； (b): 太赫兹脉冲回波的飞行时间Fig.1 Principle of thickness determination by THz-TDS(a): Model of coatings； (b): Times of flight of THz echoes

根据太赫兹在多层介质中的传播理论，可得单层样品的太赫兹回波信号

(1)

与双层样品的太赫兹回波信号

(2)

Erefi为第i个反射信号,Δti为第i个回波信号与入射信号Ein之间的飞行时间差。定义拟合误差为

(3)

Emea为实测太赫兹脉冲回波信号。根据菲涅尔定律，在正入射条件下(i=2,3)

(4)

(5)

(6)

可得Etotal中系数k1和k2

k1=r12

(7)

k2=t12r23t21

配合画展的《谭建丞山水册页精品集》收录了谭老山水画册页126件，是1968年到1972年期间所创作，由思澂斋出版。■

(8)

对于单层样品，依据式(4)和式(7)即可反解出深层折射率n2; 对于双层样品，需依据式(4)—式(8)对第一层深层的折射率n2和第二层深层的折射率n3进行求解。

根据飞行时间原理，可得材料厚度计算模型

(9)

ΔTi=Δti-Δti-1

(10)

其中c为真空中的光速，ni为第i层材料的折射率。

1.2 随机最优化算法

与确定性寻优算法相比，随机优化方法提供了诸多便利。该类算法基于随机性、统计性和概率性，增大了得到全局最优值的概率，可应用于不可微、非连续、非线性、含噪声和具有多维变量的目标函数。相比于以梯度为核心的优化算法，随机优化算法具有较强的收敛性，能够有效收敛至最优解。本文采用差分进化算法(DE)求解回波信号Etotal中ki和Δti等参数，通过一定次数的迭代寻优，获得使fittederror达到最小的最优解ki,best和Δti,best，进而求解被测样品各层厚度di。

2 实验部分

实验采用Menlo System Tera K15全光纤式太赫兹时域光谱系统，由飞秒激光器、发射天线、接收天线、光纤延迟线以及锁相装置组成，中心波长为1 560 nm，太赫兹频谱宽度达到3.5 THz，激光重复频率为100 MHz，脉冲宽度<90 fs，平均功率>100 mW。本实验以铝合金板材作为基底，使用保赐利品牌的自动喷漆制作了单层、双层油漆涂层等多种样品,基底尺寸7 cm×7 cm。在同一块基底上规划样品和参考区域，在测量时，通过步进电机改变样品架位置实现对样品信号与参考信号的测量。利用涡流测厚仪SIN-EC770在样品区域连续测量十组数据，计算测量结果的均值并将其作为太赫兹测厚方法的参考。

3 结果与讨论

3.1 单层油漆厚度及折射率测量结果

使用涡流涂层测厚仪SIN-EC770对浸锌漆、黑色漆以及底漆等三种单层样品的厚度进行十次测量，测量结果的均值如表1。

利用第1部分中提出的方法拟合脉冲回波的总信号Etotal。由于浸锌漆厚度较厚>200 μm，反射信号Eref1与Eref2在时域能够明显区分，飞行时间差ΔT=Δt2-Δt1=5.92 ps，反射系数k1=r12=0.597 5。根据式(4)，式(7)和式(9)可求得样品厚度d=223.71 μm。为了验证差分进化算法运算结果的稳定性，针对每一种样品，任意选择该样品的一个太赫兹测量信号重复进行200次求解，得到200组结果并计算这些结果的不确定度。如表2所示，三种样品厚度结果的不确定度均小于0.5 μm，折射率结果的不确定度均小于0.1，且不确定度的大小与测量样品的厚度没有直接关系，说明差分进化算法的收敛性较强，运算的结果较为稳定。

表1 SIN-EC770单层油漆测量结果Table 1 Results of single coating samples by SIN-EC770

表2 DE算法计算结果Table 2 Results of single coating samples by DE algorithm

本文的方法可以准确求解厚度不小于60 μm涂层样品太赫兹信号中混叠的各个反射脉冲，如图2(a)所示，黑色漆样品的飞行时间差ΔT=0.755 2 ps。图2(b)为底漆样品的太赫兹信号，各个反射信号在时域能够明显区分，ΔT=3.360 0 ps。

图2 单层样品的测量信号与拟合结果(a): 黑色漆样品; (b): 底漆样品Fig.2 The measurement and simulation resultsof single coating samples(a): Black coating sample; (b): Base coating sample

3.2 测量误差分析

由1.1节提出的测量模型可知，当样品基底所在平面的法线方向相对于太赫兹波出射方向存在的偏移角度θ时，将会给测量的厚度带来误差。

图3 反射信号的光程误差Fig.3 Optical path error of the reflection pulse

根据图3，当样品相对平面存在小偏移角度θ时，Eref2的光程误差Δd为

(11)

参考信号的光程误差对测量结果没有影响，所以Eref2的光程误差Δd为测量误差的主要来源，由于sin2θ趋近于0，进而Δd近于0，由小偏移角度带来的光程误差可以忽略不记，表3示出了三种样品在多个偏移角度下的测量误差。

表3 测量误差(偏移角θ=1°)Table 3 Measurement errors (angle offset θ=1°)

当偏移角度过大时，太赫兹探头无法全部接收由分束器反射回来的太赫兹波，导致接收的信号能量发生损失，根据式(6)和式(7)将无法准确计算样品的折射率，此时，需要借助其他手段对样品的折射率进行标定。

3.3 双层油漆测量结果分析

在测量银漆+底漆双层油漆样品厚度时，先喷涂底漆，之后再喷涂银漆，待样品干燥之后测量总厚度，SIN-EC770的测量结果为121.6 μm。在喷涂银漆时，底漆未完全干燥，二者在交界面处发生混合，形成了一层折射率介于二者之间的介质，太赫兹波将在该层“衍生介质”的两个分界面发生反射，反射回来的总信号将包含来自四个反射界面的反射脉冲，使用式(2)提出的双层模型将无法准确计算各涂层的折射率以及太赫兹波在其中的飞行时间； 如表4所示，借助式(2)模型测得的总厚度为106.5 μm，与SIN-EC770的测量结果相差较大，底漆折射率为3.56，与表2结果相矛盾。

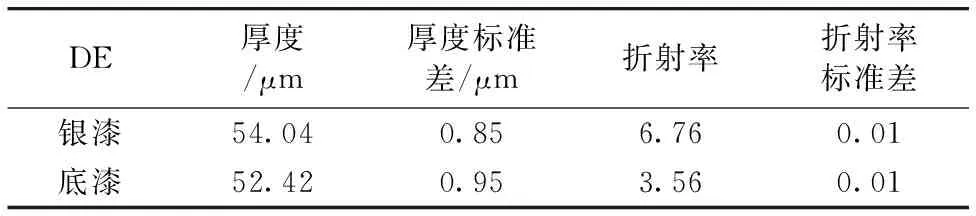
表4 底漆+银漆太赫兹方法测量结果Table 4 Results of the double coating sampleby terahertz method

该样品实际包含三层涂层，如图4所示，除了基本的反射脉冲Eref1，Eref2与Eref3外，实测太赫兹信号还包含由基底反射回来的信号Eref4与各层介质中的多重反射信号EM，由于银漆的折射率大于中间介质层，由银漆-中间介质界面反射回来的Eref2的符号为负。

图4 底漆+银漆样品反射信号与拟合信号Fig.4 Reflection and simulation signals ofthe base and silver coating sample

图5为该样品的太赫兹波光路图，各个反射脉冲的光程与其在时域上的位置具有对应关系，当样品状态发生改变时，多重反射脉冲EM和目标反射脉冲信号Eref1—Eref4在时域上的相对位置将会发生改变，EM可能会出现在Eref1与Eref4之间，在对样品中太赫兹波的光程没有先验认知的情况下，虽然可以计算各个反射信号之间的飞行时间差，但算法无法从时域信号上判断各个反射脉冲具体来自哪一个反射界面，从而无法实现对各层涂层厚度的求解。

图5 太赫兹波在多层样品中的光路图Fig.5 Paths of terahertz waves of a multi-layer sample

4 结 论

基于太赫兹时域光谱系统，根据菲涅尔定律与太赫兹脉冲的飞行时间原理建立数学模型，借助差分进化算法对模型参数进行求解，实现了对油漆厚度的自动非接触式无损测量。为了验证差分进化算法运算结果的稳定性，针对每一种样品，任意选择该样品的一个太赫兹测量信号重复进行200次求解，得到200组结果并计算这些结果的不确定度。三种样品厚度及折射率计算结果的不确定度均较小，说明差分进化算法具有较强的收敛性。对于单层样品，太赫兹测量方法表现良好，对样品基底所在平面法线方向与太赫兹波出射方向之间的角度误差具有较强的稳健性，较小的角度误差对测量结果影响可以忽略不记，测量结果与涡流测厚仪的结果相一致。在将基于飞行时间原理的测量模型拓展到多层样品的测量中时，发现太赫兹波在各层介质中的光程将影响各个反射脉冲在时域光谱上的相对位置，由于多重反射效应的存在，算法无法区分各个反射峰来自哪一个反射界面，给各层厚度的求解带来困难。

相比于涡流测厚、磁性测厚等厚度测量手段，太赫兹技术具有非接触式、无损检测等明显优势； 在满足测量精度要求的情况下，本文提出的模型实现了对厚度小于60 μm的油漆涂层的测量工作，降低了基于飞行时间原理的太赫兹测厚方法的测量极限，有效扩大了该方法的测量范围。