TDLAS技术中不同背景气体的混合气体浓度算法

陈 昊，鞠 昱，韩 立，常 洋

1. 中国科学院电工研究所，北京 1001902. 中国科学院大学，北京 1000493. 北京航天易联科发展有限公司，北京 100176

引 言

可调谐半导体激光光谱技术(tunable diode laser absorption spectroscopy，TDLAS)是近年来发展十分迅速的光谱检测技术，它利用激光能量被气体分子“选频”吸收形成吸收光谱的原理来测量气体浓度，具有高灵敏度、响应速度快、安全性能高、检测极限达到ppb量级等优点，被广泛地应用于工业检测、安全防护、气象监测等领域[1-3]。

TDLAS直接吸收光谱法中的浓度算法主要是根据测算待测气体“选频”吸收引起的洛伦兹吸收程度来表征气体浓度[4-5]。目前常用的方法是峰值算法，它是将实测吸收谱线的线性部分拟合出基线，利用实测谱线与基线相减或相除得到的吸收谱线峰值与标准浓度进行二次拟合，得到气体浓度与峰值的对应关系，从而计算浓度[6]。但此算法对同浓度的不同背景气体的运算结果存在较大误差，原因是不同背景气体下分子碰撞程度不同，洛伦兹吸收谱线的峰值和线宽发生相应的变化，测量导致浓度失准，存在误差[7-8]。另一种常用的气体浓度的算法是积分算法，它考虑到了光谱展宽的影响，利用对洛伦兹谱线的积分来得到吸收面积，再进行二次拟合。积分算法比峰值算法误差更小，但激光器扫描波长范围有限，无法对所有洛伦兹吸收的波长范围进行积分，因此也存在误差。

通过分析TDLAS检测中同浓度不同背景气体直接吸收光谱法的洛伦兹谱线吸收程度不同的原因，提出了采用Levenberg-Marquardt算法拟合出洛伦兹吸收谱线，对面积系数和标准浓度进行二次拟合，以此表征浓度的算法，并比较了峰值、积分以及面积系数三种表征浓度算法的误差。

1 理论分析

TDLAS技术是基于Beer-Lambert定律，它描述了待测气体分子对特定波长激光进行“选频”吸收后的前后光强变化，其函数关系如式(1)

It=I0exp[-α(ν)cL]

(1)

式(1)中，It为穿过待测气体后的透射光光强，I0为入射光强，α(ν)为吸收系数，该系数与气体的种类以及穿过该气体的光频率有关，c为待测气体的浓度，L为光所经过的待测气体的吸收路径长度。

吸收系数的表达式为

α(ν)=NSg(ν)

(2)

式(2)中，N为气体分子总量，S为气体吸收谱线强度，g(ν)是归一化的吸收线型函数。在一个大气压以上的环境中，压力展宽占主导作用，采用Lorentz线型函数来描述吸收谱线。

(3)

式(3)中，ν是扫描频率，ν0是吸收谱线的中心频率，r是吸收谱线的半高宽。根据Hitran数据库的r的表达式为

(4)

式(4)中，Tref为参考温度(296 K)，T为当前气体温度，rbc为背景气体半高宽，rself为待测气体半高宽，p为总气压，pself为待测气体分压。

根据式(4)可知，环境温度、背景气体半高宽、待测气体半高宽以及两者分压比共同决定了混合气体吸收谱线的半高宽，待测气体的分压比等同于待测气体浓度，因此同浓度不同背景气体下，待测气体分压比不变，背景气体半高宽的不同导致了混合气吸收谱线的半高宽变化，引起吸收系数的改变，是洛伦兹谱线吸收程度不同的主要原因。

峰值算法和积分算法是TDLAS技术中用来表征气体浓度的两种常用方法，但它们都存在一些问题。图1是同浓度不同半高宽下直接吸收曲线和洛伦兹吸收谱的模拟结果，随着半高宽的增加，吸收峰逐渐变宽，洛伦兹吸收谱峰值变小，峰值算法存在明显误差。此外，图1(a)中直接吸收曲线的基线(虚线表示)发生偏移，而两种算法都需要对基线进行扣除，因此基线的变化会引起浓度计算出现偏差。由于激光器扫描电流覆盖的波数有限，如图1(b)所示扫描波数范围为7 297～7 303 cm-1，采用积分算法时没有计算到扫描范围外以及基线下方的区域，导致测量失准。为了克服上述问题，基于Levenberg-Marquardt算法，推导出含有基线的洛伦兹吸收谱的目标函数，对实测直接吸收谱进行非线性拟合，以目标函数中的面积系数与标准浓度二次拟合，以此表征浓度。

2 Levenberg-Marquardt算法

Levenberg-Marquardt算法是一种迭代算法，寻求多元函数与测量真值之间的最佳函数参量，是解决非线性最小二乘法问题的技术方案。通过建立目标函数，采用Levenberg-Marquardt迭代算法来拟合出洛伦兹吸收谱[9-10]。

图1 同浓度不同半高宽下吸收谱线的模拟结果

Levenberg-Marquardt算法通过反复迭代使得目标函数值与实测数值的平方值最小化，寻求最佳的待定参数解，如式(5)

f=min‖F(x)-y‖2

(5)

通过表达式(6)完成迭代计算

xj+1=xj-(H+μI)-1JTf

(6)

式(6)中，j为迭代次数，J为x的雅克比矩阵，H=JTJ为Hessian矩阵，μ为阻尼因子，(H+μI)-1JTf为迭代步长，f为ε2的最小值。

根据前面的理论分析，可知吸收谱线的一般表达式

(7)

当激光器PI曲线处在线性区域时，I0为一次线性函数，表达式中的其他部分表示了洛伦兹吸收，因此设定目标函数如式(8)

(8)

迭代计算可以通过Matlab实现，进一步得到式(8)的最优化待定系数。根据洛伦兹吸收谱线的线型定义，x1为谱线中心频率，是洛伦兹吸收谱线中心峰值的频率位置；x2为谱线半高宽系数，表征了洛伦兹吸收谱线展宽程度；x3为面积系数，表征了整体的洛伦兹吸收程度；x4ν+x5是基线函数。将最优化待定系数带入目标函数，扣除基线函数，获得拟合后的洛伦兹吸收谱，利用面积系数与标准浓度二次拟合，得到表征浓度的算法。整体算法流程图如图2所示。

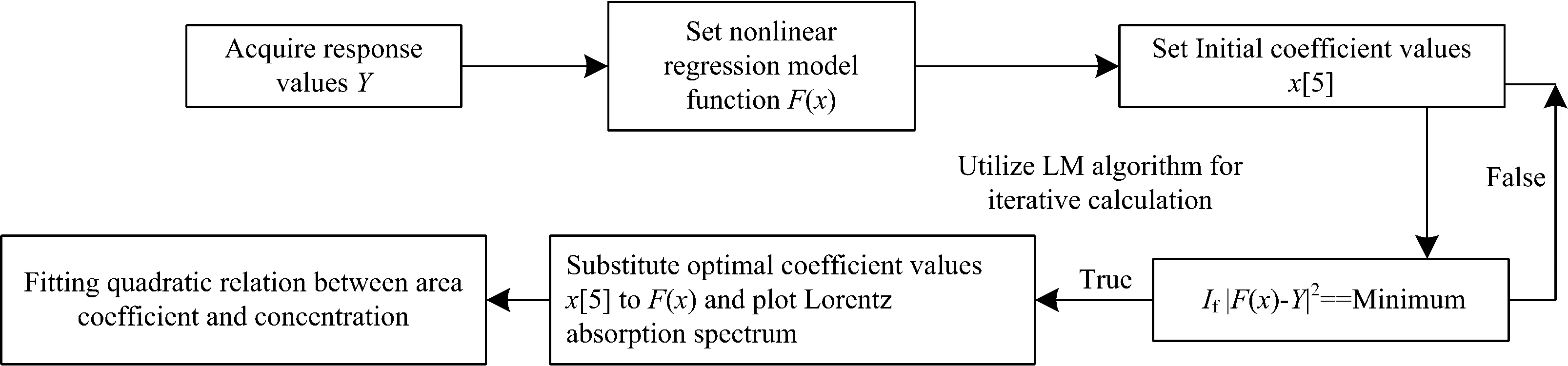
图2 基于Levenberg-Marquardt算法拟合算法流程图Fig.2 Flow chart of fitting method based on Levenberg-Marquardt algorithm

3 实验部分

实验系统由TDLAS水汽测试系统、Michell-s8000露点仪和国瑞智GRZ5013湿度发生器组成。国瑞智湿度发生器采用双压法原理，用于产生各种背景气体的相对湿度环境，Michell露点仪用来测量实际的水汽浓度。TDLAS水汽测试系统选用中心波长为1 368.59 nm的DFB半导体激光器，气室长度30 cm，通过单片机产生低频的锯齿波电流信号，激光器经过电流调制后，输出光信号波长覆盖水汽吸收峰，光信号在气室中进行反射吸收进入探测器，最终由上位机对信号进行处理。

图3 测试系统整体结构图Fig.3 Test system overall structure diagram

根据Hitran数据库，实验选取了1 368.579 nm波长的水汽吸收峰，吸收强度为1.8×10-20cm-1·(molec·cm-2)-1，背景气体选取了浓度为99.99%的氩气、99.99%的氮气和干燥空气，通过国瑞智湿度发生器产生40%～80%的相对湿度环境，湿度间隔10%，温度为25℃，Michell露点仪水汽测量结果作为参考，将TDLAS水汽测试系统的气室探头放入湿度发生器环境箱中，PC端读取每个测试环境的直接吸收曲线，利用Levenberg-Marquardt算法拟合出洛伦兹吸收谱线，对三种算法进行了误差分析。测试系统整体结构如图3所示。

4 结果与讨论

4.1 拟合洛伦兹吸收谱线

通过拟合处理后得到三种背景气体下不同浓度水汽的直接吸收曲线和洛伦兹吸收谱，图4(a)，(b)和(c)是干燥空气、氮气和氩气的直接吸收曲线，(d)，(e)和(f)是对应的背景气体下拟合后的洛伦兹吸收谱。从结果上看同浓度下氩气为背景气体的洛伦兹吸收谱的峰值明显高于氮气和干燥空气的谱线峰值，谱线的半高宽比氮气和干燥空气的谱线半高宽要窄，氮气和干燥空气的洛伦兹吸收谱的峰值和半高宽比较接近。为了获得更为准确的结论，需要对结果进行定量分析。

图4 三种背景气体的直接吸收曲线和洛伦兹吸收谱Fig.4 Direct absorption spectra and Lorentz spectra of three background gases

4.2 三种算法误差的定量分析

首先通过计算干燥空气为背景气体下的洛伦兹吸收谱的峰值、积分以及面积系数，以每个相对湿度测试点的Michell露点仪水汽浓度测量值为参考，得到三种算法的二次拟合关系，再利用得到的三种算法的拟合关系来计算氮气、氩气背景下的浓度值，并与Michell露点仪的实测进行对比，误差分析。

4.2.1 氮气背景下三种浓度算法的对比结果

表1是氮气下峰值、积分以及面积系数算法的浓度对比结果，从图6的相对误差分析结果上看，峰值算法的最大相对误差为-11.64%，最小相对误差为-7.79%,相对误差均方值为0.88%； 积分算法的最大相对误差为2.65%，最小相对误差为-0.56%，相对误差均方值为0.03%； 面积系数算法的最大相对误差为1.76%，最小相对误差-0.54%，相对误差均方值为0.01%。实验表明峰值算法误差较大，积分和面积系数算法误差接近，面积系数算法略优于积分算法。

表1 氮气下峰值、积分以及面积系数算法的浓度对比结果Table 1 H2O Concentration in three algorithms under background gas of N2

4.2.2 氩气背景下三种浓度算法的对比结果

表2是氩气下峰值、积分以及面积系数算法的浓度对比结果，从图7的相对误差分析结果上看，峰值算法的最大相对误差为109.27%，最小相对误差为73.04%，相对误差均方值为87.57%； 积分算法的最大相对误差为-10.13%，最小相对误差为-5.51%，相对误差均方值为0.61%； 面积系数算法的最大相对误差为2.96%，最小相对误差为1.34%，相对误差均方值为0.06%。实验表明峰值算法浓度结果严重失准，面积系数算法的误差最小，优于另外两种算法。

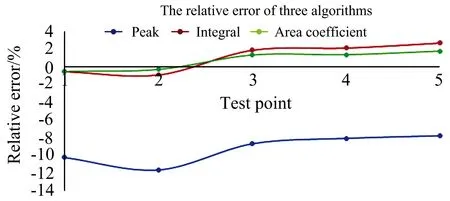
图5 氮气下峰值、积分以及面积算法的浓度相对误差

实验中的干燥空气是利用空气压缩机直接抽取室内空气进行除湿后的气体，含有78.09%的氮气，与99.99%的氮气相比，两者成分比较接近，分子质量基本相同，而在标准大气压下，分子间的碰撞展宽占主导因素，是洛伦兹吸收变化的主要成因，因此两者谱线线型比较相近，氮气下三种算法浓度相对误差均方值也比较接近(最大不超过0.88%)，面积系数算法的误差最小。而同浓度下氩气为背景气体的洛伦兹吸收谱线峰值要明显高于空气和氮气，半高宽变窄，因此峰值算法的相对误差急剧增加，此时面积系数的相对误差均方值最小(0.06%)，优于峰值(87.57%)和积分(0.61%)的相对误差均方值，说明了本文提出的面积系数算法误差最小，测量结果更为接近实测值。

图6 氩气下峰值、积分以及面积算法的浓度相对误差

表2 氩气下峰值、积分以及面积系数算法的浓度对比结果Table 2 H2O Concentration in three algorithms under background gas of Ar

5 结 论

基于可调谐半导体激光光谱技术(TDLAS)对干燥空气、氮气和氩气为背景气体的水汽洛伦兹吸收谱线型展宽机理进行了分析，提出了采用Levenberg-Marquardt算法拟合出洛伦兹吸收谱，利用面积系数表征浓度的算法，以Michell露点仪的水汽测量值作为参考，对比了峰值、积分和面积系数算法下的水汽浓度相对误差。实验表明： 氮气下峰值、积分和面积系数算法的最大相对误差为-11.64%，2.65%和1.76%，相对误差均方值分别是0.88%，0.03%和0.01%； 氩气下峰值、积分和面积系数算法的最大相对误差为-109.27%，-10.13%和2.96%，相对误差均方值分别是87.51%，0.61%和0.06%； 面积系数表征浓度算法最优，误差最小，结果最为准确。