应用有限元方法分析步进梁式加热炉的水梁固定梁

王 波

(中钢集团洛阳耐火材料研究院有限公司，河南 洛阳 471039)

1 有限元方法简介

在许多实际工程问题中，一般不能得到精确解，这要归因于微分方程组的复杂性，以及难以确定的边界条件和初值条件。为了解决这个问题，要借助数值方法来求近似解。有限元方法是一种数值解法。有限元方法使用积分方法而不是微分方法来建立系统的代数方程组。而且该方法用一个连续的函数来近似描述每一个单元的解。由于内部单元的边界是连续的，整个问题的解就可以通过单个的解连接或组装起来。应力分析之中的稳态、瞬态、线性或非线性问题以及热传导、流体流动和电磁学中的问题都可以用有限元方法进行分析。本文讨论步进炉梁式加热炉的水梁固定梁的稳态，线性的应力分布和极值等[1]。

2 采用有限元分析的优势

目前很多设计企业都存在着“傻、大、粗”的现象，即在没有精确的计算手段的前提下，为了充分保证结构的安全，参考以前的经验使用过大型号的型材、管材等。虽然解决了安全隐患，但是却过多地浪费了资源。随着社会的发展，这些非可再生资源越来越珍贵，材料的合理利用也更加重要了。我们需要更加精确的分析计算手段。如果可以通过计算、分析使我们准确地找到合适的型材，并得出结构的薄弱之处，加以强化，这样不仅节省资源，也大幅降低了产品的成本。而且有限元方法可以对结构进行整体的分析，使结果更接近真实的情况。

有限元分析方法可以满足计算精度要求。使用有限元方法可以解决带有复杂几何条件和复杂边界条件的问题。

3 对加热炉水梁固定梁进行有限元分析。

以某钢厂120 t/h步进梁式加热炉为例，进行水梁固定梁的分析，料坯截面150 mm×150 mm，坯长6～12 m，步距30 cm，固定梁分两段。

3.1 建立模型

首先建立固定梁1∶1模型，如图1所示。

图1 水梁固定梁1∶1模型

3.2 施加边界条件和荷载

施加装、出料端料坯的不同的荷载及重力场等(见图2)。

图2 施加边界条件和荷载

3.3 得出分析结果

3.3.1 挠度

分析图3、图4，可看到固定梁及立柱的变形趋势，最大挠度为0.31 mm。

图3 固定梁挠度云图

图4 局部放大云图

3.3.2 应力云图(常用的von Mises应力)

图5～图7为固定梁应力分析图。可见，应力最大值为15.68 MPa，产生在第二和第五根梁上，关于炉子中心线对称。

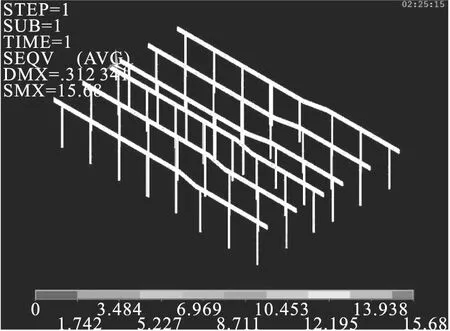
图5 固定梁应力云图

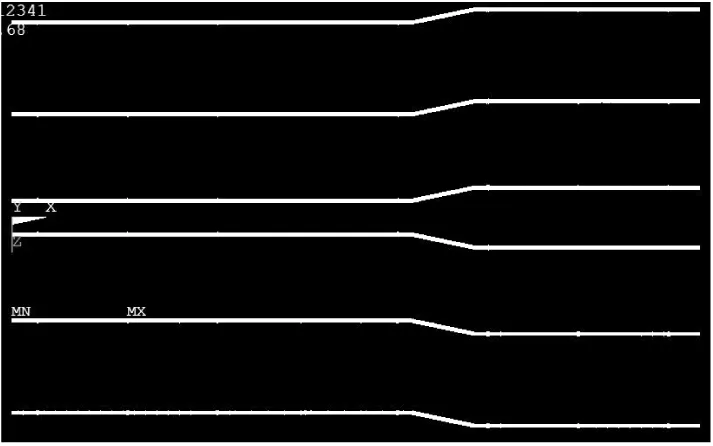
图6 固定梁应力极值点

图7 局部放大云图

3.3.3 应变云图

图8为固定梁应变云图。

图8 固定梁应变云图

分析图8可以得到应变为0.007 6%。

3.3.4 支反力及弯矩

表1为本例中54个支点的反力及弯矩(支点为立柱下端点)。支反力为炉底钢结构提供计算数据，本文不做炉底钢结构分析的讨论。

从表1中不仅可以得到每一个支点的反力及弯矩，也可以结合云图选择显示某一点的数据，或者事先制定好与设计相关的重要的点，直接输出，由于篇幅有限，此处不再列出。

3.3.5 结构变形数据

可以得到每一个点的变形数据，也可以结合云图选择显示某一点的数据，或者事先制定好与设计相关的重要的点，直接输出。图9为选取点的截图。

表2为本例节点(共1 086个)的变形数据(只选取一部分)，数据可以生成表格、曲线、动画等。

表1 54个支点的反力及弯矩

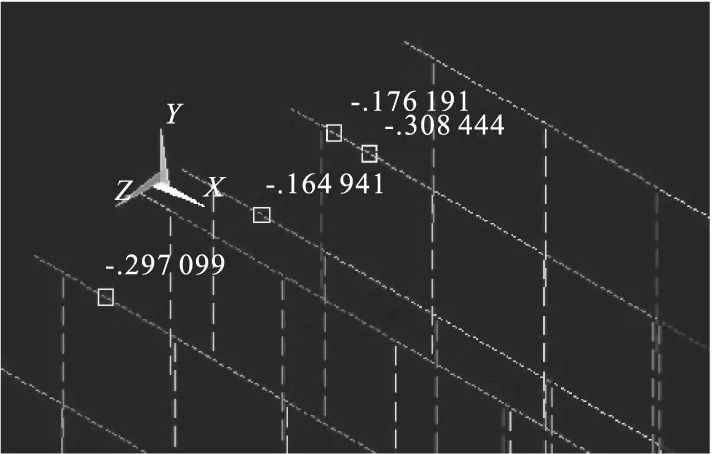
图9 梁的变形数据选取点图

4 结 论

根据以上分析的结果，可以得出：

(1)采用有限元分析方法计算工程结构是可行的。

(2)有限元方法可以分析结构的多项参数，简化计算。

(3)有限元方法可以对结构整体进行分析，提高计算精度。

表2 部分节点变形数据

(4)根据计算结果，可以针对性的优化结构。

(5)采用有限元方法得到的分析结果更为精确、直观、灵活。可以用云图，图表，曲线，动画等多种方式来表示。