多工序加工单元的移动机器人调度优化

2020-11-06顾斌斌明全华张翼飞

造船技术 2020年5期

顾斌斌，明全华，张翼飞

(1.沪东中华造船(集团)有限公司，上海200129；2.中国船级社质量认证公司上海分公司，上海200135)

0 引言

在多工序加工单元中，实现物流搬运的方式多种多样，其中移动机器人以其高自动化、高柔性等优点得到广泛应用。目前，国内外学者对机器人调度问题做了许多研究。沈博闻等[1]研究基于机器人的自动化仓储模式，建立一个灵活可重构的仓储空间模型，制订适用于仓储物流的机器人运行规则，分解物流任务，给出机器人调度方法，修正其算法实现在特殊道路约束下的路径规划，进而加入时序建立时间空间地图进行三维路径规划。雷卫东等[2]研究一类带时间窗口的自动化混流生产线的工件排序和机器人作业排序问题；基于对研究问题的分析，考虑处理时间窗口约束、机器人搬运能力约束和工作站能力约束，使用混合整数规划方法建立此类问题的通用数学模型，并通过自动化印刷电路板生产线实例和大量随机生成算例验证所建模型。DANG等[3]研究单机器人的上料顺序问题，提出一种基于遗传算法的启发式算法，并应用叶轮生产线验证方法的有效性。

由上述文献可以看出：先进的调度算法是解决机器人调度问题的关键。对于采用单轨多机器人调度的多工序加工单元，不同工序的加工时间、设备数量及上下料点与不同设备间物理位置的差异，使得各设备间加工任务的合理配置存在较大意义。以某企业动力电池生产线容量确定单元为例，以最小化调度时间为目标，建立多移动机器人调度优化模型，并设计遗传算法求解得出合理的分配方案，提高调度效率。

1 问题描述

在一个多移动机器人多工序动力电池生产单元内，共有同类型的i个产品需依次经过j道工序完成加工。各工序加工时间不一、设备数量不一，并按工序顺序沿机器人轨道依次排开。单元由1个上料口、1个下料口、2个机器人及设备和缓冲区构成。工件由上料口Din进入，由机器人Rk负责在各工序间流转，最终由下料口Dout移除单元。单轨多移动机器人调度模型如图1所示，其中Baj表示工件a的缓冲区编号Bj,Mai表示工件a的目标设备Mi。

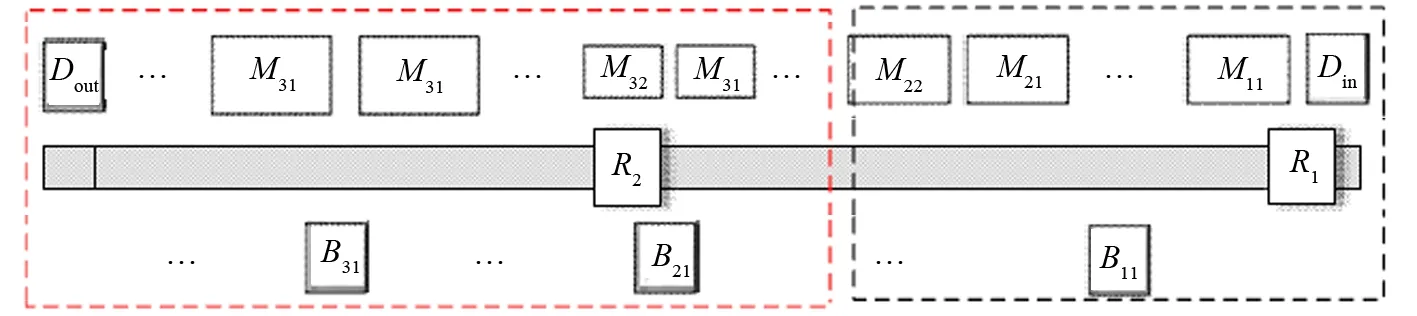
图1 单轨多移动机器人调度模型

从实际生产情况出发，对研究问题做如下假设：(1)机器人行驶速度一定，且各台移动机器人速度一致；(2)机器人单次只能响应1个任务，1次只能抓取1个产品；(3)机器人服务设备时停靠点确定，即各设备、上下料点、缓冲区间的运输距离已定；(4)机器人抓取料件后若下一工序存在空闲设备且在服务范围内，则移动机器人直接放料至该设备，否则放料至相应缓冲区；(5)机器人在完成任务后可直接响应下一任务并前往相应位置；(6)每道工序有且仅有一个缓冲区；(7)缓冲区由传送带构成，且缓冲区容量不影响移动机器人调度；(8)移动机器人在取料后直接响应缓冲区上料任务。

2 数学模型

为便于问题描述，现将一些基本符号进行说明，如表1所示。

表1 模型相关符号及其意义

约束模型构建如下：

βMi≤A,∀Mi

(1)

式(1)表示单元内设备可并行处理多个工件，式中：βMi为设备Mi的可加工数量；A为设备最多能够并行处理的工件数量。

TbaMi≥Tbkas+T(Ikks,Mi)

+T(Mi,Ma),∀M,a,s

(2)

式(2)表示设备需在机器人完成上料任务后开始充放电，式中：TbaMi为工件a在设备Mi上加工开始的时间节点；Tbkas为机器人开始执行工件a搬运任务s的时间节点；T(Ikks,Mi)为机器人从开始执行搬运任务s时其所在的设备Ikks移动到Mi所用时间；T(Mi,Ma)为机器人从设备Mi移动到Ma所用时间。

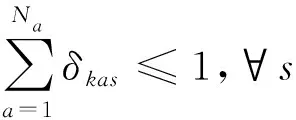
(3)

式(3)表示机器人单次只能抓取1个工件，式中：δkas为机器人Rk执行工件a搬运任务s的过程。

KRk0=M1Rk

(4)

式(4)表示机器人起始位置在其服务范围的首个设备位置，式中：KRk0为机器人Rk的起始位置；M1Rk为机器人Rk服务范围内的首个设备位置。

Tbkas+Tkas≥TeaMi,∀M,a,s

(5)

式(5)表示机器人需在设备加工完成后开始执行取料任务，式中：Tkas为机器人执行搬运任务s时，装载工件a前设备所用时间；TeaMi为工件a在设备Mi上加工完成的时间节点。

Tekas-Tbkas=δkasTks,∀a,s

(6)

式(6)表示搬运任务结束时间是开始搬运工件i的时间加上搬运时间，式中：Tekas为机器人完成工件a搬运任务s的时间节点；Tks为机器人执行搬运任务s所用时间。

TeaMi=TbaMi+Taj,∀a,M

(7)

式(7)表示工件完工时间等于开始时间加上加工时间，式中：Taj为工件a在工序j上的加工时间。

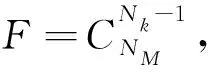
(8)

根据上述约束模型，目标函数为

(9)

当机器人有上料任务时，若存在目标设备剩余加工容量不为0，则完成一次搬运任务所需时间是机器人从当前位置移至上料缓冲区取料的时间加上从上料区移至目标设备的时间，如式(10)所示：

δkasTks=T(Ikks,Baj)+T(Baj,Ma),

∀a,s,∂as=1,βMa>0

(10)

式中：T(Ikks,Baj)为机器人从开始执行搬运任务s时其所在的设备Ikks移动到工件a的缓冲区Bj所用时间；T(Baj,Ma)为机器人从工件a缓冲区Bj移动到工件a的目标设备Ma所用时间；βMa为设备Ma的可加工数量；

若存在目标设备剩余加工容量等于0，设备放弃上料任务，等待完成下一下料任务后执行该上料任务。

当机器人有下料任务时，若存在目标设备剩余加工容量不为0，则完成一次搬运任务所需时间是从当前位置移至目标设备的时间加上从目标设备移至下料设备的时间，如式(11)所示：

δkasTks=T(Ikks,Iaks)+T(Iaks,Ma),∀a,k,s且∂as=0

(11)

式中：Iaks为机器人开始执行任务s时工件a所在的设备；T(Ikks,Iaks)为机器人从开始执行任务s时其所在的设备Ikks移动到Iaks所用时间；T(Iaks,Ma)为机器人从Iaks移动到工件a的目标设备Ma所用时间。

若不存在目标设备剩余加工容量不为0，或下工序设备不在该机器人服务范围内，则机器人完成一次搬运任务所需时间是从当前位置移至目标设备的时间加上从目标设备移至缓冲区位置的时间，如式(12)所示：

δkasTks=T(Ikks,Iaks)+T(Iaks,Baj),∀a,k,s且∂as=0

(12)

式中：T(Iaks,Baj)为机器人从开始执行搬运任务s时工件a所在的设备Iaks移动到工件a的缓冲区Bj所用时间。

3 算法设计

3.1 编码

分别对2台机器人编码，并将工件编号出现的次数作为机器人将该工件运至某工序对应设备的判断依据，即若在该机器人服务范围存在2道工序，每个工件编号需在个体中重复出现3次。当工件编号第1次出现时表示工件从上料区运至工序1设备，第2次出现时为从工序1设备运至工序2设备，第 3次出现时为从工序2设备运至缓冲区。同理，在机器人Ⅱ的编码中，工件编号第1次出现时表示工件从缓冲区运至工序3设备，直到下料完成加工，具体表示如图2所示。最终，通过记录机器人依次在染色体中出现时所对应的设备，解码得出机器人运输路径。

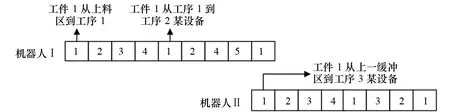
图2 机器人编码示例

3.2 选择策略

考虑到所设计的算法在初代种群生成过程中存在一定随机性，若采用传统的轮盘赌方法进行算子选择，则：在进化前期，目标函数值高的个体被选中概率过高，导致子代继承过多，子代个体单一，从而使搜索陷入局部搜索；在进化后期，个体目标函数值差距较小，无法做到有效选择[4-6]。因此，在进行轮盘赌之前，将个体的目标函数值由小到大排序，获得个体排序序号l，按式(13)计算个体的适应度值f(i)：

f(i)=a(1-a)l-1，a∈(0,1)

(13)

按式(14)计算个体的c(i)，作为其进行轮盘赌时被选中的概率上限：

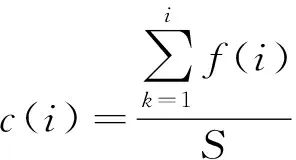
(14)

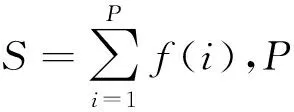
采取此方法，个体被选中的概率只取决于其在种群中的排序l与参数值a的大小，该个体与其他个体目标函数值的绝对差值大小并不会影响其遗传到子代的数量，从而在一定程度上避免了上述问题。

3.3 交叉算子

任意选取同一机器人个体a1、a2对应位置上的工件编号i1、i2：若i1=i2，不做交叉运算；若i1≠i2，将i1与i2相互交换，从a1中随机选出一个工件编号i2改为i1，并对a2展开与a1相同的修正。具体修正过程如图3所示。

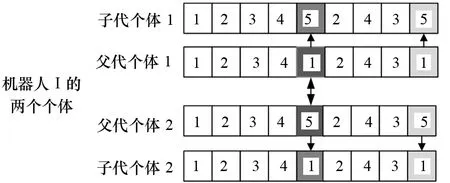
图3 交叉算子修正方法

3.4 变异算子

在算法中对于每个个体，随机生成2个[1,2Na]之间不等的整数，取这2个数位上的基因片段相互交换，产生邻域范围解，如图4所示。通过多次搜索，计算每次交换前后个体的目标函数值，选出值最小的个体作为局部搜索后的最优个体。

图4 变异算子

3.5 算法流程

(1) 设置相关参数：种群大小P，最大迭代次数D，交叉概率Pc，变异概率Pm，机器人服务范围约束矩阵R，工序约束矩阵G，初始工件节拍Rt，机器人在各节点间行驶时间表H。

(2) 机器人任务分配方案取k=1，迭代次数d=1，令分配方案总数kT=矩阵R的行数。

(3) 令J=R(k,:)，根据J中约束关系，结合工序约束顺序生成初始种群。

(4) 计算个体目标函数值。

(5) 计算个体适应度值c(i)，并执行选择操作。

(6) 交叉操作：以概率Pc对随机选取的两个个体进行交叉。

(7) 变异操作：以概率Pm对个体进行变异操作。

(8) 选出父代和子代中适应度值最高的个体作为最优个体。

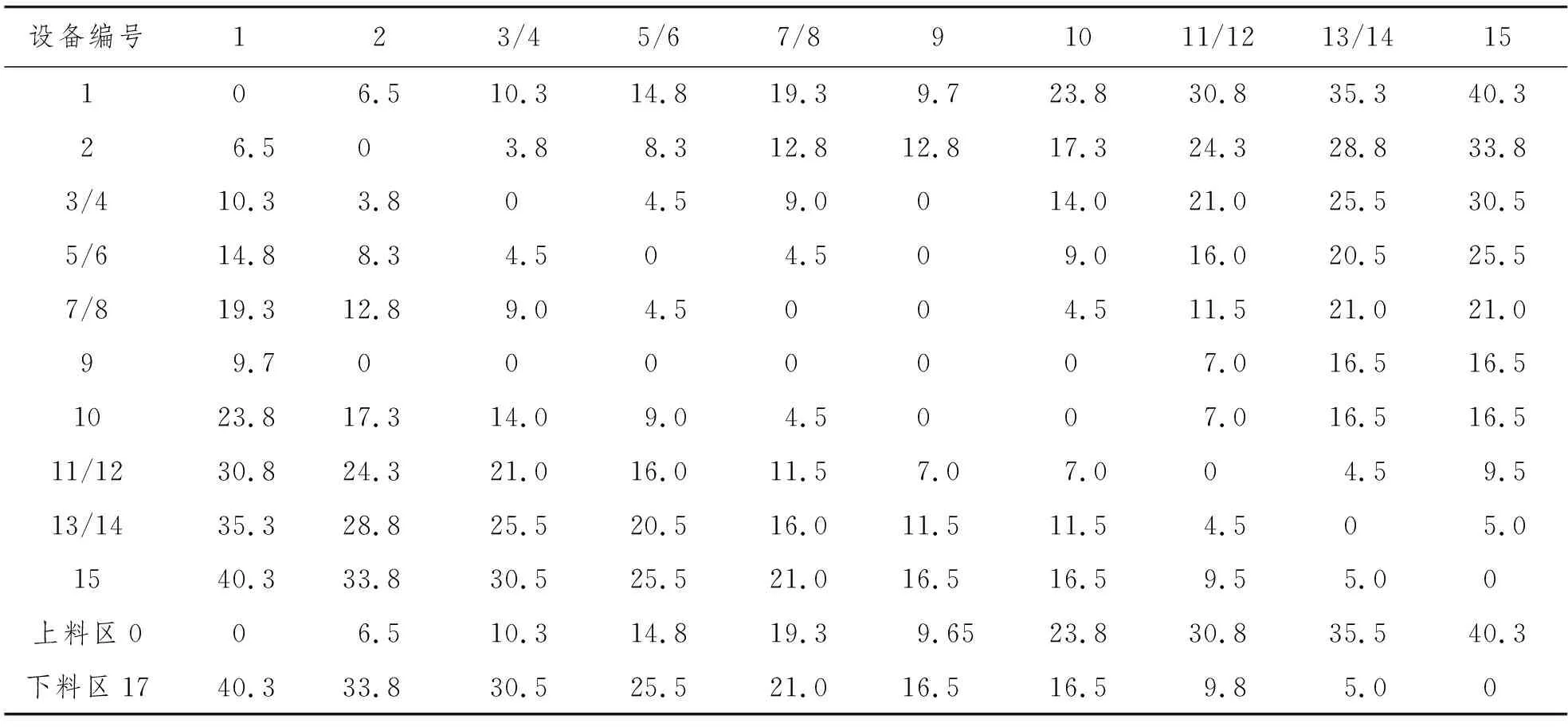
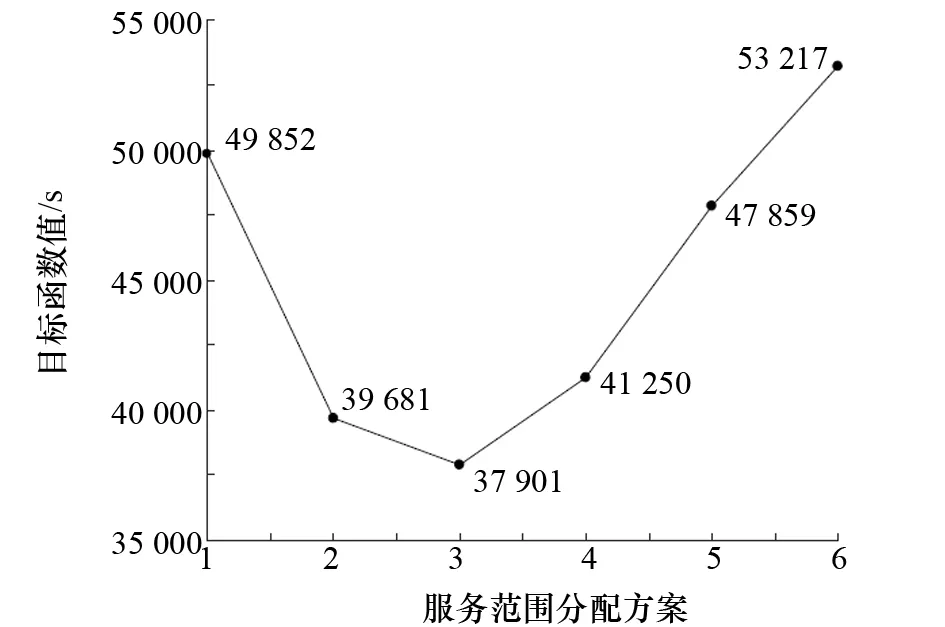
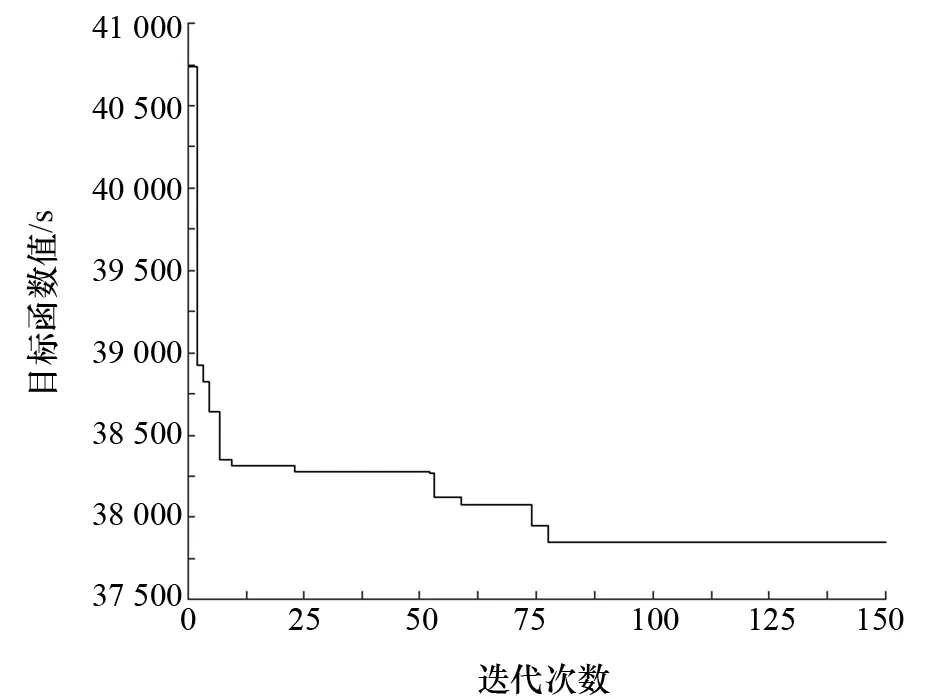
(9) 若d

(10) 若d=D且k

(11) 解码最优解，给出最小调度时间。

4 实例分析

4.1 实例描述

以某企业动力电池生产线容量确定单元为例，对其进行设备加工任务分配、机器人任务分配和路径优化。容量确定单元由1 V放电、容量确定前充放电、容量确定、静置、补充电和分拣等6道工序构成，该单元因各工序加工时间较短，设备数量较少而形成了多工序加工单元。各工序加工时间与设备数量如表2所示。

表2 容量确定单元工序信息

4.2 容量确定单元服务范围分配方案

在初始参数设置上，设置交叉概率Pc=0.8，变异概率Pm=0.1。种群规模P=100，最大迭代次数D=400，机器人数量2台，以完工120件电池盒为计算目标。

工序约束矩阵为：G={G1,G2,G3,G4,G5,G6},其中：G1={1}表示1 V放电工序，其设备为1号；G2={2,3,4,5,6,7,8}表示容量确定前充放电工序，其设备编号为2～8号；G3={9}表示静置工序，其设备编号为9号；G4={10}表示容量确定设备，其设备编号为10号；G5={11,12,13,14}表示补充电设备，其设备编号为11～14号；G6={15}表示分拣设备，其设备编号为15号。缓冲区设备表示为：B={B1,B2,B3,B4,B5}={20,9,21,22,23}。取机器人平均速度为1 m/s，上下料抓取时间10 s。各设备间机器人行驶时间表H按表3输入。