基于牵制控制带有协议失效多智能体的一致性

王国良，孙媛媛

（辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001）

多智能体系统是许多动态系统的集合，其中网络拓扑通常被建模为节点图。点表示多智能体，边表示多智能体之间的关系。其目标是把一个庞大而复杂的系统变成一个小系统，可以互相通信和协调，同时也易于管理。此外，多智能体系统被广泛应用于智能机器人、交通控制、柔性制造、协调专家系统、分布式预测、分布式智能决策以及其他领域。到目前为止，关于各种多智能体系统的研究成果有很多，如稳定性分析[1]、同步、故障检测[2]等。相关的控制问题有非线性切换[3]、滑模控制[4]、分布式控制[5]、分布式群集控制、H∞控制等。

多智能体系统的一致性问题在生物、物理、控制等领域有着悠久的历史并受到广泛的关注[6]。当网络上的所有多智能体系统都收敛到一个共同的状态，即多子系统达成一致或具有一致属性。这是一个基本的协同控制中的问题，与同步问题密切相关。在过去的几十年里，一致性问题在网络化控制系统、时延系统、非线性系统等系统中的应用都取得了很好的结果[7]。以上研究大部分基于一种理想的假设，即网络拓扑是固定的，并且始终可用。然而，在实际应用中，系统受到环境的影响可能导致临时控制器失效，耦合矩阵发生突变[8]。对于具有切换拓扑的系统，可以采用平均法处理快速切换情况，也可以考虑对两个一致问题的离散多智能体系统研究。当切换具有一定的随机性，通常将其建模为马尔可夫过程[9]。虽然相关网络拓扑经历了随机变化，但不能描述耦合中存在的故障情况。换言之，切换只发生在有效的网络拓扑之间，对于多智能体系统在随机损耗的通信网络的研究较少。通过引入伯努利变量，给出随机网络一致的必要条件[10]。在相似的网络拓扑下，可对多智能体系统一致性的最大允许损失率进行了研究。由此可知伯努利变量是一种表示连接失效常见的方法，驻留时间都具有随机性，状态的切换非常快，其驻留时间通常很短甚至是瞬间的。这种现象也能在具有马尔可夫跳变的网络拓扑结构的多智能体系统中发现，但对于实际应用非常不利。因此，对于通信拓扑连接有效与否的相关问题的研究非常有意义。此类研究不能直接应用之前的方法或结果。多智能体系统的研究大多采用分布式控制的方法，每个节点都相对应添加一个控制器来实现一致性。虽然控制器相关部分的效果较好，但不易实现，尤其是多智能体数量非常大的时候，在实际应用中控制每个智能体比较困难。相反，根据牵制理论[11]，对于具有多智能体系统减少对应的控制器也可以显著地实现同步。但是，这类研究很少考虑多智能体系统在协议失效时的牵制一致性问题。

本文研究了多智能体系统的一致性问题，其中所设计的控制器为牵制控制器，系统在一段时间协议有效，一段时间协议失效。构建了一种协议失效网络，并将驻留时间作为一个常数加以考虑，以此确定一致控制的前提条件，在包括N 个节点的情况下，基于网络连接有效的李雅普诺夫函数或者网络连接失效的李雅普诺夫函数进行一致分析，以获得简洁的条件。构建了一种牵制控制器，并给出其存在的两个建立条件。此外，还将对这些条件进行比较,与传统牵制控制相比，考虑了多智能体之间连接失效的情况，控制方法具有更广泛和一般性的应用前景。

1 问题描述

考虑带有N 个节点的多智能体系统，节点的动态方程为：

式中，xi(t)=[xi1,…,xin]T∈Rn是i 节点的状态变量，其中n 为系统的个数（n ≠N）；N 为节点的个数；ui(t)∈Rm为控制输入；A、B 为带有可兼容维度的已知实矩阵。假设耦合矩阵G=(gij)∈RN×N是无向可连接并且满足

然而，耦合矩阵并不是实时存在，意味着有时节点之间连接失效，这种情况的状态方程可以描述为：

定义1 τ=t2n+1-t2n,n ∈N 表示连接有效的驻留时间；相反，φ=t2n+2-t2n+1,n ∈N 表示节点连接失效的驻留时间（N 为全体非负整数）。用一个随机变量α(t)表示耦合网络存在与否。

系统（1）可表示为：

根据克罗内克乘积性质，系统（1）还可表示为：

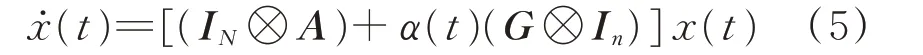
注释1 模型（5）与现有的相似模型不同。更具有一般性，并包含一些现有的特殊情况。首先，引入的变量α(t)与文献[12-13]的驻留时间的形成是不同的，α(t)为伯努利变量，其驻留时间非常小或者是瞬时的，而模型（5）的驻留时间有两个常值的情况。其次，当α(t)≡1，所描述的情况与文献[14]描述的类似，没有发生连接故障。特别地，当引入的变量约简为一个传统的伯努利变量时，系统（4）将变为一个类似于文献[12]的随机损耗网络。

定义2 当节点之间满足如下关系，多智能体系统实现一致性。

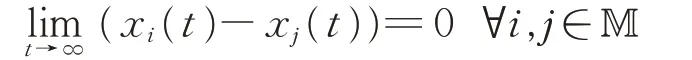
引理1 对于任意实矩阵A∈Rn×n和正定对称矩 阵P ∈Rn×n，任 意 标 量ς 满 足其中λmin(P)、λmax(P)分别表示正定对称矩阵P 的最小、最大特征值。则可以得到：

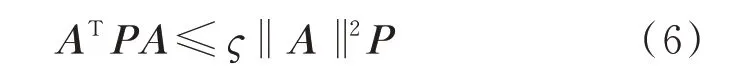
更多的，还要满足条件（a）、条件（b）其中之一：（a）P≥I，P ≤ςI；（b）P ≤I，ςP≥I。则条件ς≥可被条件（a）和条件（b）取代。

证明对于任意的实矩阵A∈Rn×n和P ∈Rn×n满足P＞0，可得：

特别的，当P≥I，可以得到λmin(P)≥1。更多的，对于P ≤ςI，则有ς≥λmax(P)，可得：

另一方面，当P ≤I，可以得到λmax(P)≤1，至于ςP≥I，则ςP≥ςλmin(P)I≥I，可得：

基于以上情况，不等式（6）在满足条件（a）或条件（b）之一的情况下成立。证明完毕。

引理2[14]对于任意矩阵A，则：

2 主要结果

定理1 对于给定的标量ς＞0，存在矩阵P1＞0 和P2＞0 满足其中如下一个条件，则系统（5）能够到达一致。

和

标量α 和β 与矩阵A 有关，通过引理2 可求出。

证明因为节点网络为无向可连接图，存在一个正交矩阵U ∈RN×N以及一个对角矩阵：

式中，λ1=0，λi＜0,i ≠1。令：

系统（5）可以转变为：

还可以转变为：

基于等式（18），可以看出x(t)和x͂(t)的稳定性是相同的，至于系统（20），得：

通过计算可得：

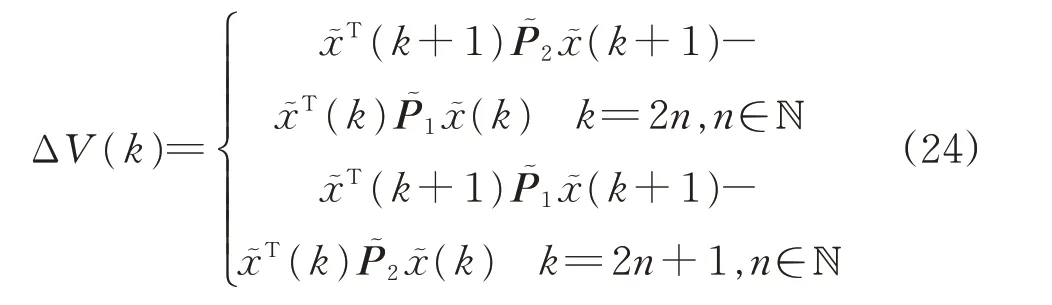
式 中，ΔV(k)=V(k+1)-V(k)；P͂i（i=1,2）定义为：

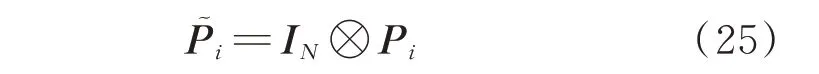
当k=2n，可得：

基于条件（13）或条件（14），通过引理1 可得：

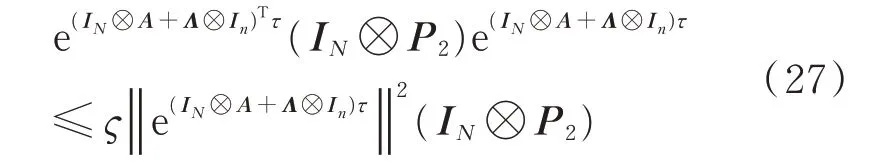
由于(IN⊗A)(Λ⊗In)=(Λ⊗In)(IN⊗A)，有：

进一步可得：

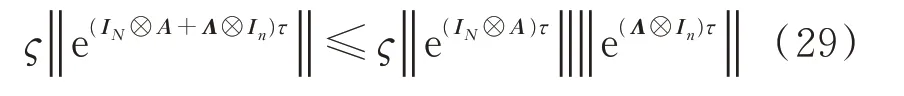
从条件（17）可得：

基于引理2，矩阵H͂可以被写成H͂=(IN⊗H )，可得：

等同于：

基于式（30）和式（32），可知：

参数α 和β 在引理2 中给出。计算可得：

以上不等式可通过条件（15）保证。对于k=2n+1，基于可得：

意味条件（16）成立。进而ΔV(k)＜0，∀k ∈N满足V(k)＞V(k+1)＞…＞V(k+n)＞…总结得：

更多的可得：

式中，γ=mini∈{1,2}{ λmin{ P͂i}}＞0，意味着：

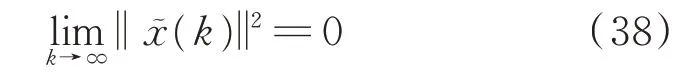
则系统（22）为随机稳定，基于式（21）可得：

注释2 由系统（5）可知其维度为Nn，当与维度N 相关的节点数量较大时，构造的李雅普诺夫函数得到的结果非常复杂。此外，变量的维度和待求解的LMIs 非常复杂。然而，在定理1 中计算的复杂度大大降低，变量和LMIs 求解条件只与n 有关。

注释3 虽然驻留时间τ 和φ 为常数，但基于定理1 可以很容易地扩展到时变的情况，通过考虑条件（15）和条件（16）的单调性可以得到τ(t)≥τmin、φ(t)≤φmax。基于上述定理，可以设计一种基于多智能体系统(1)的牵制控制器，具体形式为：

其中，设计ki＞0，α(t)从式（3）可知。将矩阵B 定义为单位矩阵，则更具有一般性。Sℓ定义为将其代入于式（1）可得：

定理2 对于给定的标量ς＞0，如果存在标量ki＞0，i ∈Sℓ和矩阵Pi＞0 满足条件（13）或条件（14）其中之一和条件（16）以及条件（42），则控制器（40）可以使系统（5）实现一致性。

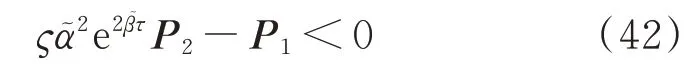
证明由于耦合矩阵G 不可约，秩为所有的特征值为负。有一个正交矩阵U ∈RN×N和一个对角矩阵为：

其中，λi＜0。不失一般性的，将λ1看成最大特征值，对于系统（41）可得：

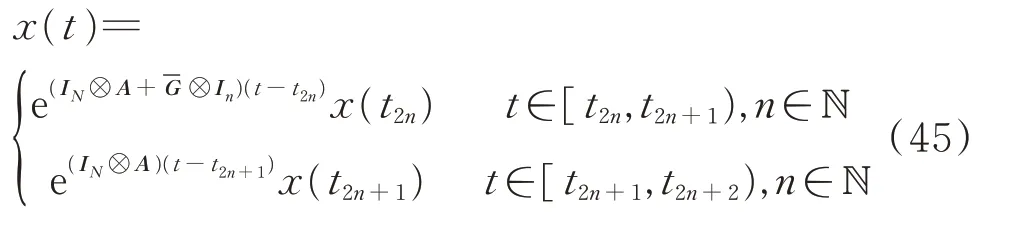
基于引理1 可得：

同样的，根据引理2 和矩阵H͂可得到式（43），则进一步得：

定理3 如果有一个给定的标量ς＞0，存在标量ki＞0，i ∈Sℓ以及矩阵Pi＞0 满足条件（13）或者条件（14）其中之一和条件（16）以及条件（50），则带有控制器（40）的系统（41）能够实现一致。

其中，参数α 和β 在定理1 中可知，λ1是的最大特征值。

则式（34）转化得：

余下步骤与定理1 的证明相同，证明完毕。

注释4 定理2 和定理3 对于设计控制器（40）都是有效的。由于分别采用不同的计算方法，计算的稳定性和复杂度也有所不同。在定理2 中，条件（48）通过完全考虑得到。相反，不等式（51）只与的最大特征值有关，后者保守性更小并且计算复杂度较小。因此，应该在具体情况下考虑使用哪一种方法。特别是，当ℓ=1 时，多智能体系统（1）可以通过选择一个固定的控制器来实现一致。

3 仿真算例

考虑一个多智能体系统，其智能体是一个沿俯仰轴的卫星运载火箭[15]。其状态空间模型为：

式中，xp1为俯仰角，（°）；xp2为俯仰速率。本算例中，多智能体系统由一个固定一致控制器(40)来稳定。假设线性多智能体系统有5 个节点，多智能体系统节点的耦合关系如图1 所示。

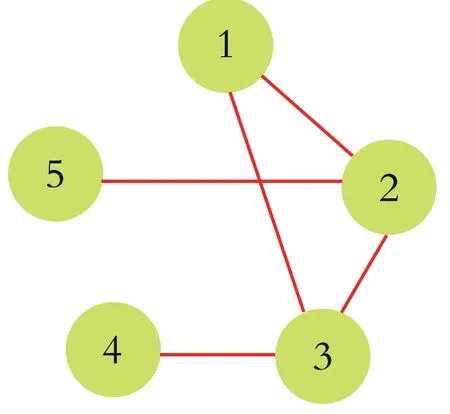
图1 多智能体系统节点的耦合关系

多智能体系统节点的耦合关系可表示为：

在每个节点初始条件x0=[11]T相同的情况下，应用上述设计的牵制控制器，系统(5)描述的状态响应曲线如图2 所示。仿真结果表明，所提出的牵制控制方法是有效的。

图2 带有牵制控制器的系统（5）状态响应曲线

其中，k2min是对于不同τ 值的参数k2可允许最小值；ς=10。此外，从式（50）可知，λ1值越小，参数k2越大。因此，牵制控制器的驻留时间越大。仿真结果可以看出，在定理3 的情况下，当参数ς ＜1.01，τ=10，参数k2是无解的。

图3 k2min 跟随τ 的变化曲线

基于这样的情况，可以考虑牵制更多的节点，如节点1 和节点2，当k1=1 和k2=1 时，可以实现一致目的。从算例中可以看出，牵制不同节点可以产生不同效果，具体情况要具体考虑。

4 结 论

研究了带有协议失效的线性多智能体系统的一致性，构建了一种牵制控制器来实现这一目标。与传统的方法相比，网络节点连接成功或失效的驻留时间并不是瞬时的，驻留时间长度的大小情况得到了充分的考虑。采用了包含两种情况的李雅普诺夫函数得到简洁且计算量小的结果，并利用一些新方法最终实现了一致性的目的。最后，通过实例验证了所得到结果的实用性。