Scalable Clock Synchronization Analysis:A Symmetric NoncooperativeOutput Feedback Tubes-MPCApproach

Ting Wang, Xiaoquan Xu,and Xiaoming Tang

Abstract—In the cyber-physical environment, the clock synchronization algorithm is required to have better expansion for network scale. In this paper,a new measurementmodel of observability under the equivalent transformation of m inimum mean square error(MMSE) is constructed based on basic measurement unit (BMU), which can realize the scaled expansion of MMSEmeasurement. Based on the state updating equation of absolute clock and the decoupled measurement modelof MMSElike equivalence, which is proposed to calculate the positive definite invariant set by using the theoretical-practical Luenberger observer as the synthetical observer, the local noncooperative optimal control problem is built,and the clock synchronization system driven by the idealstateof local clock can reach the exponential convergence for synchronization performance. Different from the problem of general linear system regulators, the state estimation error and state control error are analyzed in the established affine system based on the set-theoryin-control to achieve the quantification of state deviation caused by noise interference. Based on the BMU for isomorphic state map, the synchronization performance of clock states between multiple sets of representative nodes isevaluated,and the scale of evaluated system can be stillexpanded. After the synchronization is completed, the state of perturbation system remains in the maximum range of measurement accuracy,and the state of nom inal system can be stabilized at the ideal state for local clock and realizes the exponential convergence of the clock synchronization system.

I.In t roduction

W SN(w ireless sensor networks) network scale is expanding,the needs of a large number of cyberphysical applications for high-performance clock synchronization algorithm are also increasing[1].However,due to the dynamic change of communication between nodes,WSN channel conflict,time-varying channel gain and other unreliable transm ission factors,in the face of more stringent complex real environment,the clock synchronization application presentsa greater challenge.

The engineering background of the paper is reflected in whether the convergent performance of the clock synchronization can be realized independently of the size of the network scale.It can analyze the convergence speed and convergence error quantitatively,which is usually of important practical significance for determ inistic industrial applications(industrial applications for hard real-time),internet of things(IoT),and 5G.For example, the on-line monitoring and acquisition of synchronousdata for large-scale rotary intelligent equipment.

Early clock synchronization studiesused thew irelesssensor network time synchronization protocol based on the hierarchical structure to estimate clock parameters and synchronize adjustments,such as timing-sync protocol for sensor network(TPSN)[2],reference broadcast synchronization(RBS)[3],flooding time synchronization protocol(FTSP)[4],and so on.The clock synchronization protocolhas good performance on a small network.W ith the development of technology,the network size expands exponentially,and the protocolalgorithm can not meet theenergy constraintsand the constraints of computation consumption.Consensus technology is gradually used for clock synchronization,such as average timesynch(ATS)[5],asynchronous consensus algorithm[6],maximum time synchronization(MTS)[7],and so on.Inspired by the ATS,[8] proposed a novel synchronization protocol,denoted as robust average timesynch (RoATS),to adjust both the nodes’clock frequency and clock offset in a robust way w ith respect to bounded communication delays.In[9],a broad fam ily of random ized clock synchronization protocols based on a second order consensus algorithm are proposed.It is proved that the parameters of the algorithm can always be tuned in such a way that the clock synchronization is achieved in the probabilistic mean-square sense.In[10],the clock synchronization problem for event-driven measurement applications is addressed based on the consensus-based protocol and prelim inary version of the RoATS-like.The relative clock modelas a coupled statemodel depended on the average of the interactions to achieve the synchronous compensation or cooperative control process.Therefore, both of the existing protocols and average methods of consensus were lim ited by the scale of network,and w ith the expansion of network scale,the convergence performance of clock synchronization w ill decrease.

In recent years,the clock synchronization has beenmainly studied using the statistical signal processing framework[11].The researchers realized that clock synchronization was essentially a parameter estimation problem.The WSN clock synchronization was analyzed by using the statistical signal processing perspective,and the performance of some classical protocolswasevaluated under different network random delay distributions in [11].

The parameter estimation of clock synchronization w ith processing of statistical signal studied the clock parameters’estimation of different delays and protocols in a unified framework.However,under the scaled expansion of network,based on the synchronous compensation of relative clock model,the convergence for parameter estimation of clock synchronization w ill decrease.Itwas still difficult to quantify and evaluate theestimation errors.

Recently,consideringmessage delays are not considered in the research of clock synchronization in sensor network,which causes largemean-square-error unconverged clocks,a fully distributed clock offset and skew tracking algorithm using the Kalman filtering was proposed.The Kalman filtering was used in[12]to derive amessage-passingmethod(two-ways-message exchange)for the clock offsets tracking in the presence of message delays.We need to further expand the researching results of the international scholars who have made achievements in the study of time delay.Specifically,delay has been extensively studied,such as[13]and[14].In fact,the clock model in[12]has a new and different nature(the state of node depends on the “noise disturbance”of its own node in state spacemodel).Therefore, by combining the modeling of statistical signal processing w ith the quantitative evaluation framework of networked control theory,we proposea new viewpoint of research.

The relative clock model as a coupled state model depends on the cooperative control process.The convergence rate of consensus-based method of clock synchronization is lim ited to network size focuses on convergence(stability),which is difficult to quantify and analyze convergence rate,especially for unreliable networks.The interaction of network communication information w ill consume a large amount of energy,and affect w ireless network life cycle.

For the proportional-integral(PI)controller[15], we could know that when the node isdormant or thenew node joins the WSN,it is needed to rebuild the spanning tree or cluster topology,so itwas notconducive to the expansion of network scale.On the other side,in relative clock model including relative reference node among agents,a second order consensus algorithm[9]employed randomized synchronization communication protocol coupled w ith a PI control at each agent.It was possible to properly tune the linear PI-like control so that the network achieved clock synchronization.

The absolute clock model in[12]is modeled as the decoupling state model, but the measurement model(using message-passing method in two-way-message exchange)is still the auxiliary measurement process of absolute state,and there is actually a state coupling relationship.It is found through the analysis that [12]cannotmeet the observability of the system.Therefore,we propose the problem of the observability for the modelof theabsolute clock.Based on the framework in[16]and[17],the present paper constructs the measurement model of observability of BMU under the transformation of m inimum mean square error(MMSE),which meets the necessary conditionsof the state’sestimation of system.

The superiority of predictive control in dealing w ith the industrial constraint problem brings together the advantagesof distributed model[18].Therefore,this is an effective way to solve large-scale clock synchronization problems for cyberphysical applications.Instead,scalable solutions are those solutions whose clock synchronization performance is independent of the system size.Distributed model predictive control(DMPC)algorithm[19]like the cooperative consensus-based method can be used for the solution of synchronization problems of both linear and nonlinear systems.However,it neither take into account the noise perturbation, nor has output feedback that is an important characteristic for clock synchronization and does notadapt to network size.Inspired by the previous work[20],[21]have addressed the DMPC for a set of linear local systems w ith decoupled dynam icsand a coupled global cost function.

In the industrial cyber-physical networking(including w ireless smart devices embedded in w ireless RF chips),the present paper aims to further improve the clock synchronization enhancing DMPC when considering[22]–[24]on robust and stochastic MPC.On the basis of solid theory,we need to pay more attention to the applicability research of MPC in the specific application fieldmodel[22].The on-line synthesis approaches of MPC have been investigated for networked control systems(NCS)where the packet loss and data quantization are coexisting(see[25]–[27])and networkinduced delays(see[28]and[29]),and it is the one which guarantees the closed-loop stability,i.e.,the closed-loop system is stable whenever the optimization problem is feasible.See[30],[31]for the latest relevant researches for the problem of trajectory tracking under complex constraints.In present paper,we turn the clock synchronization adapted to scalable networks into a set-point tracking problem and design a DMPC to drive the clock parameters of each node to a common ideal clock statesZ.

The standard method of obtaining unbiased parameter tracking in MPC is to add a perturbation system model to the prediction modeland then use an observer to estimate the real perturbation.Maeder and Morari provide a method of perturbation estimation for any unstable system model in[32].The key point of thismethod is that the selected perturbation system model should meet the internal model condition and the target tracking conditions in the MPC problem are not appropriate for the clock synchronization problem.Other method are robust MPC(RMPC)and stochastic MPC(SMPC).On RMPC, the disturbances are assumed to be bounded and constraints are required to be satisfied for all possible realizations of the disturbance process.In SMPC,on the other hand,disturbances are assumed to be stochastic and not necessarily bounded and(at least some)constraints are softened,i.e., not required to be satisfied for all realizationsof the disturbance[24].Reference[22]comprehensively studies the importance of robustness and stochasticmodel prediction control, points out that the research of model predictive controlneeds to fully consider the industry demand,themain concern is the robustand stochasticmodel predictive control,because these modal MPCs often need to solve complex online optimization control problem.It is pointed out thatwe should consider the further expansion of the Tubes method,and the terminal domain constraints should also be further considered to exploit theMPC advantage.

The distributed control algorithm studied has exponential convergence,so as to realize the large-scalemulti-point online monitoring of “Industrial IoT”under smart manufacturing.

The main contributionsof this paper are:

1)Based on the previous research[16],[17], this paper constructs an observable measurementmodelunder the BMU for absolute clock in the large-scale network from the viewpoint of networked control theory;

2)Aim ing at the calculation problem of positive definite invariant sets,the observability measurement model of MMSE-like equivalence is proposed to calculate the positive definite invariant set by using the Luenberger observer as the synthetical observer.Then the on-line calculation of the Tubes-MPC method for clock synchronization can be realized;

3)Using the feedback control strategy and set-theory-incontrol to establish the control error positive definite set,quantitatively analyzing the deviation between the estimated system state and the nom inal system statew ith ameasurement model of observability.The exponential stability convergence performance of Tubes-MPC for clock synchronization is achieved;

4)The determ ined estimated value of the absolute state by using the equivalent observability measurement model of MMSE is based on the ideal state as public reference target.The problem of clock synchronization is transformed into the problem of set-point tracking to ideal state for local clock.

II.Clock Synch ronizat ion System/Framework Based on Netw orked Cont rol Perspective

Fig.1 describes the main modules involved in the clock synchronization system.In this paper,The clock synchronization is carried out according to the above procedure.There is no specificity between the nodes.The processmainly involves:

4)Clock Parameter Estimation

Estimator:Due to the different network environment of different nodes,each node may have differentmeasurement quality,and because of the presence of noise in the measurement process,the state is polluted.According to the

Fig.1.A distributed absolute clock synchronization system framework based on networked control perspective.

For each node w ithin the WSN,repeat the above process,the cumulative clock offset of each node and the estimated value of the clock skew are approaching the state target,and tend to the standard reference time,that is, to achieve distributed clock synchronization.

It is proved that clock synchronization model based on control also applies to the separation principle(“3.Control Strategy in Clock Synchronization”in[16]).For the state estimator and controller design in Fig.1,a separation principle is proposed to decompose the controller of the stochastic control system into two parts:state estimation and determ inistic feedback control[16].When applying this principle,the state of the system is estimated based on the random observation data,and then the estimated value is regarded as the real state.The optimal control law is designed according to the deterministic system.Reference[16]proposed the stochastic optimal control of the networked control perspective based on the relative clock state space model.



III.Dist r ibu ted Upda ting M odel of Absolu te Clock Sta te Based on Networked Cont rol

The absolute clock statemodel is established by analyzing the underlying hardware clock counting error.According to the discrete clock reading model in[12],the optimal control quantityis updated, then the logic clock reading value is updated in each sample cycle. After adding the control decision, the iterative relationship of the clock read is

Fig.2.Clock synchronization cycle.

IV.Loca l ized Obser ver Design

A. Local Observation Model

Since the clock state of the node can not be obtained directly,it is necessary to observe the clock state of the node by means of its neighbor node,we construct the observer to estimate the clock state.This section gives two local clock stateobservation models.

We use two-way time-stamp exchange based on the senderreceiver,so that the delay induced by the network can be categorized into the random delay in the observation.

1) Proposal of Problem

According to the detailed analysis in Appendix A,a state spacemodelof the system clockmade up of themeasurement model of the system established by using themechanism of two-way message exchange and the state-decoupled state transition equation cannot meet the observability of the system state in [12].

Fig.3.State vector space for absolute clock model.

Fig.4.A set of clock information exchange processes ( and are symmetrical measurement information each other).

2) Analysisof Physical Process,Strategy and Transformation of MMSE Equivalence

According to the modern control theory,in order to determ ine the internal state of the system through measurements,it is the key to ensure the observability of the system that needs correctly selecting the appropriate measurement model.For this purpose,we introduce a BMU to study the nature of physical process of two-way message exchange in depth and establish an auxiliary measurement model of theabsolute clock.

W ith the help of the auxiliary measurement model,the relative measurement model in[12]is transformed into a decoupled equivalent measurement model w ith MMSE performance through a linear transformation,consequently the observability of the system can be ensured.Referring to the process of this equivalent transformation,a modified Luenberger observer is constructed and an upper bound of its error covariance exists.This is described as the follow ing Theorem 1.

Theorem 1:Considering(19)–(21),and(25),the observability of BMU has established the necessary conditions for equivalentmeasurement of MMSE:Equations(19)–(26)are established to represent the evolutionary cues of observability in measurement model of the system.Under the analysis model of the BMU,an auxiliary measurement model conforming to the physical process is constructed.Through the equivalent transformation for measurement of MMSE,a measurement model for observability of the subsystem is established to realize theobservability of the subsystem.

It is proved that “equivalent transformation of MMSE performance”indicates that the independent measurement noise in(21)is converted here into the correlated measurement noise.The MMSE-like measurement can be performed using the distributed Luenberger observer(The MMSE measurement can be performed using distributed Kalman filter,and see Appendix C for proof).

Proof (Strategy of Observability):Clear demonstration for observability of BMUs can be seen in Appendix B for details.This section serves asa refined version of the follow ing proof to help usunderstand the key detailsand major points.

B. Low-Complexity Luenberger State Observer(MMSE Measurement Equivalence—Theoretical Observer)

Proposition 1:Due to the observability of observer is the necessary condition for equivalentmeasurement of MMSE,when we perform the MMSE-likemeasurement equivalence,the proposed alternatives can be traded the between online controllersand replaced by offline optim ization.

Using the decoupled observation model(25)and the coupled observation model(21)established in the previous section,the decoupled observer and the coupled observer can be established,respectively.

In fact,based on themarsurement accuracy of the Kalman filter in[12],we have carried on the indepth analysis to the equivalent transformation of the MMSE in the observer measurement.Different from[12],it has been strictly proved that the equivalent transformation of MMSE which satisfies observability exists in the distributed Kalman filter w ith the state-space model of absolute clock.

Based on the theoretical analysis of the equivalent transformation of MMSE,the decoupling measurement can be realized in the equivalent transformation of MMSE through two-way message exchange(as shown in Appendix B,observability can be achieved.).Considering the characteristics of the Luenberger observer w ith low computational complexity,weusea Luenberger observer.

Considering the state space(7)of the system and the decoupled observation model(26),we can build a decentralized Luenberger observer

C. Low-Complexity Luenberger State Observer(MMSE Measurement Equivalence—Practical Observer)

Proposition 2:Reversing reconstruction from relative state to absolute state estimation,online measurement is regarded as theMMSE-like measurement equivalence.

Considering the state space equation(7)of the system and the coupled measurement model(22),a distributed Luenberger observer can be established.The coupled measurement equation(22)deals only w ith the states of its own node and all neighbor nodes.The standard Luenberger observer isdecomposed into a distributed form

V.Design of Dist r ibuted Clock Synchroniza tion Quant ita tive Ana lysis System Based on Tubes-MPC

In this section,wemainly discuss the controldecision based on the parameter tracking,and propose a distributed Tubes-MPC clock synchronization algorithm based on thenetworked control perspective to realize the fully distributed clock synchronization which does not depend on special reference nodes.

Use a recent review[24]and a recent paper[33]on model predictive control in industry.Reference[22]emphasizes that many proposals for robust and stochastic model predictive control are probably too complex for current implementation in the process industries where most applications are to be found and to encourage the development of simpler alternatives.These simplifications employ nom inal predictive control w ith tightened constraints; the tightened constraints are determined offline using possibly extensive,stochastic optim ization[34].The alternatives are allbased on tube based model predictive control[35]–[37].In the paper,the alternatives as online controller strategies are based on specific absolute clock model.

Theorem 2:Simpler online controllers employed nom inal model predictive control w ith tightened constraints steer nom inal states to converge to common ideal statew ith exponential speed,and clock states(skew and accumulate offset)are centered on the nominal states,when the state tracking are independent between nodes(detail proof see the SectionsV-A and V-B).

According to the analysis of Section IV,it is different from the strict discussion of the general linear system in[38].In otherwords,it is applicable to the characteristics of the clock state space evolution model,and the deep understanding of the clock synchronization problem,the discrete time affine timeinvariant system model isestablished for the node.

A.Tubes-MPC Design of Affine System Based on Origin

Corollary 1 provides usw ith the necessary theoretical basis for obtaining the output feedback model predictive control of the original perturbation system.It has been known that the Tubes-MPC is studied for general linear systems in[38].Due to the particularity of the clock synchronization problem,the relationship(2) between the cumulative clock offset and the instantaneous skew leads to the introduction of the offsetin the state space equation(7).We study the Tubes-MPC algorithm for the clock synchronization affine system.In order to obtain the control strategy which meets the requirements,the Tubes-MPC method of the affine system based on origin is designed,and then extended to the Tubes-MPC method based on the set-pointto solve the clock synchronization problem.The Tubes-MPC also uses the initial state of the nom inal system as a decision variable so that the optimal control problem is closely related to the traditional optimal control problem that only the control sequence is taken as the decision variable in terms of the properties of the objective function.The traditional optimal control problemhas no uncertainty. According to Corollary 1,in order to ensure that the perturbation system satisfies the original constraint(33),has a constraint that is tighter than the original constraint,whereis the current state andis the prediction domain,and the control domain is.Define problemPN(x¯):

B.Tubes-MPC Design of the Affine System in Set-Point Tracking to Ideal State for Local Clock

Section V-A discusses themore common origin-based state tracking problems.However,the clock synchronization problem driven by the ideal state is essentially a set-point tracking problem.This section w ill continue to discuss the design of the Tubes-MPC under the clock synchronization problem based on the above basic conclusions.

For a clock synchronization affine system w ith an ideal stateZas the target

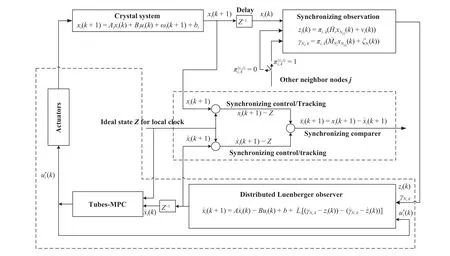
Fig.5.A block diagram of distributed absolute clock synchronization system based on networked control perspective.

C. Robustness of Tubes-MPC Clock Synchronization Algorithm

VI.Clock Synchroniza tion A lgor ithm Based on Outpu t Feedback Model Predict Con t rol

TABLE I Clock Synch ronization A lgor ithm Based on Output Feedback Model Predict Cont rol

VII.Simu lat ion and Per formance Eva lua tion

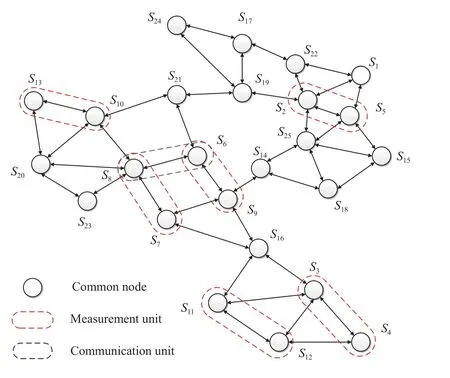
Fig.6. Network topology.

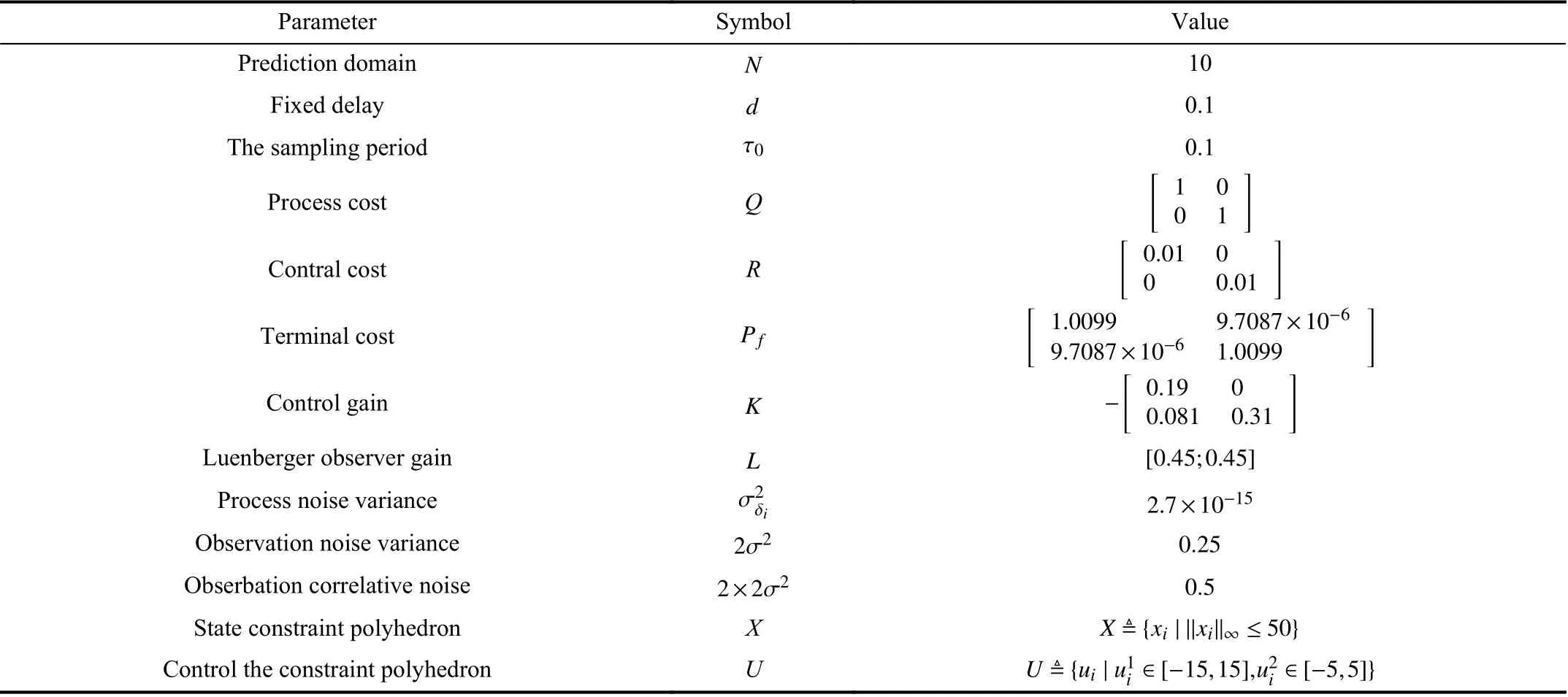
TABLE II List of System Parameters

Fig.7.State tracing trajectory based on quantization boundary constraint driven by set-point.

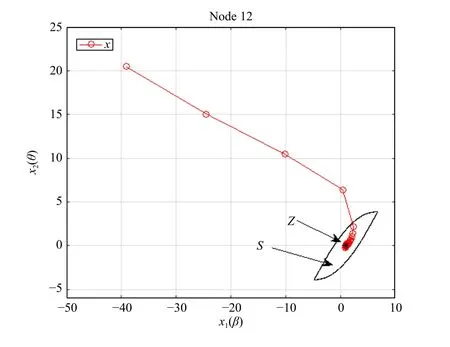
Fig.8.Single-nodeoriginal disturbance system state trajectory.

Fig.9.System states and control variation chart.

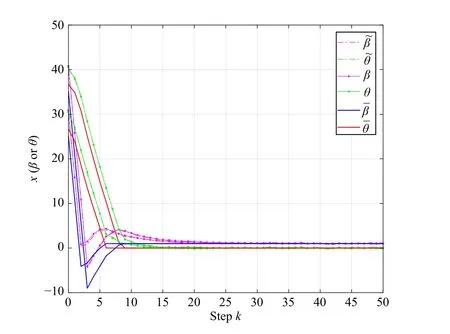
Fig.10.Different initial points clock parameter variation chart.

Fig.10 shows that the state sequences of the systems w ith the same nodes at different initial points have the same downward trend,which is the result of implementing the same control law.In order to reflect the dependency of the Tubes-MPC on the initialvalue of the state,and more clearly observe the state trajectory after the clock synchronization,we take different clock initialization states parameters and reduce the distance between the initial state parameter and the ideal state.It shows that nodes w ith different initial points are driven to the setwhere the initial parameter deviates from the ideal state,and the disturbance state continues to converge to the small range of targetZafter the disturbance system state enters the set,asshown Fig.11.

Fig.11.Tubes-MPC control trajectories at different initial.

Fig.12.Tim ing diagram of each system stateunder Tubes-MPC.

In Figs.12(a)and 12(b),it is clear thatall nodes have clock synchronization after 15 times synchronizations in the case of a large initial parameter difference,indicating that the Tubes-MPC is the initial parameter and there is no dependency relationship.At the same time,Figs.12(a)and 12(b)also show at the differentstarting points the system is driven to the invariant setw ith the exponentialspeed.It isknown that when the node clock skew is 1,it reduces the clock offset deviation between the nodes in the non-synchronization time,for more intuitively display clock synchronization between nodes,as shown in Figs.13(a)and 13(b)which reflect synchronization trend between clock readings among nodes.In this paper,it is considered that the clock reading deviation between nodes is no more than,which means that the clock synchronization is achieved.Since the system state w ill change,the node clock readingsw ill still occurw ithin a small range of deviation, but they are w ithin the allowable range.

Fig.13.Clock readings.

Figs.14(a)and 14(b)show the exponential convergence of the system state for all nodes under different sampling periods.Figs.15(a)and 15(b)show the clock readings of all nodes under different sampling periods,revealing synchronization situation of all nodes.Figs.14 and 15 show that all nodes synchronize at the 15th step,revealing that the number of synchronization steps is not affected by the sampling period when the clock synchronization method synchronizes all nodes.The simulation results show that the clock synchronization method has some robustness to the sampling period,the relative size of the error invariantsetcan also be controlled by selecting an appropriate sampling period.

Fig.14.Tim ing diagram of each system state.

VIII.Conc lusion

Fig.15.Clock reading of all node.

In thispaper,a new exploration ismade from thenetworked control perspective,and a quantitative analysis and design method of clock synchronization problem based on the output feedback model predictive control is proposed.Based on the two-way information exchangemechanism of w ireless sensor networks(including w ireless smart devices embedded in w irelessRF chips),an equivalent decoupled observer model is proposed. An output feedback model predictive controller for the affine system is designed.The robust exponential convergence of the clock synchronization system is established,and the error synchronization set is used to quantize the clock synchronization parameter boundary.The symmetric noncooperative MPC method has network-scale adaptability.Based on the ideal state of the local clock,it calculates online and controls,therefore it has a smaller load of communication(the power consumption of the sensor node ismainly caused by the load of communication).Themethod has a certain degree of robustness to the sampling period;the output feedback model predictive control and the general model predictive control has the same computational complexity.

According to more strict proof,theexponential convergence for the state tracking method of clock synchronization designed by the proposed measurementmodel of the MMSE equivalent transformation of observability does notdepend on the expansion of network scale.The proposed method is suitable for the application of large-scale industrial Internetof Things.

Appendix A Proposa l o f Problem

Appendix B Proof of Observabil ity for BMU

Through the above study,it isknown that the system(67)is unobservable,and using the multiple sets of measurements can only determine the relative amountof clock state between the center nodeand the neighbor nodes.In order to determ ine the state of node,a self-statemeasurement model can be built by analyzing the mechanism of two-way information exchange for each node