Parallel Control for Optimal Tracking via Adaptive Dynamic Programming

Jingwei Lu,Qinglai Wei,,,and Fei-Yue Wang,,

Abstract—This paper studies the problem of optimal parallel tracking control for continuous-time general nonlinear systems.Unlike existing optimal state feedback control,the control input of the optimal parallel control is introduced into the feedback system.However,due to the introduction of control input into the feedback system,the optimal state feedback control methods can not be applied directly.To address this problem,an augmented system and an augmented performance index function are proposed f i rstly.Thus,the general nonlinear system is transformed into an aff i ne nonlinear system.The difference between the optimal parallel control and the optimal state feedback control is analyzed theoretically.It is proven that the optimal parallel control with the augmented performance index function can be seen as the suboptimal state feedback control with the traditional performance index function.Moreover,an adaptive dynamic programming(ADP)technique is utilized to implement the optimal parallel tracking control using a critic neural network(NN)to approximate the value function online.The stability analysis of the closed-loop system is performed using the Lyapunov theory,and the tracking error and NN weights errors are uniformly ultimately bounded(UUB).Also,the optimal parallel controller guarantees the continuity of the control input under the circumstance that there are f i nite jump discontinuities in the reference signals.Finally,the effectiveness of the developed optimal parallel control method is verif i ed in two cases.

I.INTRODUCTION

TREMENDOUS strides have been made in the past decades in the area of control theory and technology due to the development of science and computational capacity of computers,and the intelligent control is one of the most rapidly developing technologies recently[1]−[9].In the area of intelligent control,adaptive dynamic programming(ADP),proposed by Werbos[10],[11],is an effective technique to solve optimal control problems of nonlinear systems.Such optimal control problems are often required to solve a nonlinear partial differential equation called the Hamilton-Jacobi-Bellman(HJB)equation[12]−[15],and the analytic solutions of the HJB equation can not be obtained directly in most cases.Thus,the ADP technique emerges to obtain the solution of the HJB equation forward-in-time and has attracted much attention from researchers[16]−[26].In many cases,value or policy iteration is used in the ADP technique to solve the HJB equation.The difference between value or policy iteration lies in an initial admissible control,policy iteration method requires an initial admissible controller while it is not necessary for value iteration method[22],[27],[28].Recently,several online methods based on the Lyapunov theory are proposed to solve the HJB equation without sequential updates of neural networks(NNs)of the critic and actor[29]−[32].

In engineering applications,the tracking control problem is more common than the regulation problem[31],[33]−[35].Many intelligent methods including the ADP have been applied by many researchers to solve the optimal tracking control problem[36]−[39].In[40],a greedy heuristic dynamic programming(HDP)method with a new performance index is proposed for the discrete aff i ne nonlinear systems.In[41],a data-driven robust approximate optimal tracking control scheme is proposed for the unknown continuoustime nonlinear systems based on the ADP technique for the fi rst time.In[31],an ADP-based optimal tracking control method without using value and policy iterations is for the helicopter unmanned aerial vehicles.In[42],a data-driven adaptive tracking control approach is proposed for a class of continuous-time nonlinear systems using the goal representation HDP(GrHDP)with the f i lter-based action network.Notice that most previous researches about optimal tracking control focus on aff i ne systems and the reference signals are usually assumed to be differentiable.In[43],an ADP-based optimal control method with experience replay is proposed for underactuated snake robots.It is worth pointing out that one of the diff i culties in implementing ADP online for nonaff i ne nonlinear systems directly lies in the desired control input that can not be obtained directly using the f i rst-order necessary condition.Besides,a problem in tracking control with a nondifferentiable or discontinuous reference signal is that the error dynamics are hard to establish.Also,discontinuous reference signals(i.e.,step signal)could cause the sudden change of the control input,which is hard to implement on the mechanical actuators.According to the problems mentioned above,it is urging to design a new type of controller.

The parallel control,proposed by Wang[1],[2],[44]−[46],is a powerful method to solve many control problems based on the parallel system theory.The structure of the parallel system is shown in Fig.1.The main idea of parallel control is to expand practical problems into virtual space,and then to solve the control problems by virtual-reality interaction[1].Parallel control can also be referred to as the ACP methodology[1],[44],which is a trilogy:artif i cial systems(A),computational experiments(C),and parallel execution(P).

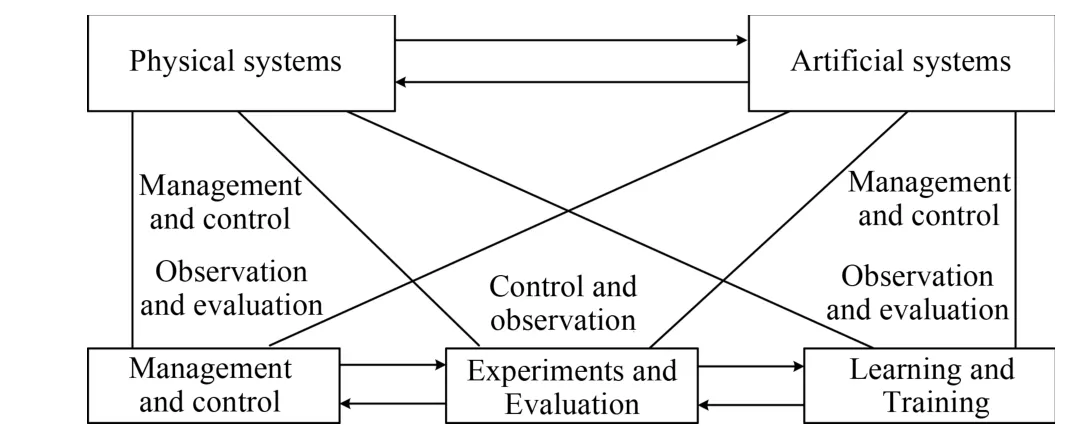
Fig.1.Structure of parallel system.

Fig.2 shows the parallel execution that is established based on the parallel system theory.Many processes,such as the experiment and evaluation,learning and training,management and control can be executed based on the interaction between the artif i cial systems and physical systems.Researchers have made considerable fruits on the parallel control and the parallel systems,such as intelligent transportation systems,intelligent vehicle systems,and computer vision,see e.g.,[2],[47]−[51]and references therein.However,the study of optimal parallel control for nonlinear systems is insuff i cient,which motivates our research.

This article studies the optimal tracking control for general nonlinear systems under the parallel control theory framework of the literatures[1],[2],[44]−[46].The parallel control theory is introduced into the nonlinear optimal control.The main contributions of this article are summarized as follows.

1)An augmented system and an augmented performance index function are proposed,and the general nonlinear system is transformed into an aff i ne system.It is proven that the optimal parallel control with the augmented performance index function can be seen as the suboptimal state feedback control with the traditional performance index function.

2)Based on the augmented system and the augmented performance index function,the ADP technique is employed to implement the optimal parallel control by using a critic NN to estimate the solution of the HJB equation.It is proven that the tracking error states and the NN weight errors are uniformly ultimately bounded(UUB).The continuity of the control signal can be guaranteed by the parallel controller with certain discontinuous reference signals,which is a good property in industrial applications.

The remainder of this paper is organized as follows.In Section II,a brief description of the parallel control is given and the problem of optimal parallel tracking control is formulated.In Section III,an augmented system is proposed with an augmented performance index function,and the difference between the optimal parallel control and the optimal state feedback control is analyzed theoretically.In Section IV,an ADP-based optimal parallel control is developed with the theoretical analysis.Simulation results are provided and discussed in Section V.Section VI gives some conclusions of this study.

II.PROBLEMFORMULATION

In this section,a brief description of the parallel control is given and the comparisons between the parallel control and state feedback control are shown.Then,the problem of the optimal parallel tracking control is presented.

A.Parallel Control

In this subsection,the parallel control is introduced brief l y.More detailed descriptions for parallel control can be found in[1],[2],[44]−[46],[52].Consider the following system

with statesx∈Rn,control inputu∈Rm,andh(x,u)∈Rn.The parallel control,which is shown in Fig.3,can be established.The parallel control is given by

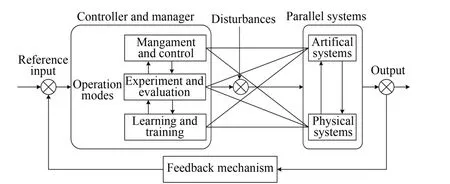
Fig.2.Structure of parallel execution.

Fig.3.Structure of parallel control.

Notice that the control input is introduced into the feedback system.Since control inputuis no longer generated passively by the statex,˙u=g(x,u)can be seen as an artif i cial system.

The dynamic system(1)and the dynamic parallel controller(2)are executed in parallel with information interaction.It is obvious that there exist the differences between traditional feedback control and parallel control.The state feedback control input is generated based on the state.

According to(1)and(2),we have

B.Optimal Parallel Tracking Control

According to the system(9),parallel control of the system(4)is different since control inputuis introduced into the feedback system,the energy function ofuis considered as a part of the Lyapunov function.So different from the Lyapunov functionV(e)for state feedback control,an augmented Lyapunov functionVp(e,ue)should be considered.The optimal state feedback control methods can not be used directly,i.e.,ADP and linear quadratic regulator(LQR).

The following assumptions are made for the system(4)for convenience of analysis.

Assumption 1:Assume that:

1)f(x,u)is Lipschitz continuous on a compact set Ωincluding the origin,system is stabilizable on the Ω,andf(0,0)=0.

2)Statexis measurable;

3)Reference signalxd(t)is a bounded piecewise smooth function with bounded derivatives and f i nite jump discontinuities.

Remark 1:The reference signals mentioned in Assumption 1 contain the most common signals,i.e.,step signal,square wave signal,sine signal.

III.OPTIMALPARALLELTRACKINGCONTROLDESIGN

In this section,the optimal parallel tracking control is developed.First,an augmented system and an augmented performance index function are proposed.Then,the difference between the optimal parallel control and optimal state feedback control is analyzed theoretically.

A.Augmented Error System

As mentioned above,the traditional optimal control methods can not be used directly due to the introduction of parallel controller(2).Inspired by[53],[54],a variable is introduced as follows:

B.Comparison With The Optimal State Feedback Control

Compared with the optimal state feedback control,a new symmetric positive def i nite matrixRpis introduced in performance index function to restrict the energy of˙ue.The difference between the optimal parallel control with differentRpand optimal state feedback control will be analyzed in the following.

Consider the system(6)and the performance index(7),the value function of an admissible controlue(e)is def i ned as

Remark 5:In the optimal state feedback control,researchers pay more attention to the quality and constraints of control inputuand show less attention to the quality of˙u.But it is not proper for many control problems,e.g.,160 MW Boiler-Turbine-Alternator Units[33]proposed by Astr¨om.The parallel control theory combines with the existing control methods can achieve better performance,e.g.,backstepping,LQR,and ADP.

IV.IMPLEMENTATIONWITHADAPTIVEDYNAMIC PROGRAMMING

A.Off l ine Implementation

HJB equation(37)can be solved off l ine based on the HDP with a classical three NNs framework that is suggested by Werbos[10],[11].The detailed training strategies of the iterative ADP can be found in[3],[22].

The difference with the existing work is that the developed method does not try to obtain the optimal controlu∗ewhich is acting on the real physical system,but to obtain the optimal derivative of the control˙u∗e.

Furthermore,it should be noted that HJB equation(37)can be solved without concrete equation of system(4)by using HDP,becausegsis an artif i cial one and is given by

Once iterativeVp(s)is obtained,the iterativevs(s)can be obtained using the f i rst-order necessary condition.

The diff i culty in solving HJB equation(37)without concrete equation of system(4)is to design feedforward controludandvd.When it comes to optimal regulator problem,ud=vd=0.Then,the problem mentioned above would not exist.

B.Online Implementation

To achieve online implementation,a critic NN is utilized to approximateV∗p(s)as follows:

The key advantage of the tuning rule(48)is that it does not require an initial admissible control input for(11)by introducing(50).Note that the tuning rule is different than that in[30]as it is designed to obtain the optimal derivative of control input.

The stability of system(4)with the parallel control(43)and tuning rule(48)is provided in the following.Before starting,the def i nition of UUB and Assumption 3 are given as follows.

Theorem 2:Consider the system(5)with the parallel control input(40)and tuning rule(48).Let Assumptions 1–3 be met.Then,the tracking erroreand the estimation error of the critic NN weights vector˜W=W∗−ˆWare UUB.The control inputuis continuous.

Proof:As motivated in[30]and[31],the detailed proof of Theorem 2 is given in the Appendix.

Remark 6:The virtual variableeuis introduced in constructing the augmented error system(11).It is worth pointing out thateu=u−ud,so no actual measurement is added when implementing the optimal parallel control.

Remark 7:Generally speaking,the stability of the system(1)can be guaranteed theoretically in optimal state feedback control with jump discontinuities,but it requires control inputuis able to make the step-changes at the jump discontinuities,which is diff i cult to execute on the mechanical actuators.

V.NUMERICALANALYSIS

In this section,two simulations are employed to evaluate the effectiveness of the developed optimal parallel control.

Example 1:In the f i rst example,we consider the following linear system[56]

where optimal gain matrixK=£0.2361 6.2361⁄.

The initial statex(0)=[0,0]T.The initial control inputeu(0)=ue(0)=0.2361.The trajectories of the system state are shown in Fig.4,and the trajectories of the control input are shown in Fig.5.It can be seen from the Figs.4 and 5 that the system is stable with the parallel controller,and statexis able to trackxdsteadily.

Fig.4.State trajectories of Example 1.

Fig.5.Control input of Example 1.

Furthermore,it can be seen from the Figs.4 and 5 that within the f i rst four seconds,the optimal parallel controller is capable of achieving almost the same performance with the optimal state feedback controller.Performance index(7)

Vvs(e(0))=13.2367 andVue(e(0))=13.2361.

With the sudden change of the reference signalxdin the fourth second,the overall control inputuof the optimal state feedback controller abruptly changes at this point as the steady-state controllerudsteps from 2 to 4 and error statee1steps from 0 to 1,which is diff i cult to achieve on actuators.Compared with the optimal state feedback controller,the optimal parallel controller provides a more reasonable way by introducing the control input into feedback.The control input of the optimal parallel controller is continuous even with the sudden change of the reference signal.In engineering applications,it is important to choose a reasonableRpaccording to the practical restrictions of mechanical actuators.

To compare the difference between the optimal state feedback controller and parallel controller with differentRp,the relative difference(RD)is def i ned as:

whereNis the length ofuvandu,anduv=eu+ud.

The RD with differentRpis shown in Fig.6.It can be seen from Fig.6 that the difference betweenueandeuis decreasing as theRpdecreases.The optimal parallel controller withRp≤10−5behaves pretty much the same as the state feedback controller as Corollary 1 predicted.So different performance can be achieved by choosingRpaccording to the control objectives and the practical restrictions.

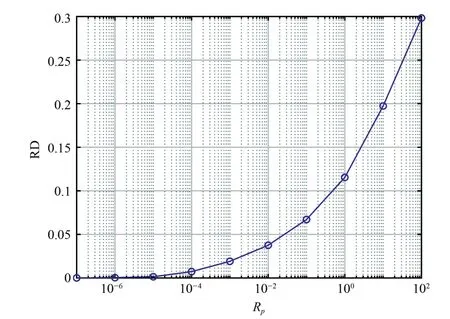
Fig.6.RD with different Rp.

Fig.7.State trajectories of Example 1 with time-varying reference signal.

Example 2:In the second example,we examine the performance of the developed optimal parallel controller in a nonaff i ne system:

Fig.8.Control input of Example 1 with time-varying reference signal.

Qpis chosen to beI3×3andRpis chosen to be 1.The initial state isx(0)=£1−1⁄T,initial control inputu(0)=1.7647,and the initial critic NN weighs are chosen to be 0.The parameter of tuning ruleα1=10 andα2=1.The trajectory of the system state is shown in Fig.9,the trajectory of the control input is shown in Fig.10,and the trajectories of the critic NN weights are shown in Fig.11.It can be seen from Figs.9–11 that the developed optimal parallel tracking controller is able to stabilize nonlinear system effectively,the tracking error converges to zero or a small neighborhood of zero.

Fig.9.State trajectories of Example 2.

Fig.10. Control input of Example 2.

Fig.11. Critic NN weighs.

Furthermore,it can be seen from Figs.9 and 11 that the critic NN weighs converge as the tracking error converges to zero.The performance with the f i nal critic NN weighs is better than with the initial critic NN weighs.In parallel control,control input is seen as a state,so the control input of the optimal parallel controller is continuous with the sudden change of the reference signal as predicted.This property is very useful in industrial applications,especially for the control of the switched systems,as long as the candidate Lyapunov function for system is radially unbounded,the system will be stable with any initial control inputu0.

VI.CONCLUSION

Optimal parallel tracking control for general nonlinear systems via ADP is studied in this research.Different from the optimal state feedback controller,the variation of the control of the optimal parallel controller is constructed based on both system state and control input.First,an augmented system and an augmented performance index function are proposed.Then,it is proven that the optimal parallel control with the augmented performance index function can be seen as the suboptimal state feedback control with the traditional performance index function.Moreover,the ADP method is utilized to implement the optimal parallel control without using value iteration or policy iteration.We prove that the tracking error state and the NN weights error are UUB and control input is continuous with the optimal parallel controller.Finally,the effectiveness of the developed optimal parallel control method is verif i ed in two cases.

APPENDIXA PROOF OFTHEOREM2

Therefore,statesand the critic NN weights error vector˜Ware UUB.

Note thatud,which is constructed based on thexd,is a feedforward control input andxdis a bounded function with bounded derivatives.Therefore,udis UUB.Moreover,eTe≤sTs,which meanseis UUB.

Jump discontinuities of thexdlead to the sudden change of states,which means tuning rule(48)could be activated.As the tuning rule(48)guarantees the stability of(11)with any initial critic NN weights vectorˆWand jump discontinuities are f i nite,the signalse,and˜Ware UUB.

Finite jump discontinuities of thexdlead to the f i nite jump discontinuities or removing discontinuities ofvsand˙ud.According to(5),(10),and(11),we have

Thus,the global continuity ofucan be guaranteed. ¥