Stabilization Parametric Region of Distributed PID Controllers for General First-Order Multi-Agent SystemsW ith Time Delay

Xinyi Yu,Fan Yang,Chao Zou,and Linlin Ou

Abstract—The stabilization problem of distributed proportional-integral-derivative(PID)controllers for general first-order multi-agent systems w ith time delay is investigated in the paper.The closed-loop multi-input multi-output(M IMO) framework in frequency domain is firstly introduced for themulti-agent system.Based on thematrix theory, the whole system is decoupled into several subsystems w ith respect to the eigenvalues of the Laplacian matrix.Considering that the eigenvalues may be complex numbers, the consensus problem of the multi-agent system is transformed into the stabilizing problem of all the subsystems w ith complex coefficients. For each subsystem w ith complex coefficients, the range of adm issible proportionalgains is analytically determ ined. Then, the stabilizing region in the space of integral gain and derivative gain for a given proportional gain value isalso obtained in an analytical form. The entire stabilizing set can be determ ined by sweeping proportional gain in the allowable range. The proposed method is conducted for general first-order multi-agent systems under arbitrary topology including undirected and directed graph topology. Besides, the results in the paper provide the basis for the design of distributed PID controllers satisfying different performance criteria.The simulation examples are presented to check the validity of the proposed control strategy.

I.In t roduction

IN recent years,the distributed cooperative controlof multiagent systems has attracted extensive attention due to their w ide applications inmany areas such as formation control[1],distributed computing[2]and sensor networks[3].One critical issue arising from multi-agent systems is to design distributed control protocols based on local information that enable all agents to reach an agreement on certain quantities of interest, which is known as the consensusproblem.

So far,increasing results of consensus problems formultiagent systems have been obtained.In[4],the consensus problem of first-order integrator multi-agent system was discussed originally.The dynamical consensus algorithm for the second-order multi-agent system was proposed in[5],where all agents achieved the same dynamical value.Sampled-data consensus of the second-order multi-agent systems w ith time delay was investigated in[6].The necessary and sufficient conditions for consensus in third ordermulti-agent systems were obtained in[7].In addition,otherwork about the distributed consensus problem formultiagent systemsw ith different dynam icscan be seen in [8]–[11].In real applications, the agents are generally described by first-order dynam ic model.In[12],the model predictive control scheme was applied for multi-agent systems w ith discrete-time single-integrator dynam ics under sw itching directed interaction graphs.The cluster lag consensus for multi-agent systems w ith a time-varying communication topology and heterogeneous multi-agent systems w ith a directed topology was studied in[13].Hence,the consensus problem of first-order multi-agent systems is very important.It was concluded that the condition for the single-integrator system to achieve consensus was that the network communication topology has a spanning tree.However,such the condition may not ensure the general first-order multiagent systems to reach consensus.

In addition,in practical applications, time delays often appear when local information data travel along in a largescalenetwork.Delay effect isan important issueon consensus problemssince it may affect the control performanceand even its stability[14].Therefore,it is desirable to design the distributed control protocol for the general first-ordermultiagent systems w ith time delay.Up to date,some literatures have been presented to design distributed control protocols for multi-agent systemsw ith time delay in time domain.In[15],the consensus protocol based on the low gain solution of a parametric algebraic Riccati equation was designed for the multi-agent systemsw ith time-varying communication delay.The effect of quantized dwell times in solving consensus problems in time-delayed multi-agent systems was investigated in[16].In[17],a predictive tracking controller is proposed to compensate the negative effects caused by bilateral time-delays in a w ireless network.Recently,some researches have been devoted to multi-agent systems w ith time delay in frequency domain.The frequency domain method is proved to be effective for the time-delay issue because the time delay is a non-minimum phase term whose amplitude isalwaysequal to 1.In[18],an analyticalapproach to designcontroller of multi-agent systems w ith time delays was presented.In[19],thedisturbance rejection controller was proposed for synchronized output rejection of multi-agent systems w ith time delay.The above-mentioned consensus protocols are effective for small-scale multi-agent systems w ith time delay.When the number of the agents increases, thesemethods become complicated.Besides, these methods cannot be utilized to design multi-agent systems under directed topology graph since the Laplacianmatrix has complex eigenvalues.For multi-agent systemsw ith time delay under directed topology,the design of the distributed controllers isstill challenging.Due to the advantages of the proportional-integraldifferential(PID)controllers in control engineering and application,it is desirable to introduce the distributed PID controller into the multi-agent system to improve the consensus performance.A distributed PID protocol was designed for the consensus of homogeneous and heterogeneous networks using appropriate state transformations and Lyapunov functions[20].In[21], thePID feedback for arbitrary-order delayed multi-agent systems was investigated.In the actual engineering application,the distributed PID controllers are generally required to meet several performance criteria simultaneously.To reach this purpose,a natural idea is to first present the stabilizing regions of the distributed PID controllers and then design the PID controller by finding the intersection of the controlparameters meeting each required criterion.Thus, the problem of determ ining the stabilizing PID region is important from a practical viewpoint.Some effective approaches on presenting the stabilizing region of the PID controller have been reported for linear systems w ith time delay[22],[23].To the best of the authors’know ledge,there are few literatureson presenting the stabilizing region of the distributed PID controllers for multi-agent systems under directed topology.

Motivated by the above-mentioned discussion,the stabilizing region of the distributed PID controllers is derived for the general first-order multi-agentsystems w ith time delay under fixed topology.Firstly,a multi-input multi-output(M IMO)framework is introduced to uniform ly describe the multi-agent systems w ith time delay in frequency domain.Then based on thematrix theory and graph theory,themultiagent system is decoupled into several subsystems w ith respect to the eigenvalues of the Laplacian matrix.Since the eigenvaluesmay be complex numbers,the consensus problem of the multi-agent systems is transferred into the stabilizing problem of the subsystems w ith complex coefficients.For each subsystem,the range of admissible proportional gains()is analytically determined.Then,the stabilizing region w ith respect to the integral gain()and derivative gain()for a givenvalue in the range can be also obtained in an analytical form.By computing the intersection of the resultant regions for all the subsystems,the stabilizing (,)region of the distributed PID controller is derived.The entire set can be determ ined by sweepingin the allowable range.The parameters chosen in the resultant set can guarantee the consensus of the multi-agent system w ith time delay.The proposed method is conducted for general first-order multiagent systems w ith time delay under arbitrary topology,including undirected and directed topologies.Further,the results in the paper solve the stabilization problem of the systems w ith complex coefficients and provide the basis for the design of distributed PID controllers satisfying different performance criteria.

The paper is organized as follows.In Section II,some basic concepts about the graph theory and the stabilization for the systems w ith time delay are introduced.The problem statement and the design objectiveare presented in Section III.The approach for determining the stabilizing setof distributed PID controllers is proposed in Section IV. Numerical examples are provided to demonstrate the validity of the main results in Section V.Finally,the conclusion is given in Section VI.

II.Prel imina r ies

In this section,some basic concepts about the graph theory and the stabilization of time-delayed systemsare introduced.

A.Graph Theory

B.Stabilization of the System With Time Delay

Many problems in control engineering involve time delays.These time delays lead to dynam ic modelsw ith characteristic equationsof the form

III.Problem Sta temen t

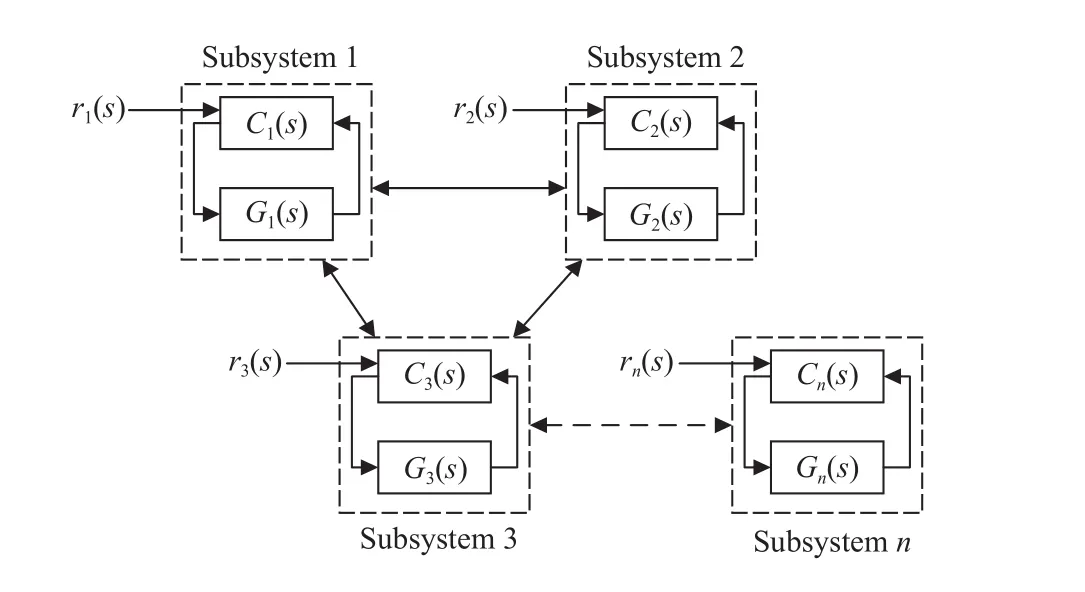
Fig.1.The control block diagram for the subsystem.

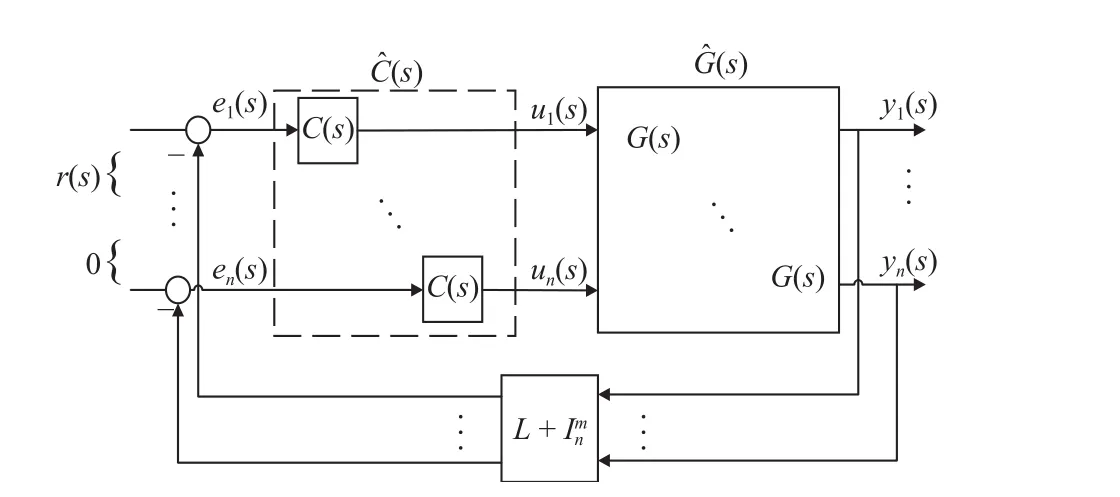
Fig.2.TheM IMO model of themulti-agent system.

For the known agent dynam ics and the fixed communication topology,the objective of the paper is to obtain the complete stabilizing set of the distributed PID controllers analytically for general first-order multi-agent systems.

IV.Stabil iza tion Ana lysisof Dist r ibuted PID Cont rol lers

From(8),it can be derived that the characteristic equation of themulti-agent systems is

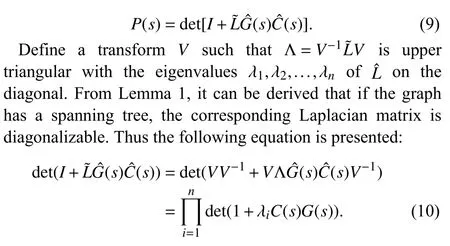
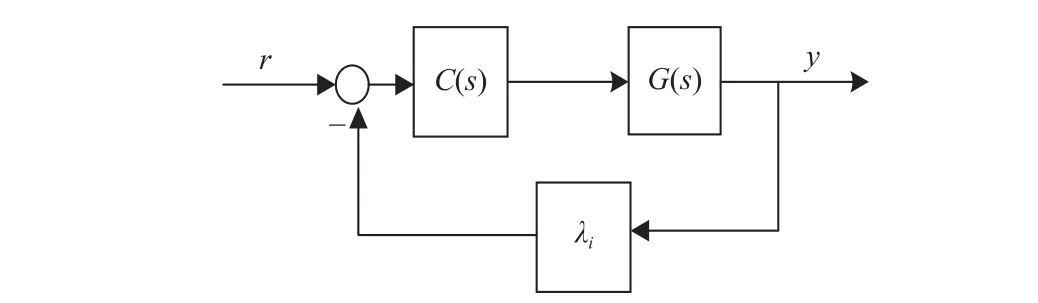
Fig.3.The control block diagram for the subsystem.

A. Determination of Admissible Range

Assume that theeigenvaluesof the Laplacian matrix is

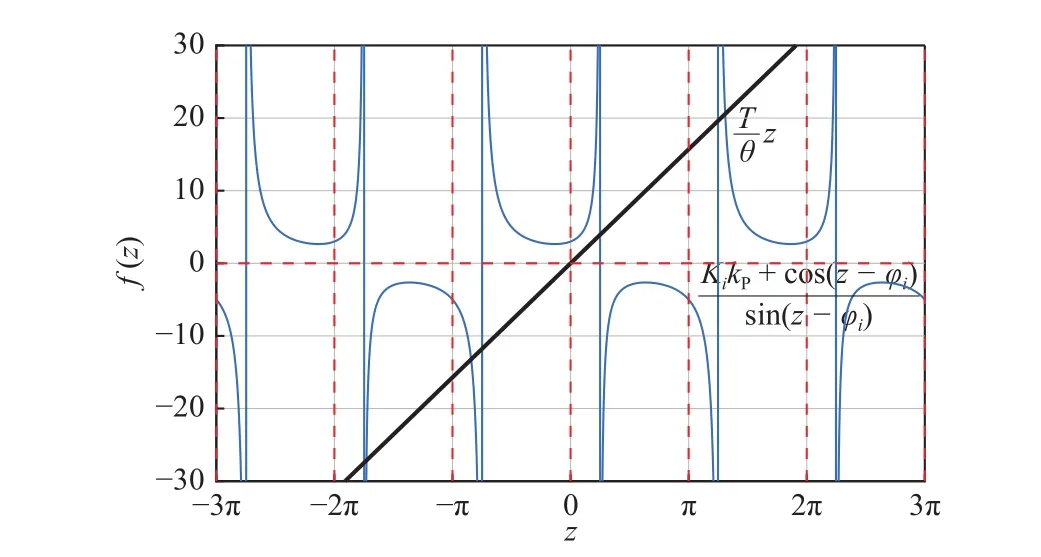
Fig.4.Plotsof terms involved in (27)for .

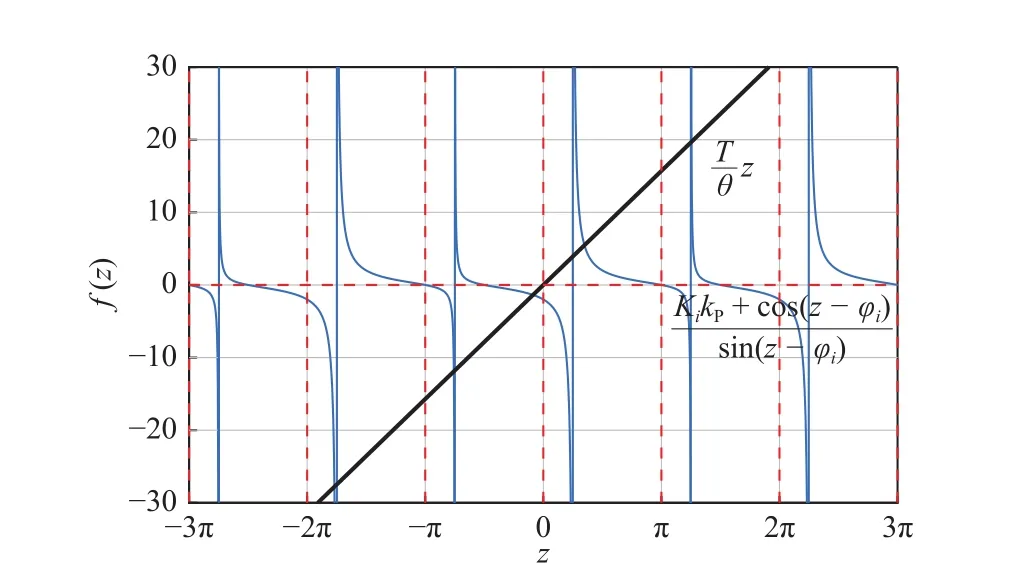
Fig.5.Plots of terms involved in (27)for .

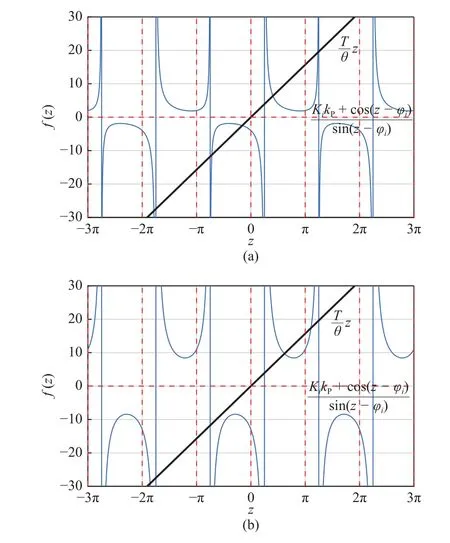
Fig.6.Plots of terms involved in(27)for.(a);(b).

B. Determination of the Stabilizing Set for the Distributed PID Controllers

C. Algorithm for Determining Stabilizing PID Parameters

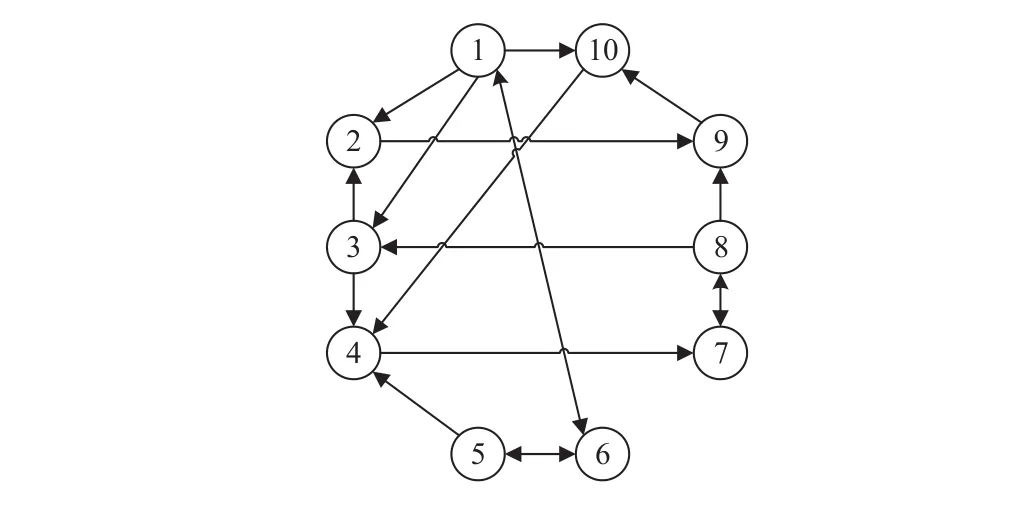
Fig.7.The direct topology for Example 1.

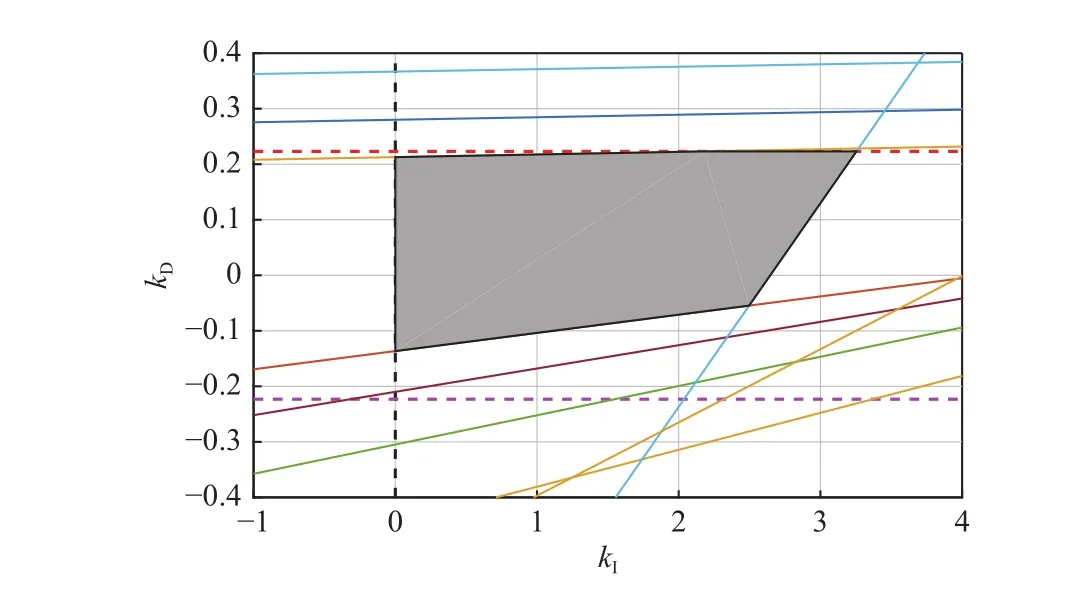
Fig.8.The stabilizing region for .

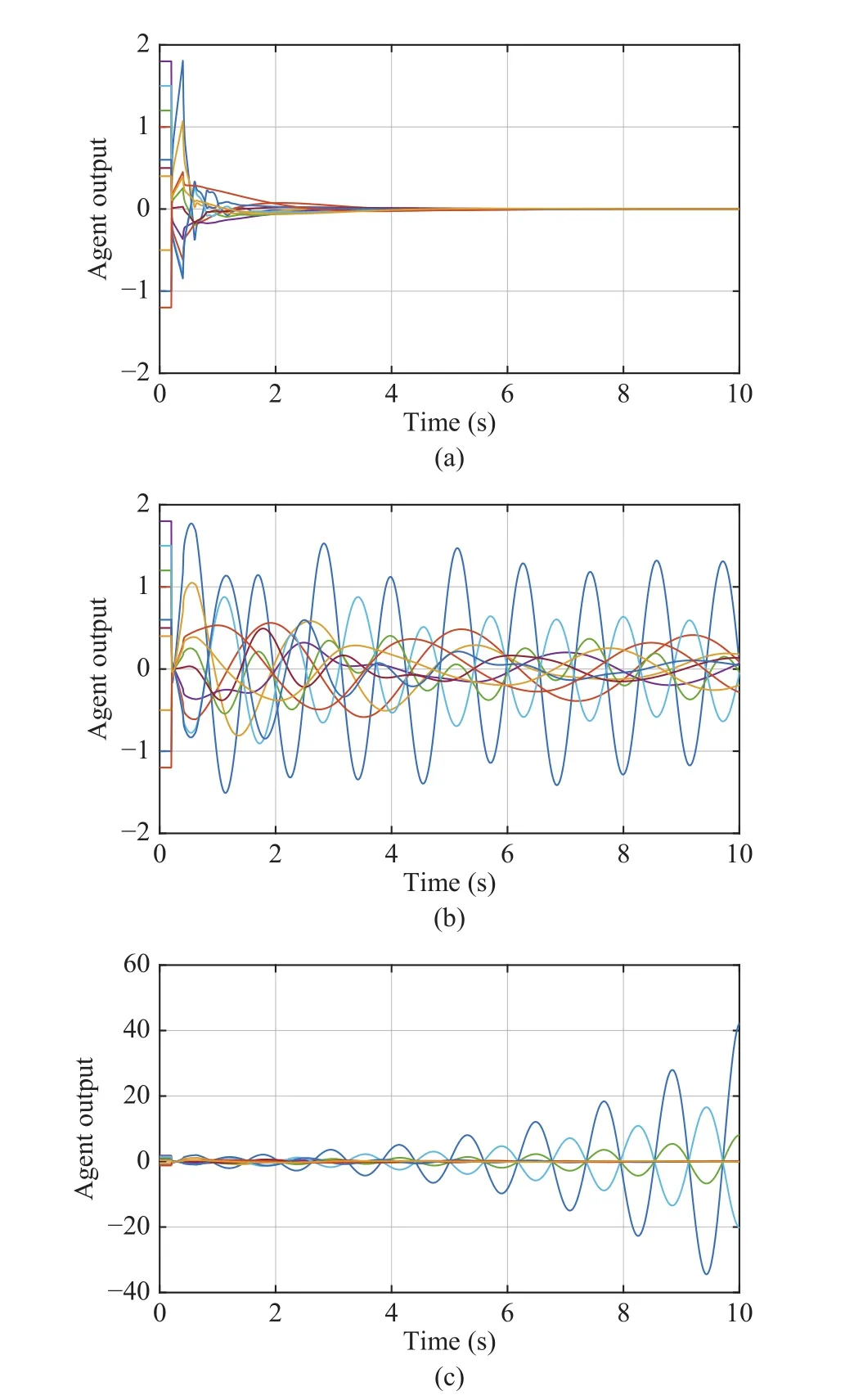
Fig.9.The output response for :(a);(b);(c).

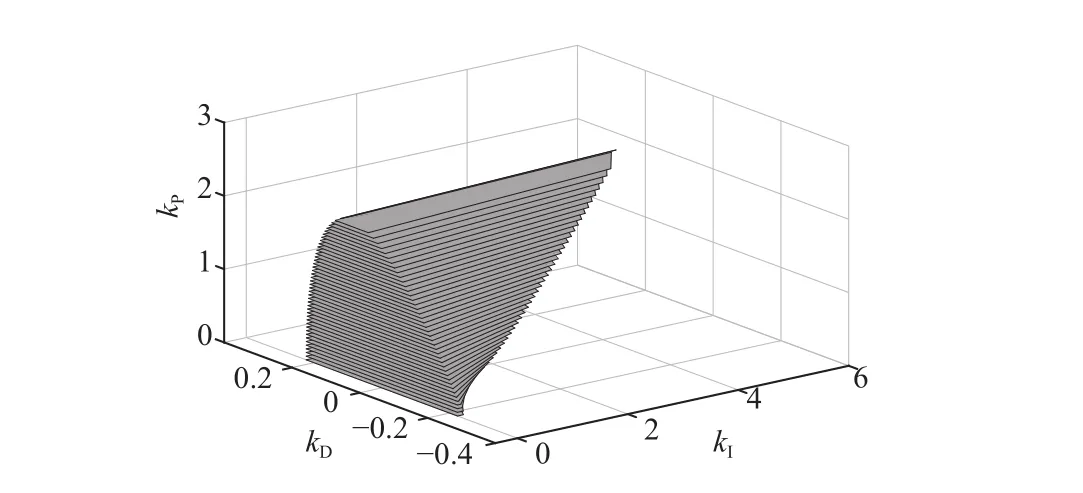
Fig.10.The stabilizing parametric region for the multi-agent systems.

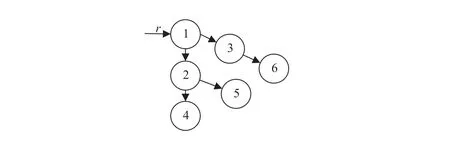
Fig.11.The direct topology for Example2.

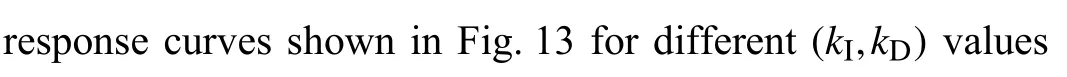
Fig.12.The stabilizing region for .

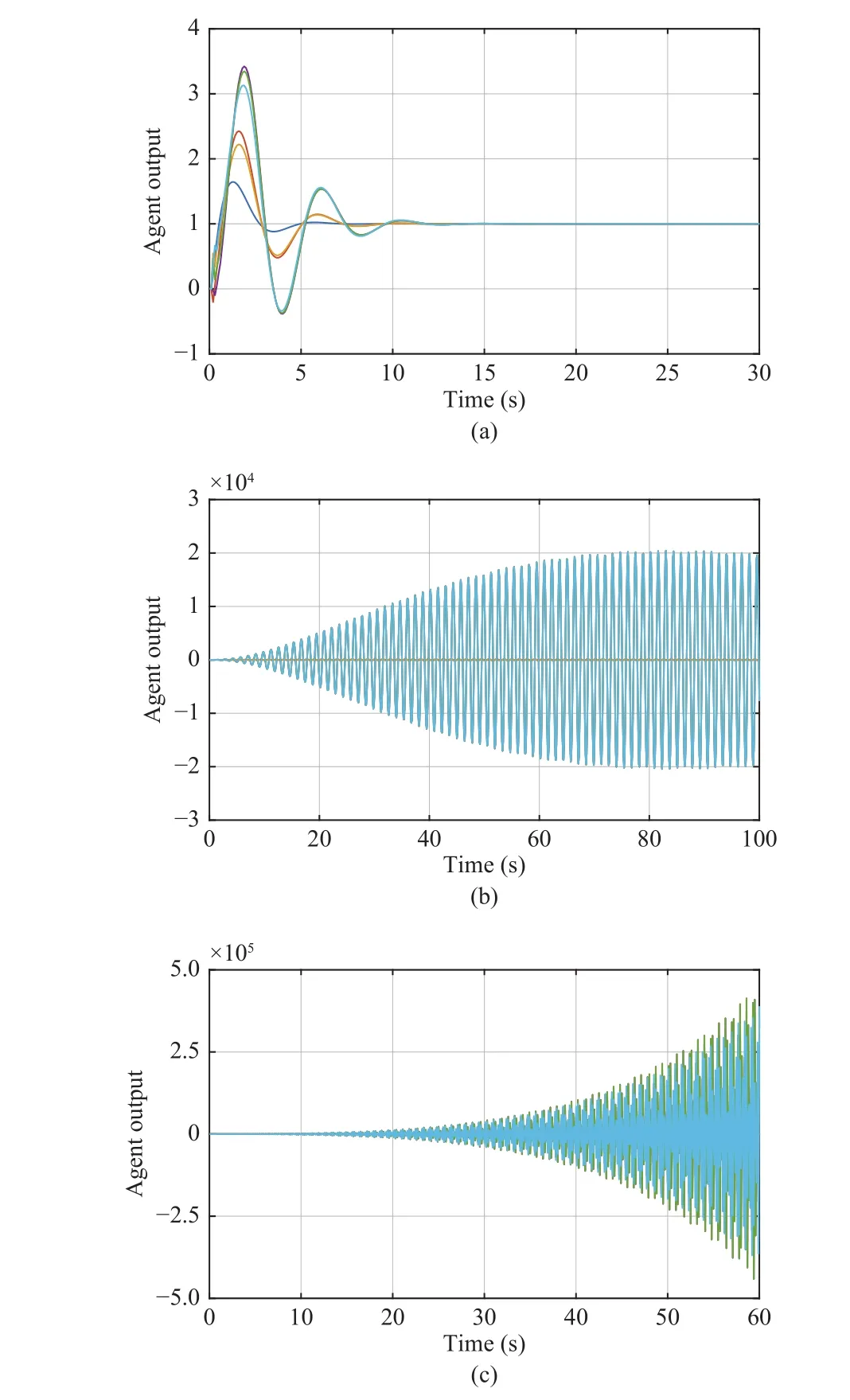
Fig.13.The output response for :(a);(b);(c) .

VI.Conc lusion

A comprehensive method to compute the entire set of stabilizing distributed PID controllers for general first-order multi-agent systems under arbitrary fixed topology is presented in this paper.A ll the parameters chosen in the resultantstabilizing region can guarantee the consensusof the given multi-agent system.The results of the paper provide insight into designing and analysing of the distributed PID controller for general first-order multi-agent systems under fixed topology including the undirected and directed topology.Further,the results in the paper solve the stabilization problem of the systems w ith complex coefficients.