“还原法”巧解小学数学应用题

2020-11-05江苏省苏州工业园区第三实验小学吴陈轶

天津教育 2020年30期

■江苏省苏州工业园区第三实验小学吴陈轶

数学习题的解答过程中，一般是根据已有的条件进行思考与分析，从中找出解决的方式。我们可以运用一些已知的条件，反向推导，解决这类的数学题型，这种方式被称之为“还原法”，也称之为“倒推法”。

一、从“单个对象”着手，按部就班

“单个对象”主要是指在习题中，只有一个主语与总量，并且在解题过程中，即使条件发生变化，但是最后所求解的结论依然是主语与总量。

如，超市售卖一批香蕉，第一天卖掉了总体香蕉的1/2，第二天卖掉剩下的1/2并多售卖出10千克，然后第三天卖掉第二天剩下的1/2并少3千克，这些苹果最后还剩下10千克，请问这一批香蕉一共有多少千克？在这一道习题里面，“一批香蕉”是其中的主语，也是这道习题中的“单个对象”，因此不管这一批香蕉经历几天的贩卖，都需要解答“一批香蕉”是多少千克。在面对这样的习题中，为方便理解，一般都需要建立流程图、还原图或者倒退图，对这三种图像中的一种进行分析。这三种方法的选用中，需要根据班级学生的数学水平，确切地选择方式，以下将论述其中的一种方式。

所运用的方法为流程图方法。首先，需要做出其中的流程图，即图1。流程图的绘画较为简单，只需要根据习题内容进行绘画，如，将每天店中剩下的香蕉用空格表示，并在箭头上标注好每天售卖的量，流程图的绘画就完成了。计算也较简单，只需要向前推导即可，但是要注意在推导过程中变化符号。在流程图的绘画中，学生大多会发生以下两种错误。第一，对于在绘画箭头上的标注中，对于“多卖出10千克”“少2千克”的符号运用出现错误，这是就需要他们对于习题与流程图中各种知识点都有明确的认知，明白空格是店内所剩的香蕉质量，从而理解所需什么符号。第二就是计算中所出现的错误，在进行计算时，是需要进行反向计算，因此在计算时，需要对符号进行修改，如，箭头上的减法，计算时需要修改成加法等。或者在计算时，对于计算的顺序发生错误，在进行反向计算时需要反向推导，因此在列式时需要添加一定的括号，防止计算顺序的错误，对其进行计算有所帮助。

图1流程图

二、从“多个对象”出发，灵活运用

“多个对象”其中主要是指：在习题中，会有多个主语在其中，并且在计算过程中，多个主语也会同时出现变化，但是在最后所求得的依然会是这些多个主语或者这些多个主语的部分。例如，在三辆公交车上，有48个人乘坐前往同一个地方，但是每辆车上的人数不等，因为部分原因需要平衡人数，因此从第一辆车中下来6人到第二辆车中，之后在第二辆车中下来8人到第三辆车中，从而车中人数平衡了，请问原来三辆车中分别有多少人？

在这道习题中，主要有三个主语对象，即在刚开始时三辆车上的人数，在习题中这三辆车上的人数都在发生变化，最后达到一致的数目。因此，在学生初次接触这类习题中，都难以直接进行解决，主要是因为在其中涉及多个主语，并且其中的数量还在不断变化，这就需要教师进行一定的引导。对于上一习题主要可以绘画出以下的示意图，如图2。

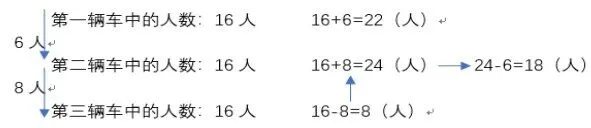
图2车辆中人员的调动

通过图2，不难发现在最后每辆车中的人数相同，因此最后每辆车中都会有16人，因此，一次推导，通过“之后在第二辆车中下来8人到第三辆车中”这句话可以推导出，在这次人员调动之前，第三辆车只有8人，第二辆车有24人。最后，再根据“因此从第一辆车中下来6人到第二辆车中”这句话得出，最开始第一辆车有22人，第二辆车有18人。通过逐次推导的方式得出结论，在这种类型题的解决中，学生主要需要注意两点，首先，在建立示意图后，直接根据数量关系和习题中的话语，反向推导。最后就是需要注意其中的数量关系，注意其中的各种符号运用。

三、以“不同对象”分析，确定核心

“不同对象”同样是指多个主语，但是“不同对象”的多个主语与“多个对象”的多个主语不同，“多个对象”的多个主语一般是指同种的事物，而“不同对象”的多个主语是指不同的事物，并通过反向推导的方式推导出“不同对象”的答案。例如，在商场引进一批香蕉进行售卖，最开始进行称重，香蕉与筐一共重104斤，通过一天的努力，上午售卖出一半的香蕉，下午也售卖出了上午所剩下的一半，最后再进行称重，香蕉和筐一共重29斤，问香蕉多重？筐多重？在学生进行分析中，如果未注意，就会根据“多个对象”的习题方法进行解答，但是在这道习题中，需要注意筐与香蕉是不同性质的物质，并且筐的质量一直未发生变化，香蕉的质量发生了变化，所以解答的方法就不同。介绍一种解答方式，如下：将其中的香蕉设置成一个未知数，先求解香蕉的质量，首先因为“最开始进行称重，香蕉与筐子一共重104斤”与“最后在进行称重，香蕉和筐一共重29斤”两句话，推导出一天一共售卖出了75斤，并且通过“上午售卖出一半的香蕉，下午也售卖出了上午所剩下的一半”可以看出售卖的75斤也是香蕉总量的3/4，通过计算得出香蕉的质量为100斤，再计算一下得出筐的质量为4斤。在这道习题的解决方式运用的主要为份数与比例法进行还原计算，在数学学习中所经常使用的方式。

四、让“相同对象”一致，加深印象

“相同对象”的特质与“单个对象”一致，在题干中主语以及总量相同，其所求的未知量与主语一致。例如：某水果店购入一批水果，第一天卖出的水果量比总量的一半少10斤，第二天卖出的水果比剩下的水果的一半多8斤，现在的水果量为20斤，问：这家水果店原本购入多少斤水果？从题干看，主语是这批水果，所求也是水果总量。针对此类题目，我们可以让学生先算出水果店原本购入的水果量［（20+8）×2-10］×2=92斤。当算出水果总量后，要学生进行检验，即用“还原法”进行反推：（92÷2+10）÷2-8=20斤。我们利用“逆向思维”进行推导检验，一方面可以检验此题正确与否，另一方面还能加深学生运用还原法检验此类题目的效果，提升了学生的解题效率。