基于BP神经网络的单管通信塔损伤识别研究

2020-11-05王清华荆建中陈振唐明波

特种结构 2020年5期

王清华荆建中陈振唐明波

(中讯邮电咨询设计院有限公司北京100048)

引言

20世纪90年代起至今，通信技术有了飞速发展，网络信号的覆盖要求不断提高，而铁塔作为搭载通信设备的重要结构，其建设量也有了突飞猛进的增长，目前全国在役的通信铁塔约200万座。随着5G建设步伐的加快，通信铁塔结构承受了更多的荷载。存量塔的共享改造次数逐渐升高，许多铁塔超负荷甚至带缺陷服役，导致在役铁塔存在很多安全隐患。

近年来，铁塔检测逐渐受到国内业界的关注，一些无损检测技术[1-4]与数值仿真技术[5-8]逐渐兴起。目前的铁塔检测技术大多为外观检测，属于静态检测的范畴，这些检测难以发现铁塔结构的微小损伤。基于BP神经网络的铁塔损伤识别技术[9-11]从铁塔结构的动力学参数变化来判别铁塔的损伤，可以克服传统检测技术的缺点。本文将该技术应用于铁塔结构的损伤检测中，拟得到铁塔刚度折减与自振频率之间的规律，并建立可靠的损伤评价指标与BP神经网络，以高效、准确的输出损伤判定结果。

1 铁塔损伤识别基本原理

通信铁塔结构常见的安全隐患为地脚螺栓锈蚀、塔底法兰处螺栓松动、缺失或安装不合理、塔身局部焊缝开裂、塔体防腐涂层脱落锈蚀等，这些损伤均会引起铁塔结构局部刚度减小或者铁塔截面减小，进而其自振频率会发生改变。因此通过分析铁塔结构的刚度折减可以获知结构的损伤情况，由结构动力学可知，多自由度结构体系的运动模型如图1所示，其运动方程为:

式中:[M]为质量矩阵；{C}为阻尼矩阵；[K]为刚度矩阵；{F(t)}为外部荷载量；{u}为位移向量。

图1 多自由度体系振动模型Fig.1 Multi-degree-of-freedom system vibration model

当无阻尼结构的作用力为零时，得到结构的自由振动方程:

求解得到特征方程为:

式中:{Φ}为位移矩阵；ω为自振频率。

结构局部损伤后刚度折减必定会引起刚度矩阵的折减，假设刚度矩阵变化量为[ΔK]，刚度折减后频率变为ω′，振型变为{Φ′}，质量矩阵损伤前后变化量很小，假定质量矩阵不变，则式(3)变为:

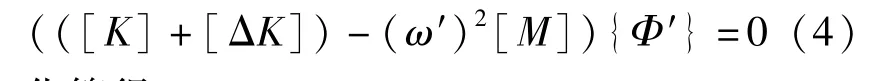
化简得:

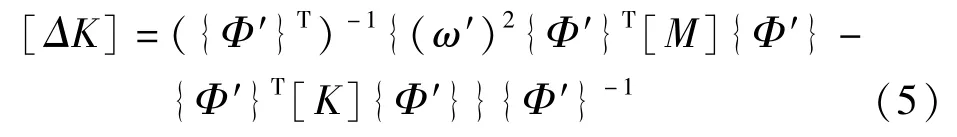
由式(5)可知，铁塔结构损伤前后刚度矩阵的变化与其振型、频率与损伤前的刚度矩阵有关，对于一个通信铁塔结构来说，其损伤前的刚度矩阵是确定的。因此，可以通过计算损伤后结构的振型及频率来识别出结构的刚度矩阵的变化，也就是识别出通信铁塔结构的损伤。

2 模态频率和位移计算

2.1 完整铁塔结构

单管通信塔由于其结构形式简单、造型美观等优点而被广泛应用，因此选取《通信铁塔标准图集V1.3》中40m单管塔(DGT(Z)-40-0.35-4ZJ)作为研究对象，单管通信塔立面如图2所示。

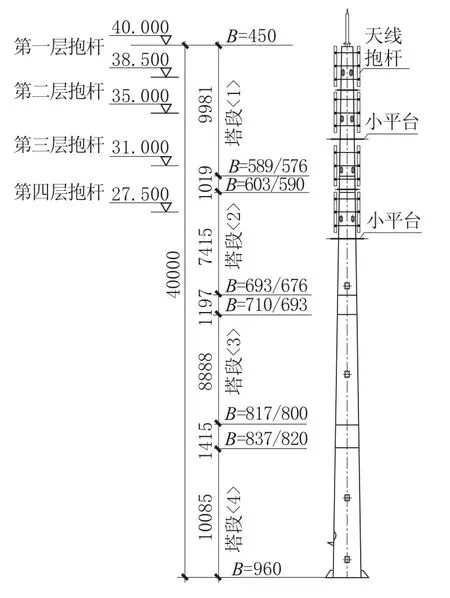
图2 40m单管通信塔Fig.2 Structure drawing of the 40-meter Single-tower

采用有限元软件ANSYS进行结构分析，选择SOLID45六面体单元模拟单管通信铁塔结构，此单元常用于构造三维实体单元，能更准确地反映出铁塔结构的真实状态，计算时假定单管通信塔材质均匀，无损伤，通信单管塔结构的材质见表1，铁塔模型如图3所示。

表1 无损钢材的材料特性Tab.1 Material properties of non-destructive steel

图3 铁塔模型Fig.3 Structure model of tower

为了验证ANSYS软件计算结果，另选择空间计算软件3D3S(V13)对单管通信塔进行建模并计算前三阶频率，两种计算软件的计算结果见表2。

表2 ANSYS模态分析和3D3S计算结果(单位：Hz)Tab.2 The analysis results of ANSYS and 3D3S(unit:Hz)

由表2计算结果可知，利用两种有限元分析软件得到通信塔的前三阶频率基本吻合。

2.2 损伤铁塔结构

为了能够更加真实地反映通信单管塔的实际损伤状况，利用有限元软件ANSYS软件将通信塔结构划分为10个单位，每个单元综合考虑两处损伤(每个单元均分为两段，从下至上依次为编号1、2)，损伤位置刚度分别折减10%、20%、30%。为了方便描述，对每种工况进行编号，其中损伤10%、20%、30%分别为CaseA、CaseB、CaseC，健康状态下为CaseH，如:CaseA01-2表示1单元的第2段损伤10%工况。图4为单管通信塔CaseH工况下的前三阶振型，表3为部分工况下的自振频率。

图4 单管通信塔结构前三阶模态振型Fig.4 Single-tower structure with first three modes

由表3计算结果可知，随着损伤位置和损伤程度的改变，结构的自振频率发生变化，这就证明了结构自振频率与结构的刚度矩阵相关，可作为结构损伤识别的指标，但由于频率为结构的整体性指标，不同损伤位置和损伤工况的结构可能会具有相同的自振频率，如:CaseA09-2工况和CaseC10-1工况的一阶频率相同，因此仅将频率作为通信铁塔结构的损伤识别的指标可能会出现误判的情况。

结构的振型是指弹性体或弹性系统自身固有的振动形式，可用质点在振动时相对位置即振动曲线来描述，选取结构的前三阶模态位移作为损伤识别的指标，计算不同损伤工况下模态振型，每种工况沿高度均匀取20个点的模态位移来表示铁塔结构的模态振型，由于篇幅限制，只列出部分工况下各模态位移，见表4。

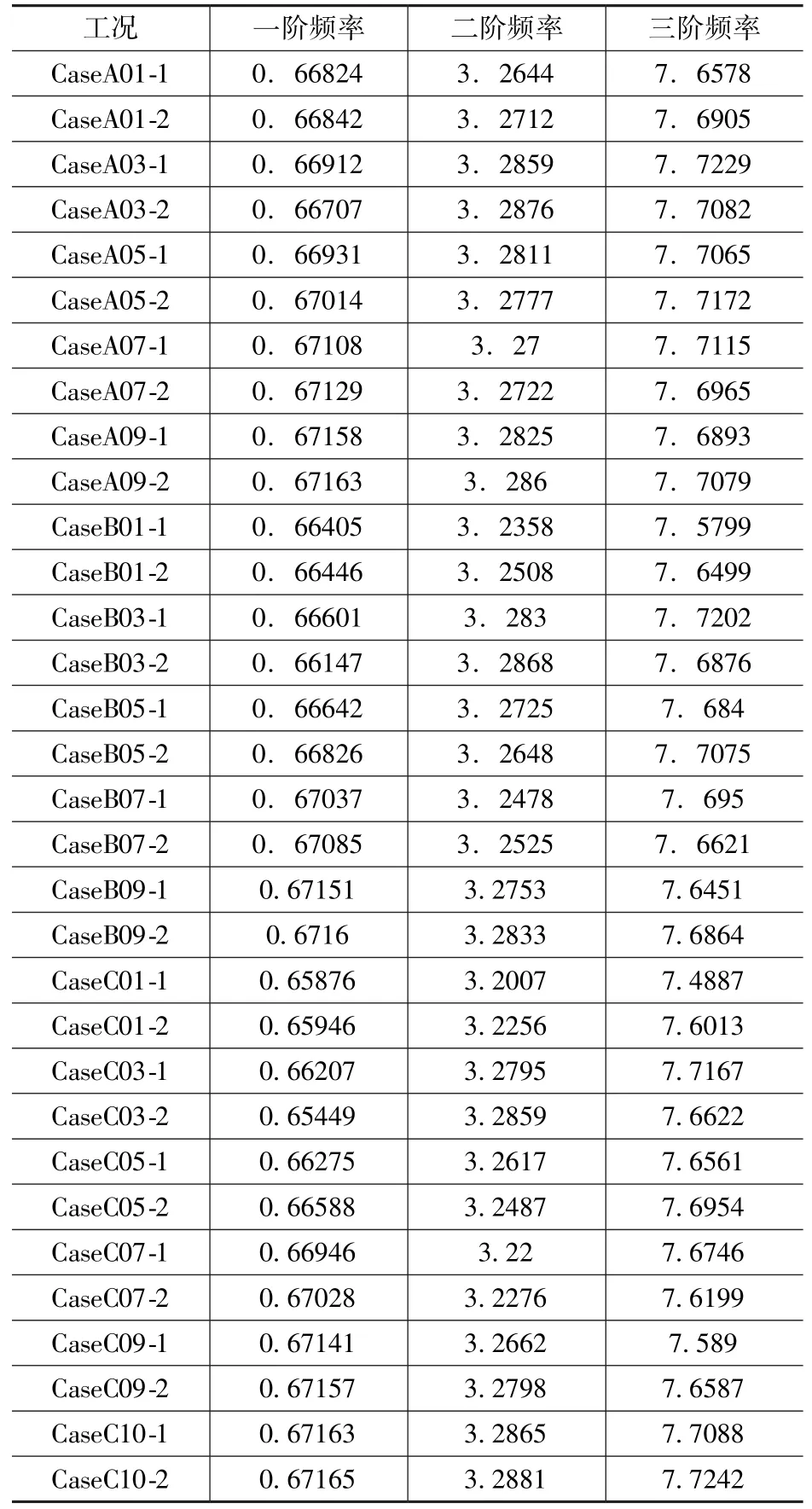
表3 部分工况下结构自振频率(单位：Hz)Tab.3 Free vibration frequency of each unit(Partial)(unit:Hz)

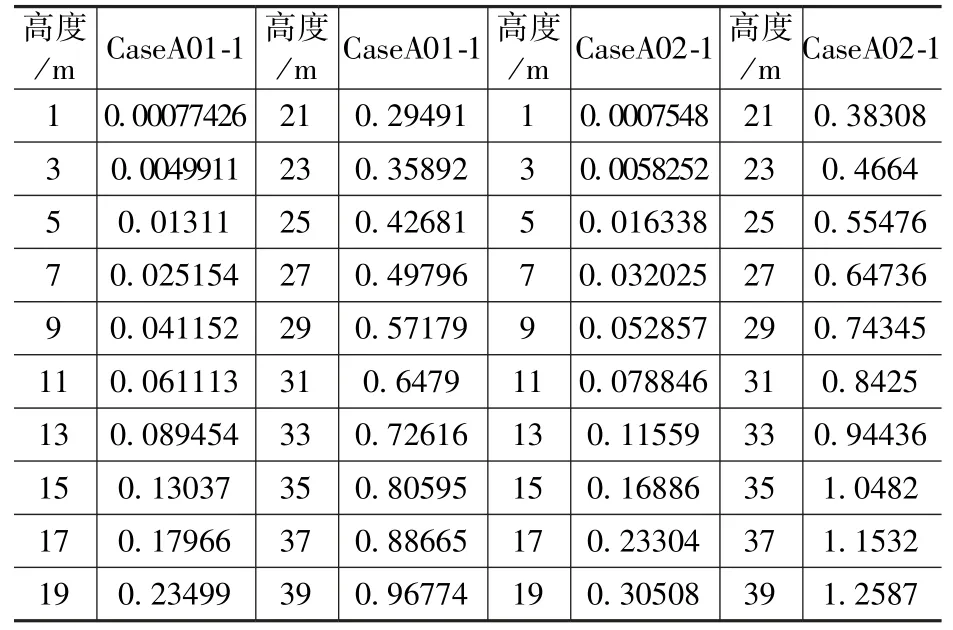
表4 部分工况下的结构模态位移(单位：mm)Tab.4 Structural modal shapes of partial cases(unit:mm)

3 基于BP神经网络的铁塔损伤识别

BP神经网络可以将反问题的映射关系以网络权值的方式保存下来，即将这种关系分布式地存储于网络权值中，而使用者无需关注网络内部具体是如何操作的，而结构的损伤识别是一个典型的由果求因的问题，结构的损伤会引起其动力特性及响应的变化，因此BP神经网络常常用来做结构的损伤识别，BP神经网络输入参数的选择及其表达形式将直接影响损伤识别结果，输入参数必须包含损伤位置信息与损伤程度信息，且受环境影响较小。Kaminski应用固有频率的相对下降量NFRi来识别损伤的位置[12]，识别的结果较好，其计算公式如下:

式中:NFRi为第i阶固有频率的变化率；ωui为健康状态下的结构的第i阶固有频率；ωdi为损伤结构的第i阶固有频率。

计算CaseA、CaseB、CaseC三种工况下NFRi值，由于篇幅限制，仅列出CaseA工况下计算结果，见表5。

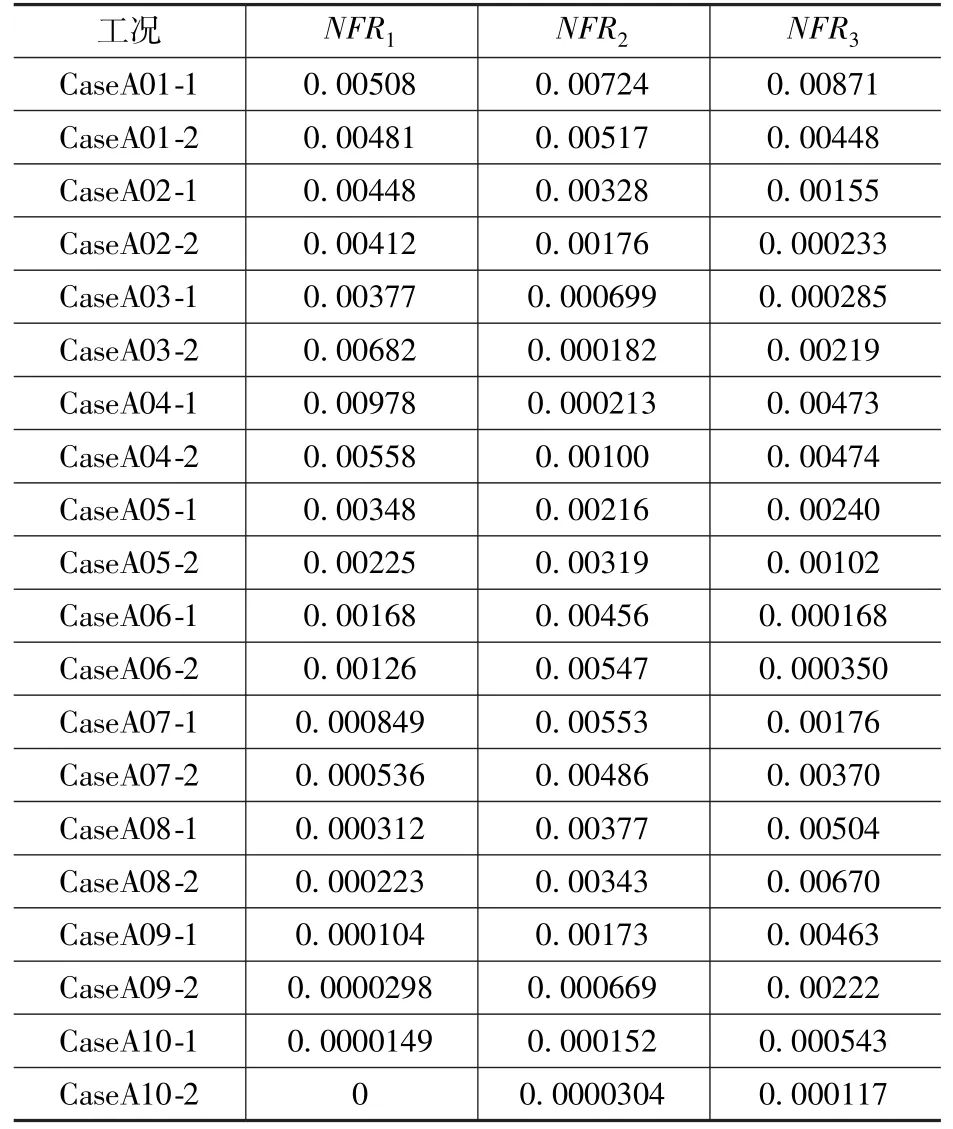
表5 CaseA工况下的NFRi值Tab.5 NFRi under CaseA

由表5可知，随着损伤位置的增高，NFR1整体呈下降趋势，但CaseA03-2、CaseA04-1、CaseA04-2等工况出现误判的情况，NFR2、NFR3无规律变化，无法识别出损伤，因此仅通过NFR无法准确识别出单管通信塔结构的损伤位置。

损伤识别量DS被证明其取决于损伤位置而与损伤程度无关[13]，DS的计算公式为:

式中:{DS}i为第i阶模态的损伤指标向量；{ΔΦ}i为第i阶模态振型的变化量；Δω2r为第r阶模态频率平方变化量(一般取第一阶模态频率变化)。

随机选取二阶模态位移来构造损伤识别量，由于篇幅限制，仅列出CaseC02-1工况下的损伤识别量值，见表6。

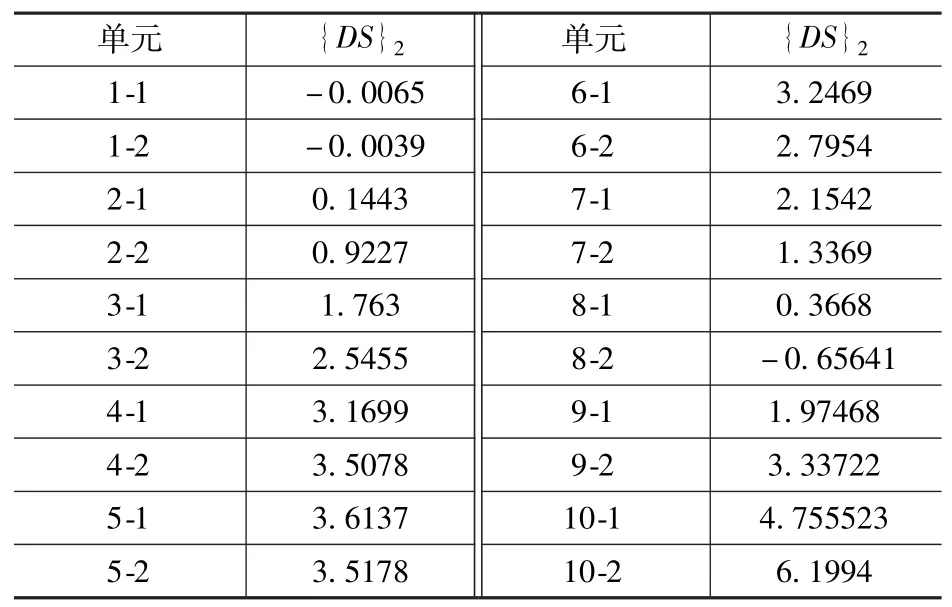
表6 CaseC02-1工况下的损伤识别向量DSTab.6 Damage identification vector DS under CaseC02-1

NFRi与DS参数只与损伤位置有关而与损伤程度无关，所以为了能够同时对损伤程度标定，在输入参数中补充反映结构损伤程度的量频率ω。随机选取了除CaseA04-2、CaseB06-2、CaseC03-1、CaseC07-2外的其余工况下的53组数据作为BP神经网络的训练样本，CaseA04-2、CaseB06-2、CaseC03-1、CaseC07-2这四组作为网络的验证样本。网络输入向量为{NFR，DS，ω}，网络输出向量为{Y1，Y2，…，Yi}，式中Yi表示结构在i单元处的损伤，如:1单元损伤10%、20%、30%，则Y1分别为0.1、0.2、0.3，以此类推，由于神经网络的输出向量会具有一定的误差，因此本研究认为当输出结果值大于0.05时为损伤发生的真分量，反之则为伪分量，可以忽略不计。利用MATLAB软件编程进行BP神经网络的样本计算，由于篇幅限制，表7只列出部分工况识别结果。

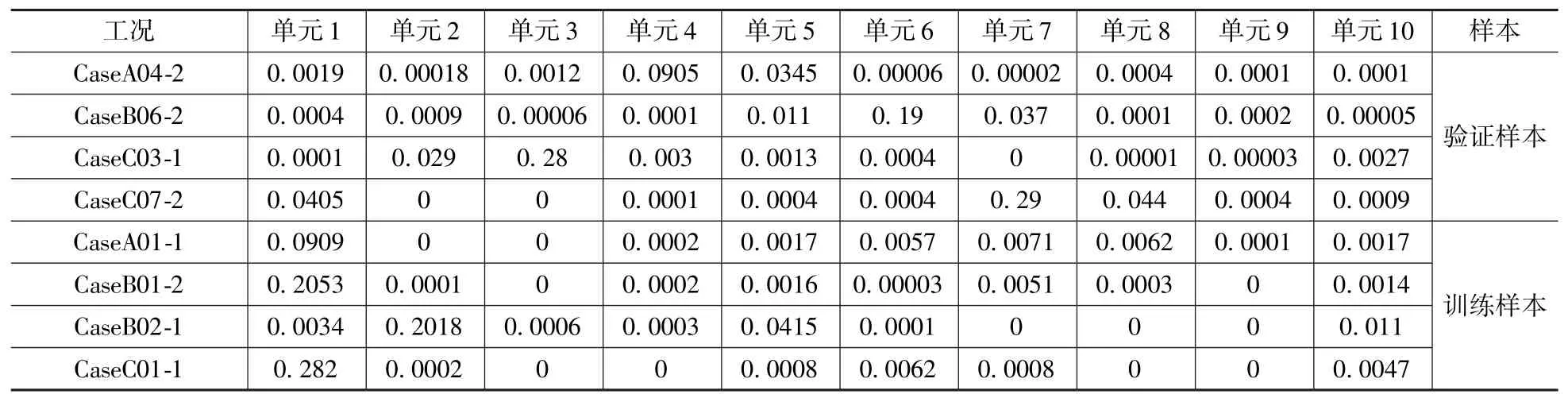
表7 基于BP神经网络的损伤识别结果(部分)Tab.7 Damage identification results based on BP neural network(partial)

由表7结果可知，BP神经网络识别出CaseA04-2工况下4号单元损伤9.05%，CaseB06-2工况下6号单元损伤19%，CaseC03-1工况下3号单元损伤28%，CaseC07-2工况下7号单元损伤29%，与实际情况相符，均准确识别出通信单管塔的损伤，未出现识别异常的情况。因此将频率及振型和频率的组合参数NFRi、{DS}i、ω作为BP神经网络的输入向量能较好地识别单管通信塔结构的损伤，也就是基于BP神经网络的铁塔损伤识别是可行的。