“数形结合”探秘绝对值
2020-11-05文张文珠
文张文珠
著名数学家华罗庚先生曾经说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休。”对绝对值的探究过程,“数轴”充当了桥梁的作用。绝对值借助数轴来表达,充分体现了数学中“数形结合”的思想精髓。接下来,让我们开始一场绝对值的探秘之旅。
一、整装待发——理解绝对值的几何意义
数轴上表示一个数的点与原点的距离,叫做这个数的绝对值。
“数a 的绝对值”记作 ||a ,几何意义为数轴上表示数a的点与原点的距离。
例1如图1,| |-3 的几何意义为数轴上表示-3的点与原点的距离。

图1
二、脚踏实地——探秘任务一:两数差的绝对值
“两数差的绝对值”记作|a - b|(a、b是常数),几何意义为数轴上表示数a 和数b 的两个点之间的距离。
例2如图2,|5- 2| 表示5 与2 的差的绝对值,实际上可以理解为5与2两数在数轴上所对应的两点之间的距离;由计算可得|5- 2|=3;由数轴可得5 与2 两数在数轴上所对应的两点之间的距离是3,所以|5- 2 |=3。

图2
如图3,|5+2|即|5-(-2)|,表示5 与-2的差的绝对值,实际上可以理解为5 与-2 两数在数轴上所对应的两点之间的距离。由计算可得|5+ 2 |=7;由数轴可得5 与-2 两数在数轴上所对应的两点之间的距离是7,所以|5+2|=7。

图3
经验升级:用数学语言表示“两数差的绝对值”,两数之间要用运算符号“-”号连接,若遇到两数之间用“+”号连接,需要转化为“-”号。
三、登高望远——探秘任务二:两距离之和的最小值
“两距离之和”记作|x-a|+|x-b(|x 是未知数,a、b 是常数),可以理解为数轴上表示x 的点(动点)分别与表示a、b 的点(定点)之间的距离之和。
例3求|x+1|+|x-5|的最小值。
【解析】原式写成两数差的绝对值为|x-(-1)|+|x-5 |,可以理解为数轴上表示x的点(动点)分别与表示-1、5 的点(定点)之间的距离之和。因为x 的不确定性,可以利用数轴画出表示-1、5 的两个定点,然后分类讨论如下:
1.表示数x 的点在表示-1 的点左侧,两距离长如图4所示:

图4
2.表示数x 的点在表示-1 和5 的两点之间(包括两点),两距离长如图5所示:

图5
3.表示数x 的点在表示5 的点右侧,两距离长如图6所示:
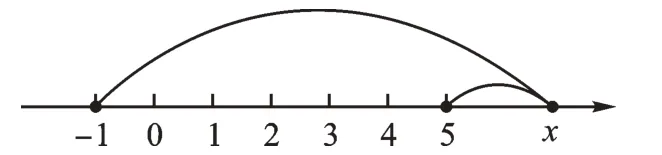
图6
由图可知,当数轴上表示数x 的点位于表示数-1 和5(包括-1 和5)两点之间时,|x+1 |+|x - 5 |取得最小值,最小值就是表示数-1和5 两点之间的距离(|-1)- 5 |=6(见“探秘任务一”所得结论)。所以|x + 1 |+|x - 5 |的最小值是6。
经验升级:求两距离之和的最小值,首先将原式写成两数差的绝对值;其次理解式子的几何意义,借助数轴画出定点;最后利用数形结合对动点的不同位置分类讨论,得出最短距离和即为所求最小值。
四、手摘星辰——探秘任务三:多个距离之和最小值
“多个距离之和”记作|x - a1|+|x - a2|+…+|x -an(|x 是未知数,a1、a2、……、an是常数),可以理解为数轴上表示x 的点(动点)分别与表示a1、a2、……、an的点(定点)之间的距离之和。
例4求|x - 1 |+|x + 2 |+|x - 3 |的最小值。
【解析】原式写成两数差的绝对值为|x - 1 |+|x -(-2)|+|x - 3 |,可以理解为数轴上表示x的点(动点)分别与表示1、-2、3的点(定点)之间的距离之和。如图7,因为x 的不确定性,可以利用数轴画出表示1、-2、3 的三个定点,然后分类讨论,可得:当x=1 时,|x - 1|+|x + 2 |+|x - 3 |的最小值是5。
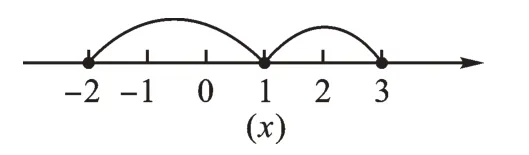
图7
例5求|x- 1 |+|x + 2 |+|x - 3 |+|x + 4 |的最小值。
【解析】数形结合分类讨论后,如图8 从数轴上可以看出最小值就是表示数-2和1两点之间的距离与表示数-4和3两点之间的距离之和,记作|-2 - 1 |+|-4 - 3 |=10。所以,当x 在-2 与1 之间(包括-2 和1)时,|x - 1 |+|x + 2 |+|x - 3 |+|x + 4 |的最小值是10。
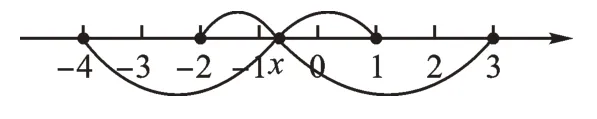
图8
经验升级:若数轴上有奇数个定点,则当动点在最中间的定点时,原式有最小值,再借助数轴求出最小值;若数轴上有偶数个定点,则当动点在最中间两个定点之间(包括这两点)时,原式有最小值,再借助数轴求出最小值。
在这场绝对值的探秘之旅过程中,“数轴”功不可没,它带领我们把一个非常抽象的问题进行了直观展示,帮助我们理解了“绝对值”的本质,数形结合贯穿于整个探秘之旅中。绝对值的探秘之旅告一段落,前方还有更加精彩的数学世界等着同学们去探索。
