温湿环境下棉织物的抗皱性能变化规律及其预测模型

姚金波，王志意，董 敏，姜会钰，唐秀琴

（1.武汉纺织大学 生物质纤维及生态染整湖北省重点实验室，武汉430200；2.武汉纺织大学 湖北省服装信息化工程技术研究中心，武汉430200）

棉纤维主要成分是纤维素，是由β-葡萄糖苷键与脱水D-六环葡萄糖所组成的线性多糖，分子组成为（C6H12O5）n，是自然界中重要的天然纤维素材料[1-4]。棉织物因具有柔软保暖、吸湿透气等优良特性而广受消费者的喜爱，但棉织物易起皱变形，严重影响了棉织物的服用性能，也给消费者带来诸多不便，因此，常需进行防皱整理加工，以赋予织物一定的保形性能。

在保形抗皱的长期研究过程中，学者们主要从棉纤维微观分子结构（无定形区）出发，通过促进整理剂与棉纤维大分子间的共价交联，减少纤维发生形变时因氢键断裂而导致的蠕变和不可恢复形变[5-10]。虽然从抗皱整理的角度出发直接解决了已产生或将产生的褶皱问题，达到了抗皱的目的，但却对织物在不同应用环境条件下产生褶皱的原因未做更多研究。因此，从棉织物的应用环境和整理加工出发，研究在不同应用环境下棉织物的保形性变化规律具有重要意义。

湿、热环境是棉织物应用的主要环境，也是导致织物保形性变差的重要原因之一。当纤维处于高湿环境时，水分子进入到纤维无定形区，破坏分子链段间的氢键，减弱纤维分子间的氢键结合力，而且大量水分子的进入促使纤维发生溶胀，使纤维大分子间的内聚力进一步减小，导致纤维分子链段间易于相对滑移，引起纤维变形。此时，如果该变形能够维持一定的时间，则纤维大分子链段间会重构新的氢键，使形变暂时稳定，这也是棉织物形成折皱的根本原因。此外，纤维含湿量越大，则导热系数越大，在受热时向纤维内部传递的热能越多，会促进纤维大分子链段热运动，甚至纤维的聚集态结构和形态结构也会产生一些变化，从而使纤维的保形能力进一步恶化[11-12]。

一般地，对于热塑性纤维，热作用在纤维外观形态上最主要表现为热收缩，是纤维内部应力释放和解取向共同作用的结果[13-18]。但对于亲水性的棉纤维，水分子恰恰起到了增塑作用，显然湿、热的共同作用使得棉纤维易于产生变形。另外，在低温环境下，棉纤维大分子链段被“冻结”，而纤维内部水分冰晶化时体积增大，会引起纤维表面形态变化，但当温度再度恢复到常温时，纤维内部被冰晶胀大的孔洞和缝隙将会被保留，进而影响纤维的结构和性能[19-23]。

因此，明确湿、热协同环境对棉织物保形能力的影响规律，并预测抗皱性能失效条件，显然能够有针对性地改进树脂抗皱整理工艺、指导消费者合理使用抗皱棉制品。对此，本文在探究湿、热环境对棉织物保形性影响规律的基础上，建立抗皱棉织物在不同温、湿度条件下的折皱回复性能预测模型。

1 试验部分

1.1 材料与仪器

原料：经液氨丝光、荧光增白处理后的白色纯棉平纹机织布，经纬密度为160根/（10 cm）×72根/（10 cm），山东鲁泰纺织股份有限公司产品；低甲醛树脂DM-3510、催化剂C-8，均为广东德美精细化工股份有限公司产品。

仪器：PMT-350型连续式浸轧拉幅定型机，厦门瑞比精密机械有限公司产品；YG541E型激光织物折皱弹性测试仪，宁波纺织仪器厂产品；ZY/GDJS-400L型高低温环境试验箱，无锡中亚环境实验设备有限公司产品；折皱回复角测试支架，按照GB/T 3819-1997《纺织品/织物折痕回复性的测定/回复角法》标准自制。

1.2 试样制备

选用DM-3510低甲醛树脂整理剂，以浸轧—烘燥—焙烘工艺，对棉织物进行抗皱整理，选取5组抗皱效果差异较大的布样作为分析试样，研究温湿环境对织物保形性的影响。5组织物保形特征如表1所示。

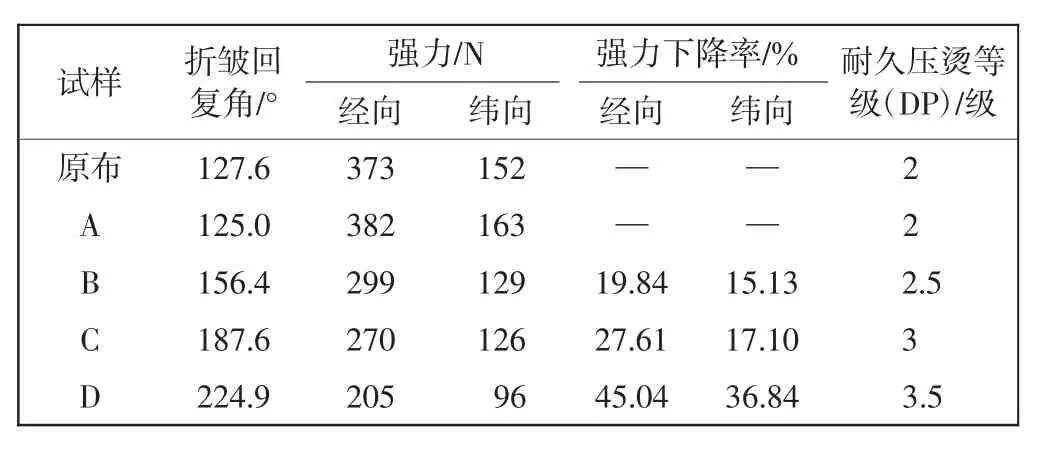
表1 5组试样的保形特征Tab.1 Conformal characteristics of five groups of samples

1.3 实验方法

调节高低温环境试验箱的温、湿度，达到实验设计的水平，将5组试样放入环境试验箱中平衡2 h后，按照GB/T3819-1997《纺织品/织物折痕回复性的测定/回复角法》中的织物折皱回复性垂直测定方法，测试对应条件下试样的折皱回复角。

2 结果与讨论

2.1 温度对棉织物保形性的影响

不同湿度条件下的试样折皱回复角随温度变化的情况如图1所示，其拟合方程如表2所示。

由图1可见，在一定湿度下，试样的折皱回复角在常温25℃附近最大，高于常温时，则会随着温度升高而减小；低于常温时，则会随着温度降低而减小。从下降趋势来看，试样在低温条件下受到的影响比高温时严重。这是因为在低温环境下，棉纤维分子链节和链段被“冻结”，变形或位移的大分子链段难以通过热运动的方式恢复到原状，即表现为折皱回复角降低；而且当温度低于0℃时，除大分子链段的变形难以恢复之外，纤维内部水分冰晶化导致体积增大，进而引起纤维聚集态结构和形态结构变化，最终使回复角进一步降低，这种现象会随着环境湿度增加而加剧。当温度较高时，纤维大分子链段热运动加剧，纤维变形能力增强，而对应地因变形而带来的内应力也易于消除，最终表现为易于形成折皱且难以自由回复原状。这种现象也随着环境湿度的增加而有所增加，很显然水分子会加强变形或位移后的大分子链段之间所建立的新的氢键联系，结果使织物形成相对稳定的皱褶，即折皱恢复能力降低。

从图1中曲线的斜率变化也可以看出，树脂整理越强烈即DP等级、折皱回复角越高的试样受温度影响的变化幅度也越大，且湿度增加时其变化幅度也会稍有增加。这种现象可能与树脂整理剂在纤维内部的可及度及其均匀性有关。在树脂整理过程中，树脂对棉纤维内部无定形区的可及区域是有限的，其仅能进入充分膨化的无定形区域，当可及区域交联够充分时，织物则获得高折皱回复角，但当温度与湿度产生变化时，受前文作用机制的控制，来自不可及区域（即未交联无定形区域）的影响将会显现出来，使得折皱回复角出现较大幅度的下降。由此可以推测，提高树脂整理剂对棉纤维无定形区域的可及度是提高抗皱整理织物耐温、湿度稳定性的重要途径之一。

图1 不同湿度条件下试样折皱回复角随温度变化的曲线Fig.1 Change curves of crease recovery angle of fabric with temperature under different humidity conditions

2.2 湿度对棉织物保形性的影响

不同温度条件下试样折皱回复角随湿度变化的情况如图2所示，其拟合方程如表3所示。

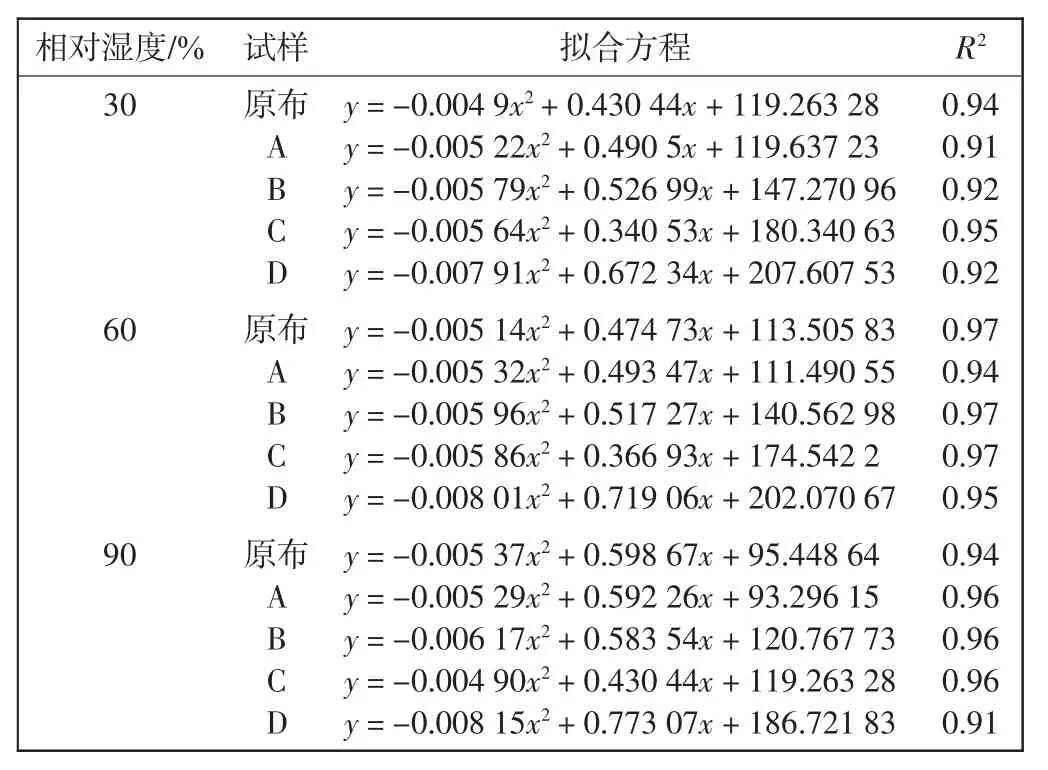
表2 不同湿度条件下试样折皱回复角随温度变化曲线的拟合方程Tab.2 Fitting equations of change curves of crease recovery angle with temperature under different humidity conditions

由图2可知，试样在一定温度下的折皱回复角随着湿度的升高而发生不同程度的下降。在图2（a）的低温度环境下，随着环境相对湿度的增加，因水分子的结晶化作用，导致折皱回复角的下降幅度增加，且各试样的变化幅度相近。在图2（b）、图2（c）的温度环境下，随着湿度的升高，原布、试样A两组试样折皱回复角随湿度升高而下降的幅度很小。这是因为原布、试样A两组试样的抗皱整理等级很低，分子间交联程度低，织物仅具有很低的折皱回复角，因此，其随湿度变化的降低幅度较小。与试样B、C相比，抗皱等级最高的试样D折皱回复角随湿度增加时的下降幅度小，这是因为试样D的纤维大分子间交联程度高，高温下的链段回复能力强，因此，表现出较好的耐湿度变化稳定性。

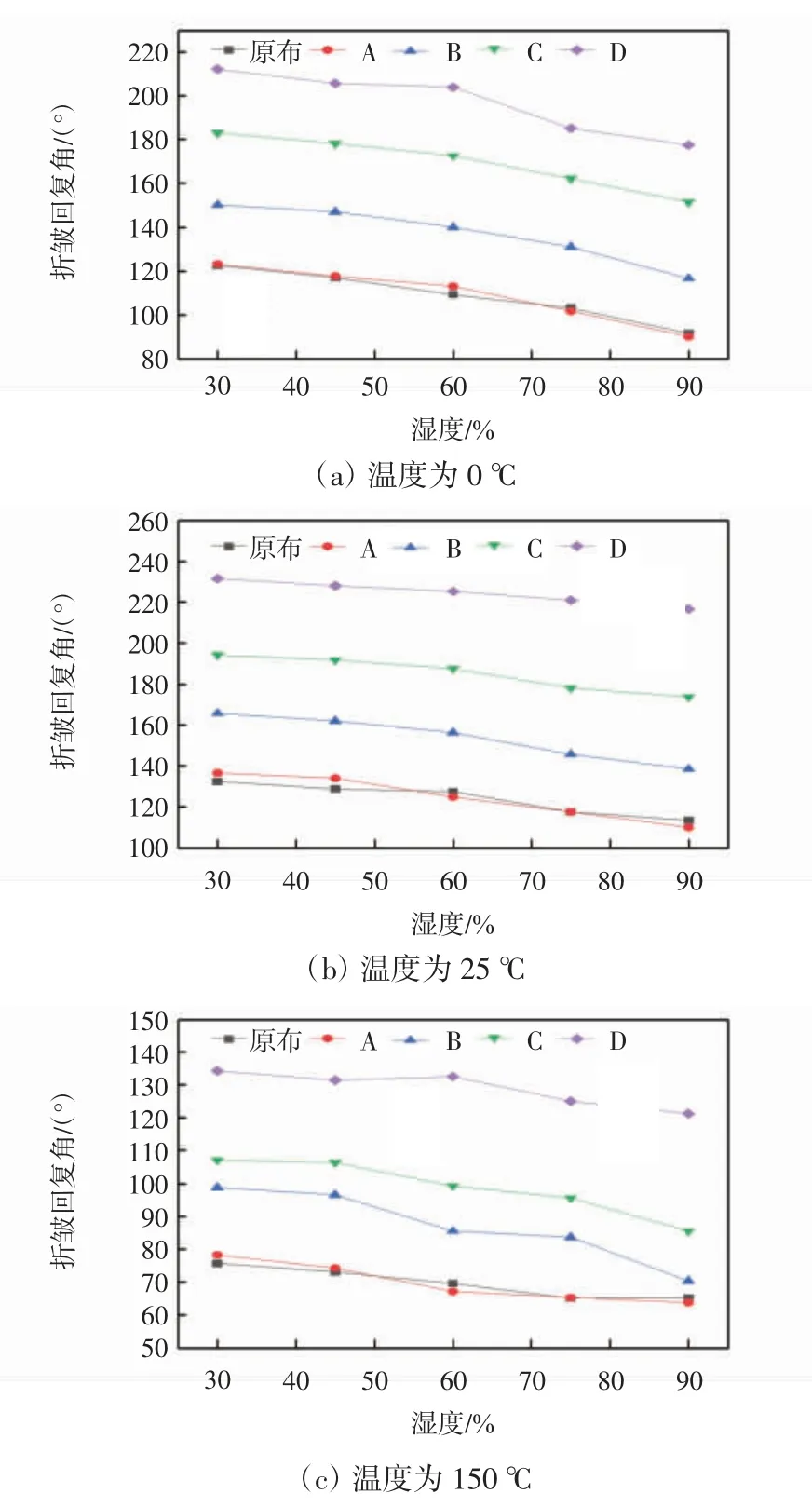
图2 不同温度条件下试样折皱回复角随湿度变化的曲线Fig.2 Change curves of crease recovery angle with humidity under different temperature conditions

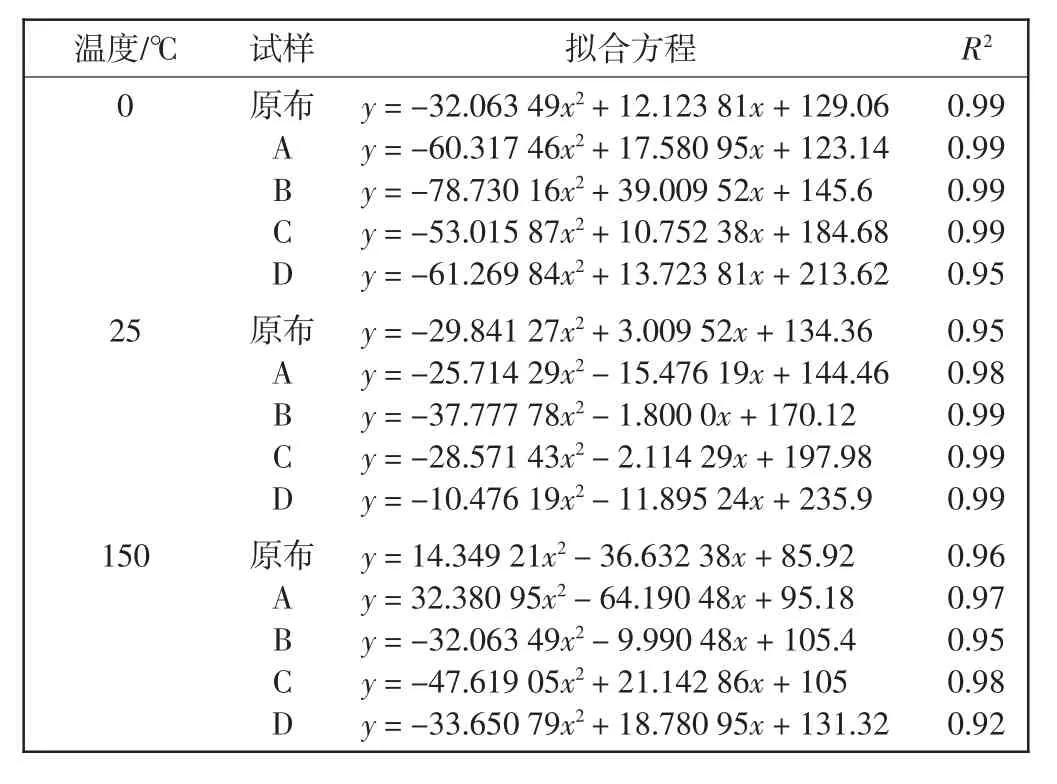
表3 不同温度条件下试样折皱回复角随湿度变化曲线的拟合方程Tab.3 Fitting equations of change curves of crease recovery angle with humidity under different temperature conditions

由此可见，湿度对抗皱棉织物的抗皱保形性影响程度低于温度的影响。

2.3 温、湿复合环境下织物保形能力的预测模型

由上述可知，温度、湿度对棉织物保形性的影响规律十分复杂，并非是简单的线性关系。因此，以温、湿复合环境下的织物折皱回复角作为因变量，试样抗皱水平、温度、湿度作为自变量，并以25℃、相对湿度（RH）60%的标准环境条件下（以下简称标准环境）测得的折皱回复角表示该试样的抗皱水平，利用SPSSAU系统建立多元非线性回归分析预测模型，研究温、湿复合环境下棉织物保形能力的预测模型。由于任一函数关系都可以用多项式逼近，因此，本文采用式（1）中的二次多项式建立模型。

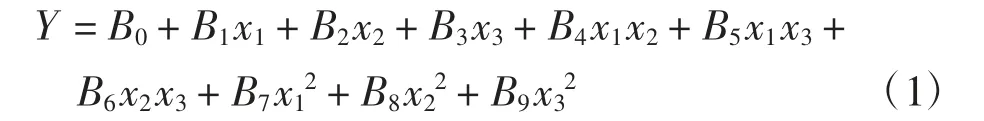
式中：Y为预测环境下的织物折皱回复角；x1为试样在标准环境条件下测得的折皱回复角；x2为预测环境的温度；x3为预测环境的相对湿度。

为方便运算，令x4=x1x2；x5=x1x3；x6=x2x3；x7=x12；x8=x22；x9=x32。则模型（1）转化为线性模型（2）：

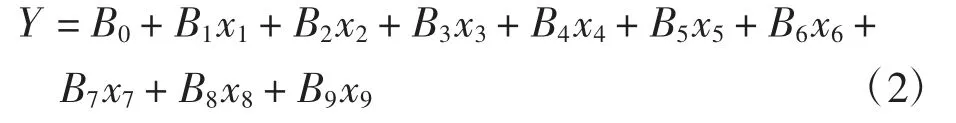
本文选择5种不同抗皱水平的面料，依据抗皱整理棉织物的常规应用环境特点，分别测试试样在温度为0、25、80℃和相对湿度为30%、45%、60%、75%、90%的不同组合条件下的折皱回复角，获得75组实验数据。其中，60组作为训练集、15组作为测试集。将训练集数据输入回归模型，其结果如表4所示。

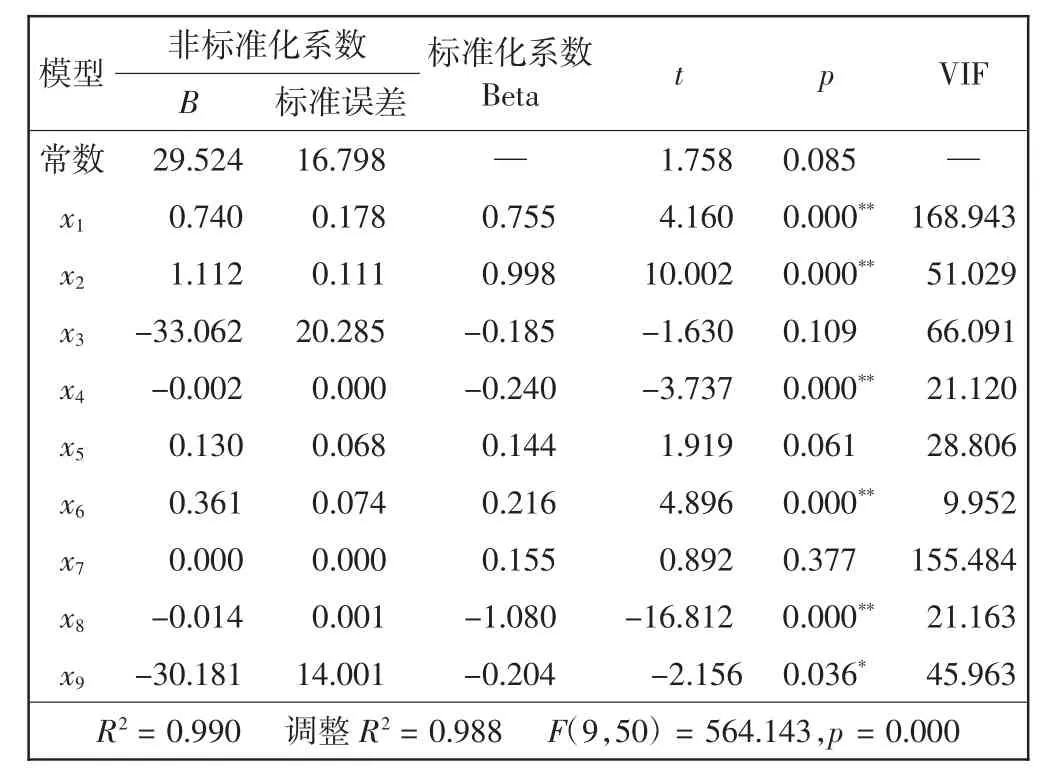
表4 线性回归分析结果Tab.4 Results of linear regression analysis

由表4可知，模型R2为0.990，表明所有自变量可以解释Y99.0%的变异量，且模型通过F检验（F=564.143，p=0.000＜0.05），说明x1、x2、x3、x4、x5、x6、x7、x8、x9中至少有1项对Y产生影响关系。但是，由于多数自变量的方差膨胀因素VIF值大于10，说明选定的9个自变量间存在较强的多重共线性问题。因此，进一步采用逐步回归分析法进行解析，结果如表5所示。

表5 逐步回归分析结果Tab.5 Results of stepwise regression analysis

由表5可知，数据经逐步回归处理后，不具有显著性的自变量x3、x5、x7被移出模型，此时的模型R2为0.989，说明x1、x2、x4、x6、x8、x9可以解释Y98.9%的变异量，且模型通过F检验（F=816.622，p=0.000＜0.05）。但是，模型中仍有个别变量的VIF值大于10，表明逐步回归后仍存在多重共线性问题。因此，进一步使用岭回归解决共线性问题，而后再对模型进行分析，结果如表6所示。

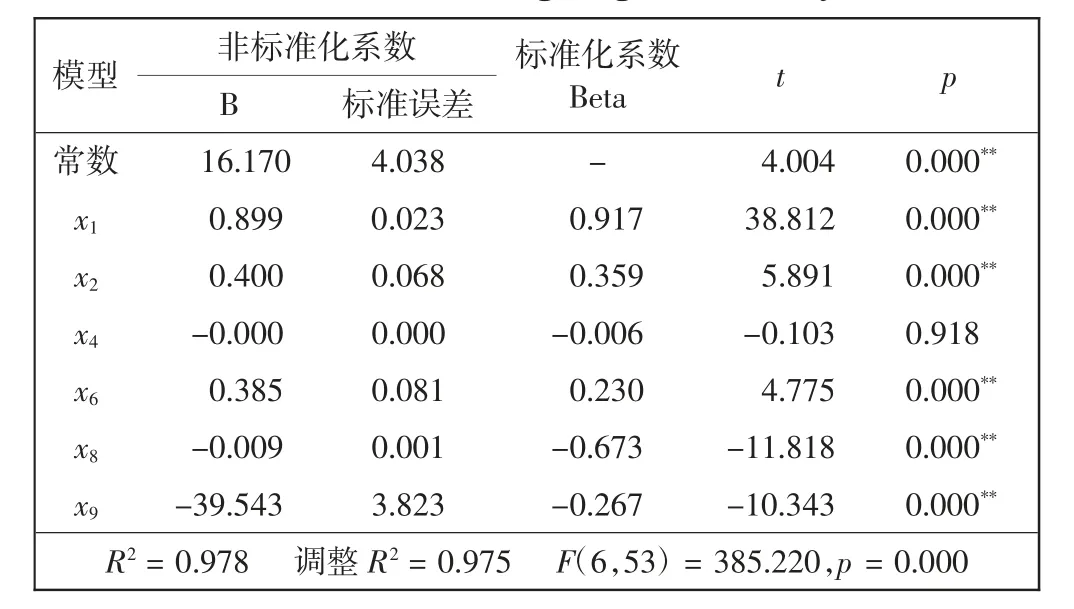
表6 岭回归分析结果Tab.6 Results of ridge regression analysis

由表6可知，x4的非标准化系数为0，且未通过相关性检验），将被删除，其余变量均通过相关性的t检验（p＜0.01）。另外，模型R2为0.978，说明最终选择的自变量x1、x2、x6、x8、x9可以解释Y97.8%的变异量，且模型通过F检验（F=385.220，p=0.000＜0.05）。由此得到最终的回归模型为：

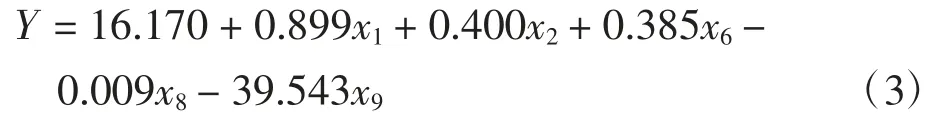
即：

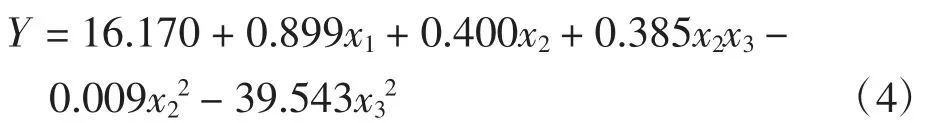
利用测试组数据对该模型进行验证，结果如表7所示，残差的标准差为5.295 5。

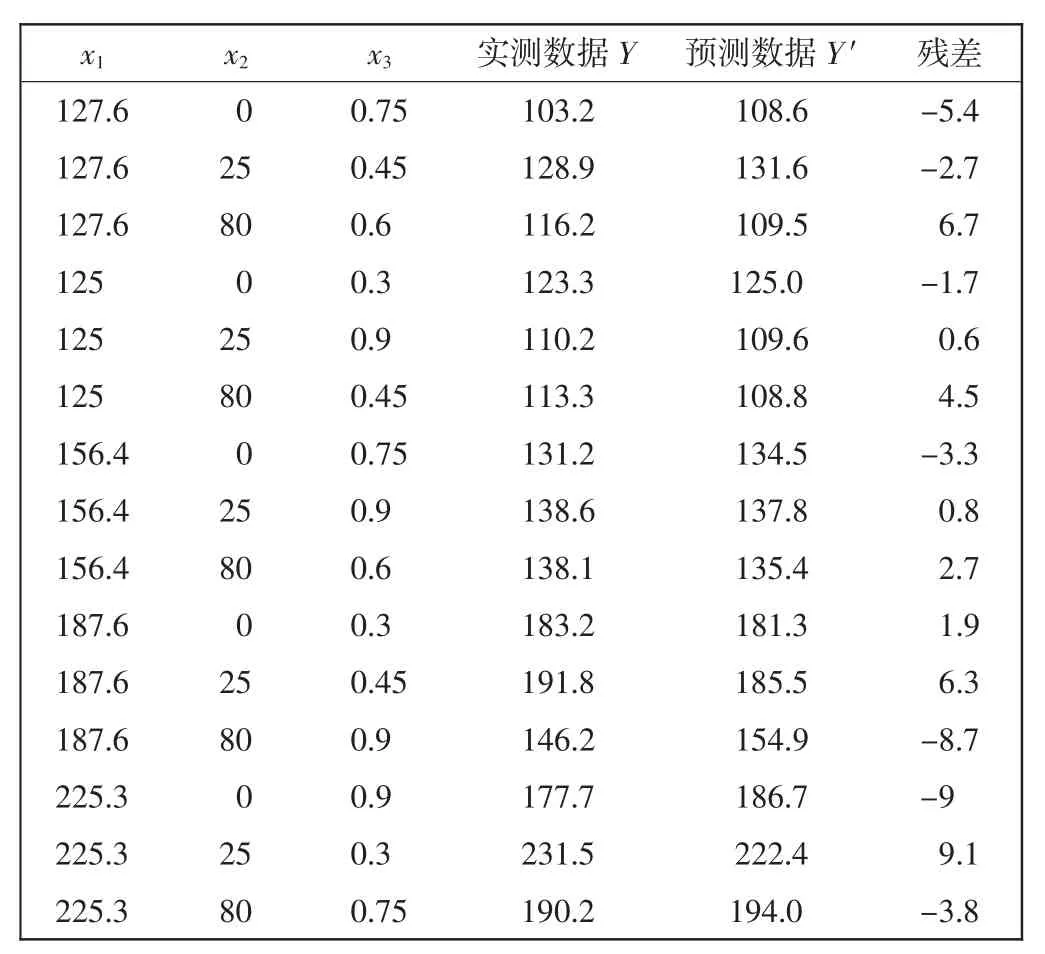
表7 模型验证结果Tab.7 Results of model validation

由表7数据作残差散点图，如图3所示。

图3 预测值与真实值的残差散点图Fig.3 Scatter plot of residuals between predicted and actual values

由图3可以看出，散点分布在“0”直线的上下方，残差绝对值均在3倍标准差以内，并无异常点，表明该模型有效，其拟合和预测效果较好。

为进一步说明温、湿复合环境对织物保形性的影响程度，可使用因变量Y的全微分公式（5）进行表达：

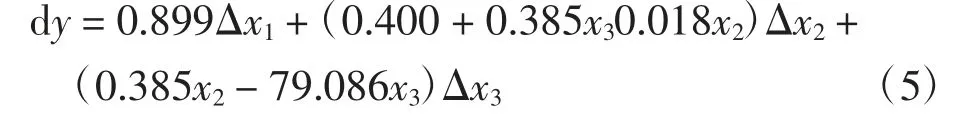
式（5）中，各变量改变量的系数代表了折皱回复角改变量随该变量变化时的变化率。由式（5）可见，试样的折皱回复角改变量对于标准环境下的折皱回复角的变化率为正，即随标准环境下折皱回复角的增加而增加，显示出织物耐温、湿度变化的保形能力与自身获得的抗皱整理水平密切相关，自身的抗皱水平越高，则在温、湿度变化时也可以保持高的保形能力。

环境温度越高，折皱回复角随温度变化的幅度减小，而提高环境湿度则加剧这一变化，使变化率增大。环境湿度越高，折皱回复角随湿度变化的幅度减小，而提高环境温度则使得织物折皱回复角的变化率增大。可见，温度、湿度对织物保形性能的交互影响关系十分复杂。本文所建立的预测模型，通过检验证实，能够有效预测温、湿复合环境下织物的保形变化情况，且模型公式也体现出温、湿复合环境对织物保形性的交互影响特征，反映出的变化规律与实验分析结论相一致。

3 结论

（1）温度、湿度对抗皱整理棉织物的保形性能会产生不同程度影响，与标准条件下相比，高温或低温环境都将使织物抗皱性能下降，单纯的湿度变化对抗皱保形性影响较小，但两者的交互影响却使得抗皱保形性恶化。这种变化原因主要与抗皱整理剂的可及区域、不可及的无定形区域大分子链段的热运动、氢键等因素有关，抗皱等级越高的棉织物，在非标准条件下虽具有较好的折皱恢复性，但其降低幅度也较大。

（2）通过非线性回归分析，得到试样抗皱水平（标准条件下的折皱回复角）、环境温度、环境湿度与温/湿复合环境下织物的折皱回复角之间关系的预测模型。模型的R2为0.978，且模型通过F检验（F=385.220，p=0.000＜0.05），说明模型有意义，模型预测值与真实值的残差绝对值均在3倍标准差以内，证实该模型拟合和预测效果较好。因此，本模型可以以标准条件下的折皱回复角为基础，预测出经轧烘焙工艺整理后的织物在0～80℃温度区间和RH30%～90%湿度区间环境下的折皱回复角，进而判定织物耐温、湿度变化的保形稳定性。