基于数列极限教学内容的变革与实践

程小静

(陕西理工大学，陕西 汉中 723099)

极限贯穿高等数学内容的始终，其中数列极限[1]是初学高等数学最难理解而又重要的问题之一，是学生从初等数学到高等数学不得不跨越的门槛，因此，很多课堂创新、教学模式变革[2]的探索都以数列极限为例，因此，数列极限非常重要，相对于数列极限无穷小数列就容易理解多了。本文针对这一教学重难点采取首先引入无穷小数列的定义与性质，再由无穷小数列的定义给出数列极限的定义，结合无穷小数列的性质讨论数列极限的性质，来分散难点，是对高等数学内容尝试的一种新的教学模式和变革。

1 无穷小数列的定义和性质

1.1 无穷小数列的定义

②关于ε：具有二重性，即任意性、相对固定性。

③关于N：特定的项数与ε有关。

⑥无穷小数列的几何意义：任给ε>0，总能找到正整数N，使从第N+1项开始中的所有项都落在0的ε领域内，这表明无穷小数列从某项起越来越密集在0的任意邻近，而在这邻域之外至多有N项：(见图1)。

图1 无穷小数列的几何意义

1.2 无穷小数列的性质

1.2.1 无穷小数列必有界

首先，说明数列有界性的定义。

其次，证明性质无穷小数列必有界。

1.2.2 有限个无穷小数列的和、差、积仍为无穷小数列

以两个无穷小数列的和仍为无穷小数列为例证明.

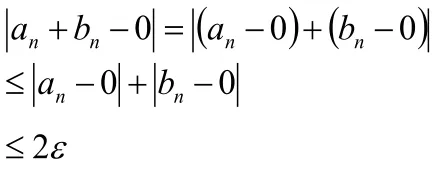
1.2.3 常数或有界数列与无穷小数列的乘积仍为无穷小数列

以有界数列与无穷小数列的乘积仍为无穷小数列为例证明。

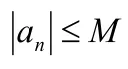
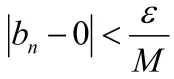
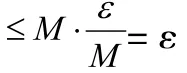
说明有界数列与无穷小数列的乘积仍为无穷小数列，常数与无穷小数列的乘积仍为无穷小数列类似证明。

2 数列极限的定义和性质

2.1 数列极限的定义

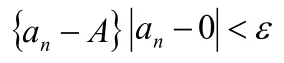
②关于ε，N同无穷小数列定义中的相同。

④数列极限的几何意义。这里借助无穷小数列定义的几何意义完全可以尝试让学生自己总结数列极限的几何意义，注意强调数列极限存在与否同样与数列的前有限项无关。

2.2 数列极限的性质

2.2.1 收敛数列的极限是唯一的

为无穷小数列，说明A=B故收敛数列的极限是唯一的。

2.2.2 收敛数列是有界的

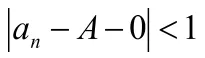
3 解决数列极限实际教学中存在的困难

尽管对于数列的研究大多是通过算式来表述的，但算式的表述在教学中有时并不能非常地直观说明数列的性质，所以，需要借助文字来描述数列极限，在教学中做到使学生可以深入认知数列极限，让学生观察数列动图，以求对数列进行定性描述。

如果用语言描述的方法概括数列极限现象，得到：

对于数列极限的描述都是从已知到未知进行的，在这一过程中伴随着简单到复杂的现象。在教学实践过程中，尽管数列极限对于学生来说是一个全新的概念，但在描述数列极限过程中运用到的绝对者不等式却在较早以前的学习中就有涉及到，并不复杂。绝对值不等式的表示在数列极限中是一个关键的因素，可以认为，数列极限事实上就是初级绝对值不等式的实际应用。为排除学生在学习数列极限过程中的困难，可以带领其去认知数列极限和ε-N的演变过程，所以，在教学实践过程中定义数列极限大致可分为四步，即将数列极限教学分为几个分步骤进行，在教学过程中教师不应该直接给出数列极限的定义，而是通过每一个步骤与学生共同探索。

3.1 对数列的特点进行观察

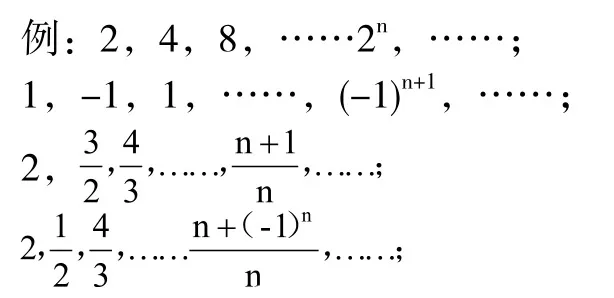
在向学生示例上述算式以后，开始引导其从前所学过的数列知识，最早的数列学习可以回溯到初中数学，但初中数学中的数列学习只涉及到数列的首项、尾项、项数，为初级的等差数列、等比数列等。而在本次学习的数列极限中，更关注的是数列的变化趋势，通过这样的引导使学生主动发现一些数列极限的规律，对于数列知识较为扎实的学生来说，可以很容易发现有的数列极限存在越来越大的变化趋势，有的数列极限处于摆动状态，而有的数列存在趋近于某一常数的现象。为更加直观地引导学生继续分析，教师可以通过数轴将数列标注出来，同时，教师需要对学生发现的规律进行及时地总结概括：部分数列存在一致的现象，例如，随着n的数值不断增加，数值会与常数1越来越接近，此时学生会意识到数列极限的这种现象与曾经学习过的函数单调性、函数奇偶性、函数周期性极为相似，将数列极限与函数性质进行对比，可以发现随着n的无限增大，数列值会与某一常数无限接近。

3.2 引用学过知识并及时予以纠正

教师需要纠正学生在数列极限中不可以用“无限增大”“无限接近”等非专业用语，再一次引导学生回忆初中数学中的函数单调性，对于函数单调性的描述为“随着自变量的变化，函数值也随之变化”，在高中数学中，将函数值的变化描述转化为数学语言，即定义区域内的某区间任意点x1，x2，若x1＜x2，则存在f(x1)＜f(x2)或f(x1)＞f(x2)，即将定义过程进行直观描述。由此可以做出如下定义：对于数列和常数A，任意指定正数ε，终有一个时刻恒成立。

3.3 证明数列极限

3.4 深化概念

前三步对于数列极限的定义还仅局限于概念层面，为使学生可以更进一步地了解数列极限的本质属性，需要通过以下几方面强化学生的数列极限认知：

(2)在进行数列极限解析过程中，要求教师重点分析定义中的关键词，并使学生清楚了解定义中每个字在定义中的意义，尤其要重点解释ε的双重性、绝对值的稳定性或相对稳定性，以及N对于ε的依赖性。

(3)教师还可以通过变式教学清楚地表示数列极限的个本质属性，同时，配合数列举例，再配合没有极限的发散例子，以反衬的方式通过非本质属性表现数列极限的本质属性，使学生更加清晰、形象地了解数列极限的本质属性，加深印象。

4 结论

通过引入无穷小数列的定义和性质为数列极限提供了一个新的教学模式与思路，通过具体的无穷小数列引导学生深刻理解任意小正数，进而理解任意小正数与正整数的依赖关系。甚至利用无穷小数列学生可以自己总结数列极限定义的几何意义，完全可以尝试利用无穷小数列的性质来证明数列极限的性质。这一新的教学模式不但使学生更容易掌握数列极限的深层内涵，增加师生间的双向互动，而且对于强化学生自身学习能力，增加学生学习高等数学的兴趣，都是传统教学内容无法比较的。