真空管道车辆、管道与支撑梁垂向动力学性能研究

杨 易, 章佳文, 王卫成,2, 陈海媚

(1.湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙 410082; 2.博世汽车部件(长沙)有限公司,湖南 长沙 410100)

随着社会的进步、生活节奏的加快,人们对于出行和物流配送时间要求逐步提高。21 世纪以来,世界高速交通系统迅速发展,但是航运、铁路、水运和公路运输遇到了自己的发展瓶颈,因此真空管道交通系统(evacuated tube transportation)作为一种新型运输方式被提出,这是由于真空管道车辆具有高速、阻力小、噪音小、安全和能耗低的特点[1]。为实现更高的运行速度,科研工作者需要在新的环境变量条件下研究这一高速运载工具。

真空管道运输系统是一个庞大、复杂的交通系统,零部件种类繁多且构造复杂。1934 年,德国工程师肯佩尔在获得世界上第1个磁浮列车专利时提出，在真空隧道中运行磁浮列车速度可达1 800 km/h。半个多世纪以来,人们总认为真空管道难以实现,极力探索在开敞大气中能使磁悬浮等高速列车运行速度超过1 000 km/h的道路,但无一成功。历史的结论表明,必须回到真空环境的思路上来,才能实现超高速交通的梦想。目前从全球范围来看,真空管道高速交通的设想主要有美国的ETT 系统、瑞士的超高速地铁和埃隆·马斯克提出的hyperloop 3种。美国 ETT公司提出了小型分散的管道汽车模式,管内径与车外径相差很小,管道内压强为0.1 Pa,运行时几乎没有阻力,车辆最高速度可达600 km/h,1条管道的运输量相当于1条80车道的高速公路[2-3];瑞士的超高速地铁比较接近于常规铁路,其管道内压强为10 kPa,较容易实现,速度定为500 km/h,单向运能只有普通铁路的1/2,且全部处于地下,适用于多山地区[2]。美国 ETT公司只是对真空管道运输系统的总体设想进行了介绍,并未对其中列车空气动力学问题进行深入研究;瑞士超高速地铁工程研究的主要课题中虽然包含了高速车辆与管道内的空气动力学问题,但只局限于大气压力为1.01×104Pa、列车运行速度为 400～500 km/h条件下的列车空气动力学特性,且未对真空管道系统的垂向耦合特性进行研究。

埃隆·马斯克提出的低真空加气悬浮模式是一个由支柱支撑、车辆在压强小于100 Pa的封闭管道内超高速运行的系统。管道系统利用真空泵将密闭管道抽成低真空状态,空气储藏室中的空气最终会用于气动悬浮装置。列车底部左、右两边对称分布着2列气垫,其中每列有14块气垫,共28块气垫,以保持列车与管道之间的悬浮间隙[3]。埃隆·马斯克提出的真空管道系统主要是对高速车辆与管道内的空气动力学问题、线路成本和经济性等问题进行研究，而关于真空管道车辆的垂向振动特性的研究尚无先例可循。但真空管道车辆在高速运行时产生的振动和冲击会对管道支柱产生响应,反过来管道支柱的响应又会对车辆垂向振动特性及悬浮车辆乘坐舒适性等若干问题产生影响[4],因此对真空管道车辆中的垂向振动特性的研究是十分必要的。

本文以hyplerloop真空管道车辆及其运行线路为研究对象,对真空管道车辆与管道-支柱的垂向耦合动力学进行研究,对比分析了磁浮车辆在两跨梁上的动态响应。为了适应数值仿真的需要,在建模时根据研究的重点对模型有相应的假设和简化,本文将管道和支柱作为一个整体考虑,基于带二系悬挂的气浮悬架和车辆与管道-支柱振动模型对真空管道车辆垂向振动特性进行研究,并将其特性与磁悬浮车辆进行对比,以此为真空管道车辆的研究提供思路和方法。

1 车桥模型及振动方程的推导

1.1 管道车辆动力学模型

真空管道示意图如图1所示。

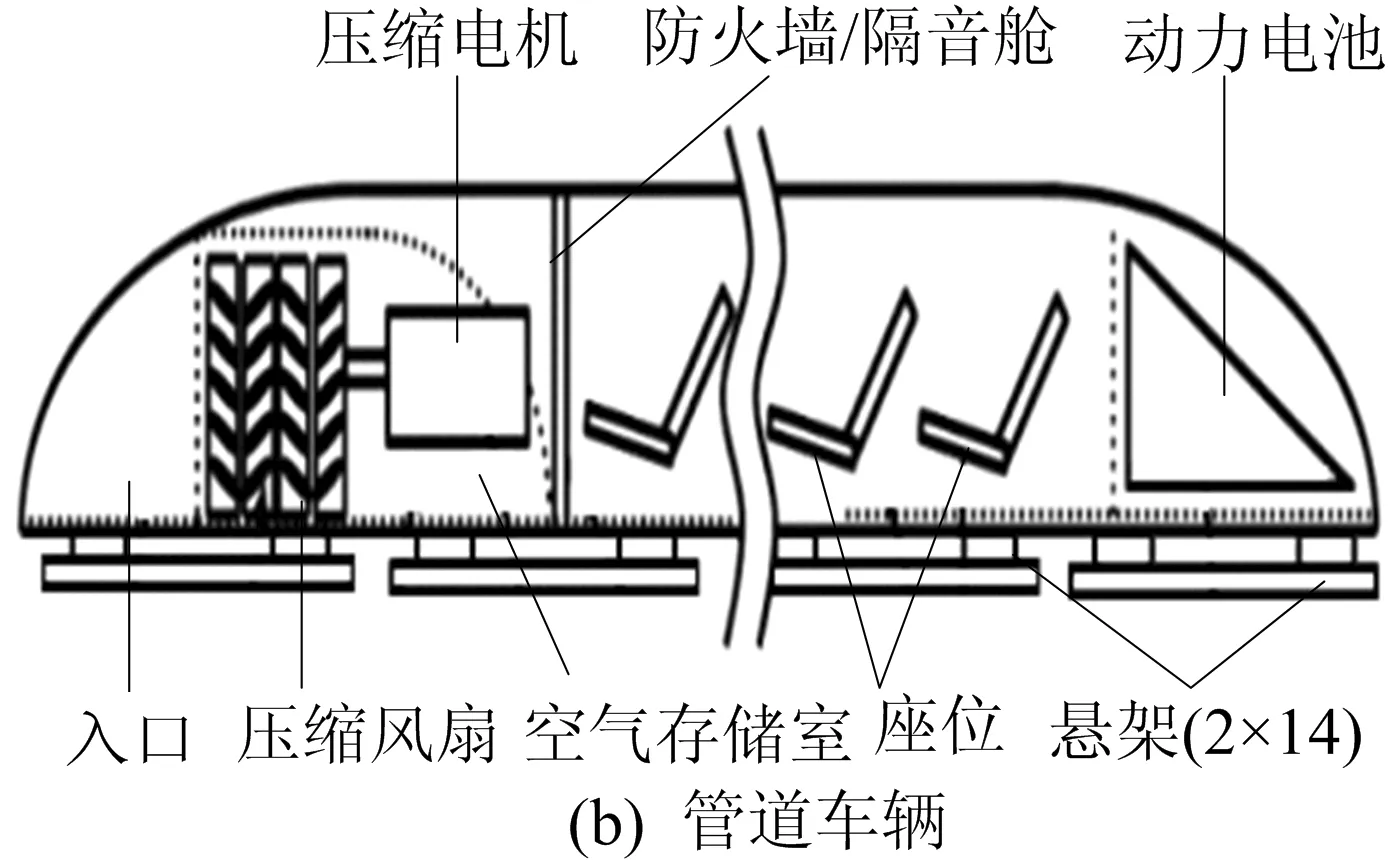
图1 真空管道示意图

真空管道车辆在100 Pa低压环境下的真空管内运行。管道内径为2 230 mm,壁厚为20～25 mm,横截面积为3.91 m2;真空管由钢筋混凝土结构的高架支撑梁支撑,每隔30 m设置1根支撑梁;真空管道车辆底部左、右两边对称分布着2列气垫,其中每列有14块气垫,共28块气垫。

1.1.1 气浮悬架模型

真空管道车辆共有28块气动悬浮装置,首先选取单气浮垫车模型作为研究对象,将车辆与气浮垫看成是弹簧和阻尼并联的一系悬挂系统。一系气动悬挂装置的物理模型如图2所示。

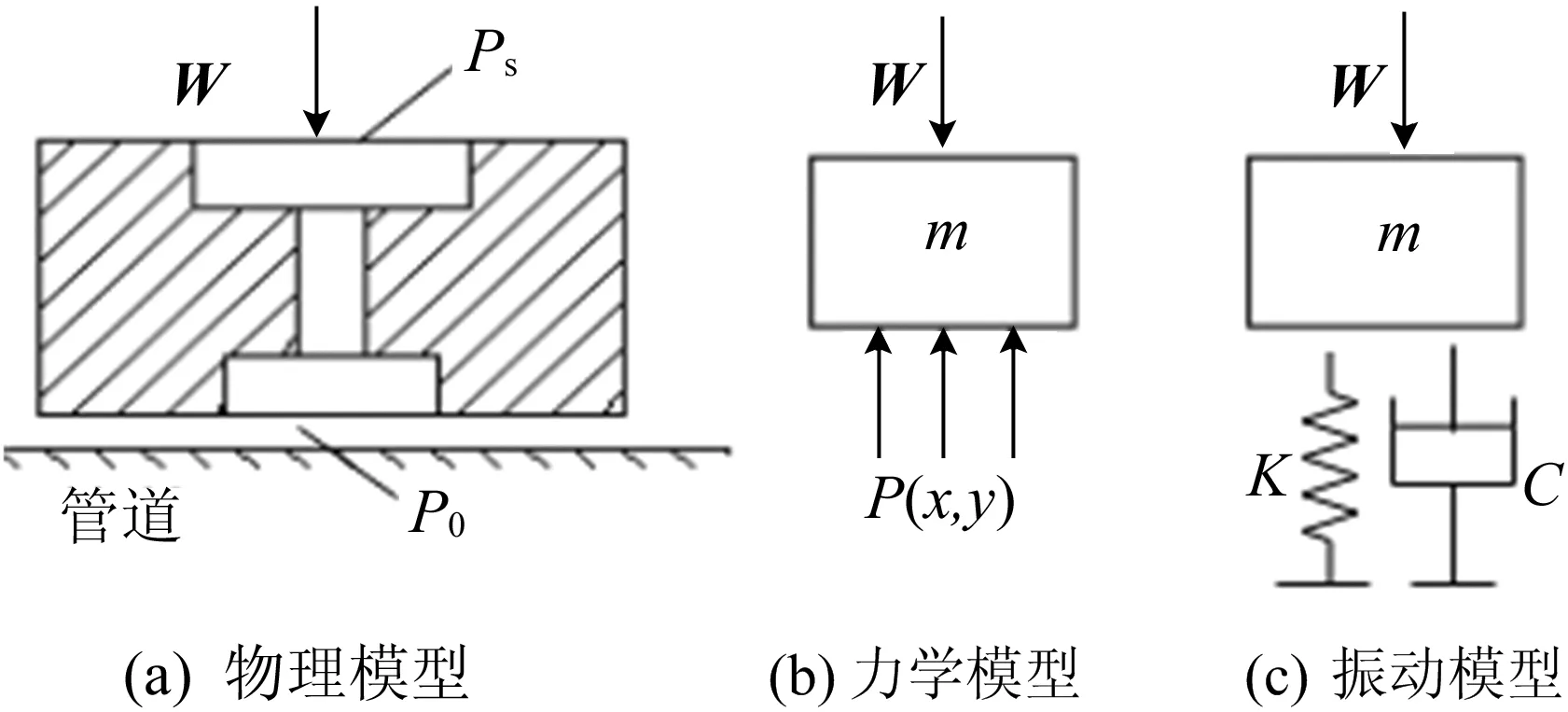
图2 气动悬浮装置物理模型

气动悬浮装置与管道之间的气膜本身具有一定的刚度K1,考虑到气体具有一定的黏性,可认为气浮垫在承载方向上具有阻尼C1。刚度K1、阻尼C1都是与气膜间隙h相关的函数[5]。一系气动悬挂系统的运动方程如下:

(1)

气动悬浮装置具有高刚度、低阻尼的特点,具有极差的垂向稳定性,因此必须在气动悬浮装置和车身间增加二系悬挂系统,以增加车辆垂向稳定性。车体和气动悬浮装置之间的连接视为无质量的二系悬挂链接,带有二系悬挂的单块气动悬浮装置的质量处理模型[6]如图3所示。

图3 带二系悬挂的模型

设二系悬挂刚度、阻尼分别为K2、C2,x1为气动悬浮装置的位移；x2为车体位移。增加二系悬挂后系统的微分方程为:

(2)

1.1.2 管道车辆模型

将车辆视为多刚体组成的动力系统,质量集中在车体上,车辆和管道之间的刚度和阻尼由弹簧和阻尼器来模拟。车辆包括车体的沉浮、点头2个运动[7]。

真空管道车辆与管道、支撑梁垂向耦合模型如图4所示。模型数学符号的物理意义为:ms为车体质量;Js为车体点头惯量;αs为车体点头角;Ks为二系悬挂刚度;Cs为二系悬挂阻尼;ybi为前(后)车体等效气浮垫垂向位移;Sbi为前(后)车体等效气浮垫到车体重心距离;Kbi为前(后)车体等效间隙刚度;Cbi为前(后)车体等效间隙阻尼。

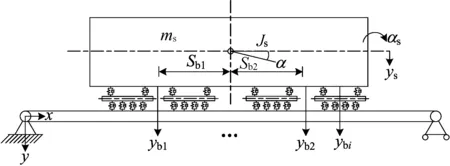
图4 真空管道车辆与管道、支撑梁垂向耦合模型

假设车辆坐标系以图4所示方向为正方向；车体、车架均视为刚体,不考虑各部件的变形;弹簧和阻尼均为线性;车辆各部件在各自平衡位置附近做小位移的振动。对车辆各部件进行受力分析[8-9],由牛顿第二定律可得车辆系统的动力学方程。

车体垂向运动平衡方程为:

(3)

车体点头运动平衡方程为:

(4)

其中,ysui为第i个二系悬挂上端垂向位移;ysbi为第i个二系悬挂下端垂向位移;Lsi为第i个二系悬挂点对车体点头运动的力臂。

对(1)式、(2)式进行整理并写成矩阵方程的形式，即

(5)

其中,Mc为车辆的质量矩阵;Cc为车辆的阻尼矩阵;Kc为车辆的刚度矩阵;Fc为车辆运动方程的荷载项；Zc为车辆的垂向位移矩阵。

1.2 管道-支撑梁运动平衡方程

管道-支撑梁是多自由度体系,其运动平衡方程为:

(6)

其中,Mb为支撑梁的质量矩阵;Cb为支撑梁的阻尼矩阵;Kb为支撑梁的刚度矩阵;Fb为支撑梁运动方程的荷载项。

根据真空管道车辆与管道-支撑梁的垂向耦合模型,分别取前、后气浮悬架的中心作为研究对象[10],得到车辆对管道-支撑梁作用的荷载为:

(7)

(8)

(9)

2 垂向动力学性能分析

2.1 带二系悬挂的车身垂向加速度分析

设一系悬挂的刚度和阻尼分别为K1、C1,由管道和支撑梁建造误差等引起的管道不平顺和车体位移分别为x0、x2,二系悬挂刚度和阻尼分别为K2、C2；G0=5.0×10-6m3/s,u=139 m/s,f0=0.1 Hz。x0由白噪声积分器产生,即

(10)

结合(1)式,利用Matlab/Simulink模块建立单块气动悬浮装置的动力学仿真模型[11-12],如图5所示。

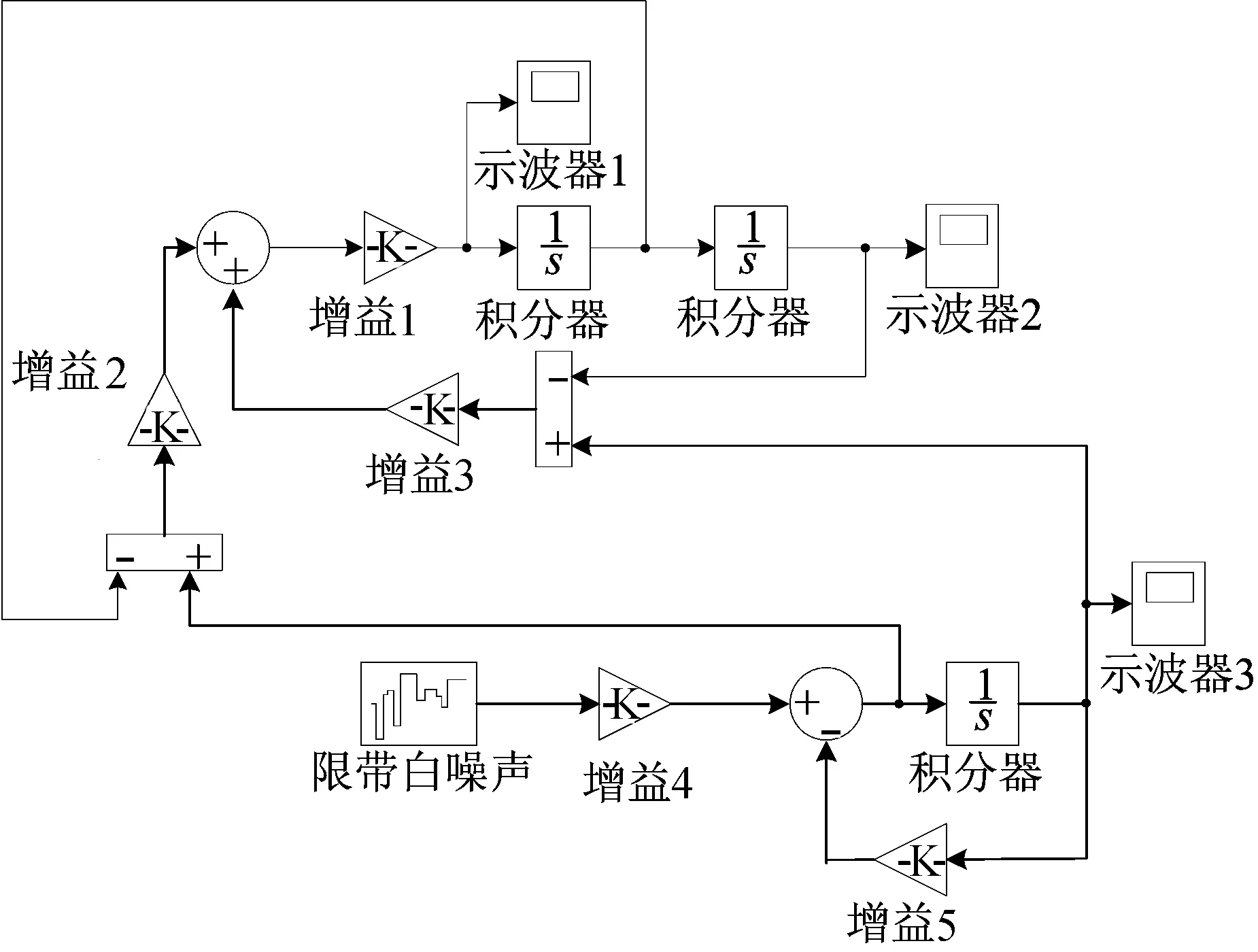
图5 悬架动力学仿真模型

设置模型的采样时间为0.025 s,采用固定步长方式,取K1=1.338×106N/cm,C1=6.692×104N·s/cm,K2=1×104N/cm,C2=1 000 N·s/cm,仿真时间为18 s。

仿真后得出原车车身的垂向加速度,如图6所示。

图6 一系悬挂车身垂向加速度

建立带二系悬挂的车辆的动力学仿真模型,如图7所示,带二系悬挂的车身加速度曲线如图8所示。

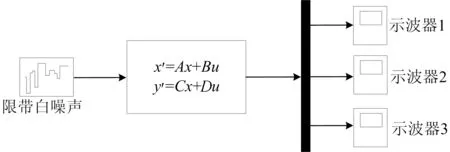
图7 带二系悬挂的车辆仿真模型

图8 带二系悬挂的车身加速度

由图6、图8可知,当车身不增加二系悬挂时,车身垂向加速度过高,不满足车辆垂向动力学性能以及舒适性要求。因此必须在车体和悬浮系统之间增加二系悬挂。

2.2 真空管道车辆耦合系统的计算方法

车辆管道-支撑梁耦合振动的分析方法可以分为时域法和频域法,本文采用时域法[13-14]进行分析。

(1) 将车辆模型与管道-支撑梁模型的所有自由度通过气膜间隙耦合在一起,消除不独立自由度,建立统一的系统运动方程组进行同步求解。

(2) 以气膜间隙为界,将真空管道车辆分为车与管道-支撑梁2个子系统,分别建立运动学方程。两者之间通过气膜间隙处的位移协调条件与相互作用力的平衡关系解耦平衡运动方程。

从计算车桥耦合振动的数值分析方法中选取常用的精度较高且计算速度较快的Newmark法,结合它的计算特点编制Matlab计算程序,并通过算例进行结果比较。

Newmark法是结构动力分析中最常用的计算方法之一,1959年英国人Newmark基于以下公式发展了一类时间步进法,即

(11)

(12)

(1) 初始计算,即

选择Δt,可得:

(2) 对每个时间步i进行计算,即

将车体和管道-支撑梁以气膜间隙为界分为2个子系统,分别建立车辆和管道-支撑梁的运动方程和2个系统之间在气膜间隙处满足位移协调条件与相互作用力的平衡关系,最后采用迭代法求解系统响应。基于Matlab平台,采用Newmark法进行耦合数值计算分析,具体求解思路与过程如下:

(1) 在t时刻,提取当前管道-支撑梁的动力响应作为初始迭代值,并以此为基础通过插值计算车辆轮对处响应的位移、速度和加速度。

(2) 根据求得的车辆轮对处响应的位移、速度求解车辆受到的力的作用,并利用Newmark法计算t+dt时刻车辆的动力响应。

(3) 根据轮对响应的位移、速度、加速度和t+dt时刻车辆的动力响应,计算车辆对管道-支撑梁的作用力。

(4) 根据t时刻的支撑梁响应，采用Newmark法计算t+dt时刻的管道-支撑梁动力响应。

(5) 重复步骤(1)～ 步骤(4),直至2次相邻计算的管道-支撑梁响应收敛,再进行下一个时间步计算。

步骤(5)中先根据前、后相邻2次计算得到同一时刻的车辆、管道-支撑梁响应的差值向量,然后计算其向量的范数作为收敛性判断的依据[15-16]。步骤(5)的收敛性判断是必要且关键的,这将在后面的计算中得到证明。

2.3 垂向动力学分析

对所建立的车辆与管道-支撑梁振动模型和磁悬浮车辆进行动力学分析。Hyperloop真空管道车辆和TR06磁悬浮车辆参数[17-18]见表1所列,Hyperloop管道-支撑梁和Emsland磁浮线路高架梁参数见表2所列。

表1 Hyperloop真空管道车辆和TR06磁悬浮车辆参数

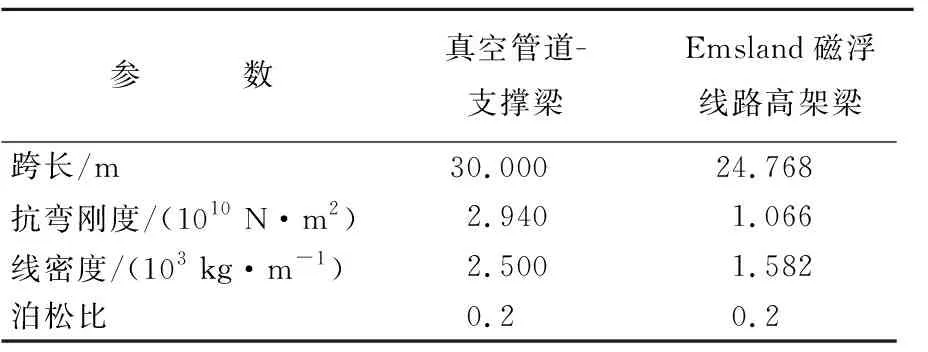
表2 Hyperloop管道-支撑梁和Emsland磁浮线路高架梁参数

为了对比真空管道车辆与磁悬浮车辆在高速和超高速域的过桥管道动力特性,选取真空管道车辆的管道-支撑梁与磁悬浮车辆的桥梁进行分析。计算参数模态阻尼比ζ=0.1,时间积分步长为 0.01 s。

真空管道车辆和磁悬浮车辆以500 km/h的速度通过跨度为30 m管道或桥梁时,车桥系统典型动力学响应时程曲线如图9所示。

由图9a可知,在车速达到500 km/h时,真空管道车辆所引起的管道-支撑梁振动加速度只有0.4 m/s2左右,小于管道-支撑梁竖向振动加速度限值0.35g[19],其振动加速度也小于磁悬浮车辆对管道-支撑梁产生的振动加速度;由图9b、图9c可知,真空管道车辆通过管道时产生的车体振动加速度及相应的管道-支撑梁跨中挠度均小于磁悬浮车辆。

图9 车桥系统动力响应时程曲线

真空管道车辆和磁悬浮车辆以不同速度通过跨度为30 m管道或桥梁时,车桥系统动力学响应曲线如图10所示。

由图10a、图10b可知,真空管道车辆通过管道时,管道振动加速度均小于磁悬浮车辆;在行车速度低于500 km/h时,车体振动加速度和真空管道车辆引起的管道-支撑梁挠度略大于磁悬浮车辆,但相差很小;在速度高于500 km/h时,车体振动加速度和真空管道车辆引起的管道-支撑梁挠度小于磁悬浮车辆,且这种差异随着行车速度的提高而加大。真空管道车辆和磁悬浮车辆过桥时的振动响应在速度为500 km/h、车体垂向振动加速度为0.08 m/s2左右时远小于其舒适度限值0.125g[20]。总体而言,在超高速(速度大于500 km/h)运行条件下, 真空管道车辆所引起的管道垂向振动加速度仅为磁悬浮车辆的1/2。由图10c可知,对30 m跨度管道而言,2种车辆以100～700 km/h速度过桥所引起的支撑梁变形均远小于支撑梁挠跨比限值1/1 800。这表明真空管道车辆在超高速运行时仍具有良好的稳定性。

图10 不同车速时车桥系统动力响应曲线

3 结 论

真空管道车辆采用全管道支撑梁一体设计,其线路成本占总成本的70%～80%[12],因此,研究真空管道车辆车桥耦合动力作用规律显得极为重要。为了进一步优化车辆和管道支撑梁的动力学参数,降低线路成本,提高真空管道车辆的安全性和稳定性,必须充分认识真空管道车辆车桥耦合动力作用规律。本文以Hyplerloop真空管道车辆及其运行线路为对象,开展了真空管道车辆与管道桥梁的垂向耦合动力学研究,对比分析了磁悬浮车辆在两跨梁上的垂向动力学响应,得到如下结论:

(1) 真空管道车辆必须在车体和悬浮系统之间增加二系悬挂,才能满足车辆垂向动力学性能。

(2) 真空管道车辆的梁跨中挠度小于其相应的挠跨比限值,车体垂向加速度小于德国ICE高速车辆舒适度限值0.125g,车辆和管道的动力响应较小。

(3) 在管道具有高平顺性的前提下,车速低于500 km/h时,磁悬浮车辆的振动加速度和车辆引起的管道支撑梁挠度略小于真空管道列车,但相差不大；在车速高于500 km/h时,真空管道车辆各项垂向动力学参数优于磁悬浮车辆。

(4) 真空管道车辆和管道-支撑梁的相互作用方式与磁悬浮车辆对应的磁轨作用方式略有不同,但真空管道车辆的受力情况与磁悬浮车辆情况类似,都是非直接接触。两者均具有足够的强度与安全裕度,能很好地满足各自运用要求。从每米管道所受荷载来看,真空管道车辆与真磁悬浮车辆基本相当。