一类非二元循环码的重量分布

李 梦, 刘 丽, 谢贤红

(1.合肥工业大学 数学学院,安徽 合肥 230601; 2.中国科学技术大学 网络空间安全学院,安徽 合肥 230026)

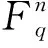
循环码是线性码的子类,具有有效的编码和解码算法特性,可以应用到消费电子产品,数据存储系统和通信系统中;同时,少重量的线性码在密钥共享方案[1]和认证码[2]中应用广泛。因此,研究线性码的重量分布理论具有重要的基础理论意义。

(1) 码的重量分布是计算错误检测和纠正概率的主要依据。

(2) 重量分布是研究码结构的主要工具,可以通过改进码字的内在关系寻找新的好码。

近年来,由于计算循环码的重量分布的困难性,只能得到少数满足特殊情况的循环码的重量分布。

文献[3]得到了2类循环码,可用于密钥共享方案,本文将进一步进行这方面的研究。

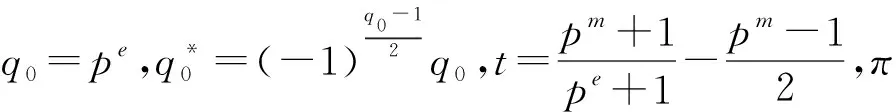
此时,p-分圆陪集Ct={t,tp,tp2,…,tpm-1}模q-1的阶等于m、π-1和π-t在Fp上的极小多项式的次数相同。定义循环码为:

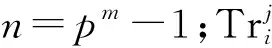
由Delsarte定理[4]可知,码C的维数为2m。码字c(α,β)=(c0,c1,…,cn-1)的Hamming重量为:

WH(c(α,β))=|{i|0≤i≤n-1,ci≠0}|=

(1)

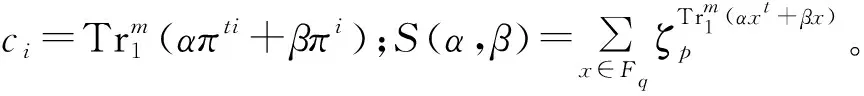
显然,可以通过计算指数和S(α,β)的值分布来确定循环码C的重量分布。当p≡3(mod 4)时,文献[5]计算出S(α,β)的值分布,从而确定了这类循环码的重量分布。本文将解决p≡1(mod 4)的情形,为此，以下总是假设p≡1(mod 4)。

本文确定了码C在e为奇数和偶数2种情况下的重量分布，并通过对码C的码字进行截断得到了另一类循环码。

1 预备知识

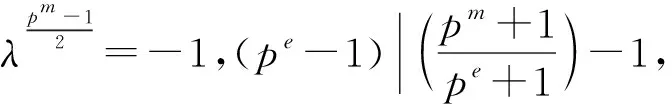
当e、m都为偶数时,任取Fp中的元素a,有at=a;当e,m都为奇数时,无法得出at=a。故对于Fp中的平方元a,可得at=a。

引理1 令F表示域Fq,则F2=Fpe+1,且F=Fpe+1∪λFpe+1。

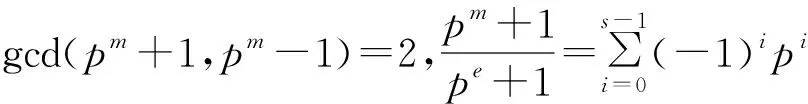
设x∈F,由xpm=x可得:

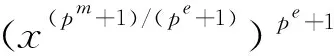
根据λ的性质,可得F=Fpe+1∪λFpe+1。

(2)

为了计算S(α,β)的值分布,需要确定指数和T(α,β),以下简要介绍有限域上的二次型的相关知识。

引理2[3]定义一个Fq到Fq0的函数:

则Q(α,β)(x)是Fq0上的二次型,且

其中,rα,β为Q(α,β)(x)的秩;ζp为p次本原单位根;η0为Fq0的二次乘法特征,即

(1)rα,β=s,s-1或s-2;

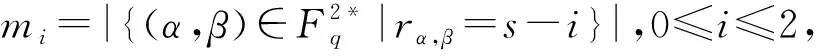
m1=(pm-1)pm-e,

m0=p2m-1-m1-m2。

结合引理2和引理3,定义以下2个常量:

对ν=±1,i∈{0,1,2},假设

mν,i=|Vν,i|,则Vi=V-1,i+V1,i且mi=m1,i+m-1,i。

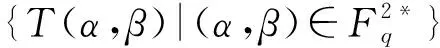
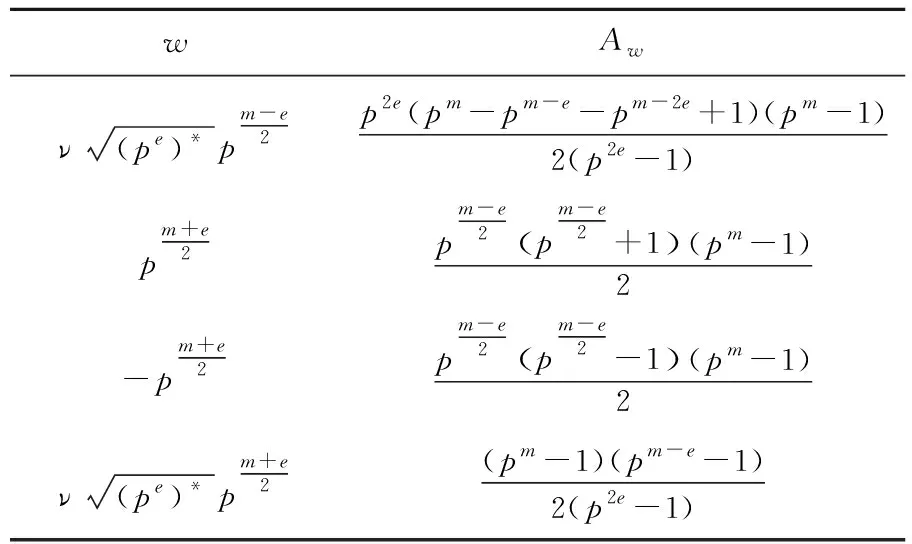
表1 m/e为奇数,ν=±1时T(α,β)的值分布

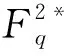
最后介绍分圆域Q(ζp)的伽罗瓦群的性质。

2 循环码C的重量分布

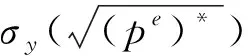
2.1 e为奇数时C的重量分布

表2 e、m/e为奇数时循环码C的重量分布

证明由引理6及(1)式、(2)式可知:

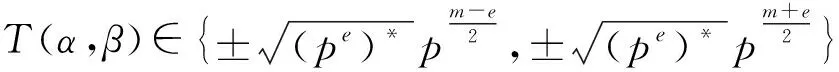
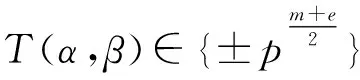
结合引理4和引理5得循环码C的重量分布。

以下推论仅给出e是奇数时码C的性质。

推论1 设wmax和wmin分别表示码C的极大重量和极小重量,则有:

故码C可用于构造密钥共享方案和认证码[1]。

例1 令p=5,m=3,e=1,C是F5上[124,6,90]循环码,经计算得其重量计数器为:

1+3 270x90+9 424x100+2 480x110。

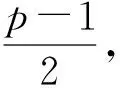
C′={c′(α,β)|α,β∈Fq}。

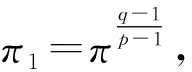
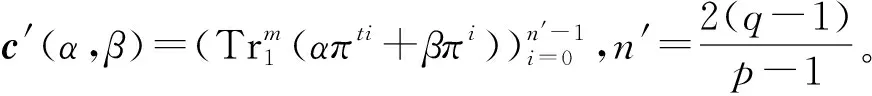
表3 e、m/e均为奇数时线性码C′的重量分布

例2令p=5,m=3,e=1,则C′是F5上[62,6,45]线性码,经计算得其重量计数器为:

1+3 270x45+9 424x50+2 480x55。

2.2 e为偶数时C的重量分布

下面利用文献[9]中的方法给出S(α,β)满足的恒等式。观察可得:

其中

由t是奇数可得(-1)t=-1,因此Ω1=pm。同时,

其中,Ω2表示下列方程组

(3)

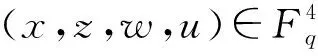
引理7 令e为偶数,则下列等式成立:

(4)

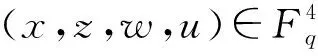
(5)

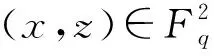
且

(1) 若b1为平方元,则

T2(a1,b1)=

(2) 若b1为非平方元,则

T2(a1,b1)=

证明证明分成以下几种情况:

(1)a1=b1=0时,T2(0,0)=Ω1。

(2)a1≠0,b1=0时，由(6)式中的第2个等式可得x=-z,从而有a1=0,产生矛盾,因此T2(a1,0)=0。

(3)a1≠0,b1≠0时，实际上,这种情况很难直接计算,但可以根据(5)式中x与z的平方性分为以下4种情况来讨论:

情况1x与z皆为平方元;

情况2x和z皆为非平方元或0;

情况3x为平方元,z为非平方元;

情况4x为非平方元,z为平方元。

现依次讨论每个情况对应T2(a1,b1)的值。

情况1x与z皆为平方元。

(6)

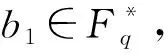
(1) 若b1是一个平方元,则

T2′=

(2) 若b1是一个非平方元,则

T2′=

证明设(x1,z1)为(6)式中第2个方程的解,显然x1≠z1,不妨假设:

(7)

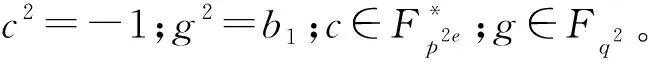
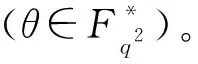
(8)

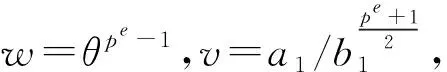
w2-2vw+1=0

(9)

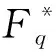
(10)

则(6)式可整理为:

(11)

即T2′为(11)式的解。

接下来，讨论T2′的值。

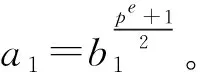
(12)

(13)

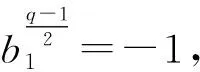
(14)

(15)

令Γ1和Γ2分别表示(14)式和(15)式关于θ在Fq2中的解集；显然Γ1∩Γ2=∅，且(11)式的解集等于Γ1∪Γ2。易见θ是(14)式的解当且仅当θ-1是(15)的解,故|Γ1|=|Γ2|,且(9)式的非零解成对出现。

当(11)式有解时,求|Γ1|。设θ1、θ2为(14)式的2个非零解,则

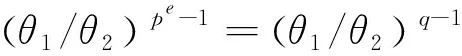
因为gcd(pe-1,q-1)=pe-1,|Γ1|=pe-1,所以(11)式关于θ在Fq2中有2(pe-1)个非零解。

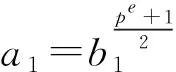
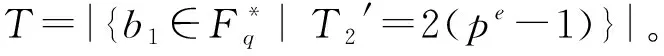
若T2′=2(pe-1),则可得:

(pe-1)+2(pe-1)T=q-1。

类似可得b1是非平方元的结论。

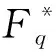
(1) 若b1是一个平方元,则

T2″=

(2) 若b1是一个非平方元,则

T2″=

证明以下考虑(6)式解的情况。若(x1,z1)是(6)式的解,则(-x1,z1)、(-x1,-z1)及(x1,-z1)也是(6)式的解。

若x1z1≠0,则(6)式恰有4个不同的解,但只作为(5)式的1个解存在。

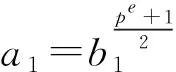
T2″=T2′=

情况2x和z皆为非平方元或0。

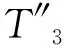
(1) 若b1是一个平方元,则

T3″=

(2) 若b1是一个非平方元,则

T3″=

证明该证明与情况1的证明类似,此处省略。

情况3x为平方元,z为非平方元。

(16)

引理12 令T4′表示(16)式解的个数,则

T4′=

证明设(x1,z1)为(16)式中第2个方程的解,显然x1≠z1,不妨假设

(17)

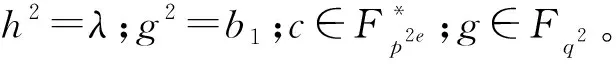
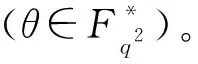
以下证明步骤与引理9类似,此处省略。

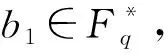
T4″=

证明考虑(16)式解的情况。若(x1,z1)是(16)式的解,则(-x1,z1),(-x1,-z1)及(x1,-z1)也是(16)式的解。

若x1z1≠0,则(15)式恰有4个不同的解,但只作为(5)式的1个解存在。

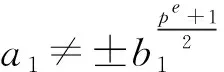
T4″=T4′=

情况4x为非平方元,z为平方元。

引理14 令T5″表示(5)式关于(x,z)的解的个数(其中,z是一个平方元、x是一个非平方元或x=0),则

T5″=

证明情况4与情况3对称,证明略。

由引理10、引理11、引理13和引理14可得引理8。

表5 e为偶数、m/e为奇数,ν=±1时循环码C的重量分布

证明首先计算指数和S(α,β)的重量分布。

对ν,μ=±1,0≤i,j≤2,定义以下常量:

Vν,μ,i,j={(α,β)|(α,β)∈Vν,i,

(-λα,λβ)∈Vμ,j},

mν,μ,i,j=|Vν,μ,i,j|。

由引理5的证明可知,当i、j非零时,mν,μ,i,j=0。由T(α,β)和T(-λα,λβ)的对称性可知mν,μ,i,j=mμ,ν,j,i,因此只需计算mν,μ,i,:=mν,μ,i,0即可。

由引理3和引理4,有

m1,1,0+m-1,1,0+m1,1,1+m-1,1,1+

m1,1,2+m-1,1,2=m1,0

(18)

m1,-1,0+m-1,-1,0+m1,-1,1+m-1,-1,1+

m1,-1,2+m-1,-1,2=m-1,0

(19)

结合(2)式和引理3,有

m1,1,1+m1,-1,1=m1,1

(20)

m-1,1,1+m-1,-1,1=m-1,1

(21)

m1,1,2+m1,-1,2=m1,2

(22)

m-1,1,2+m-1,-1,2=m-1,2

(23)

T(λα,λβ)=η0(λ)rα,βT(α,β)。

对奇数s,当rα,β=s或s-2,η0(λ)=-1时,

T(λα,λβ)=-T(α,β)

(24)

由(24)式知,存在一个一一映射，即

V-1,1,1,0→V-1,-1,1,0,

由此可得m-1,1,1=m-1,-1,1。

类似可得下列等式成立,

m1,1,1=m1,-1,1,m1,1,2=m-1,-1,2,

m-1,1,2=m1,-1,2,m1,1,0=m-1,-1,0,

m1,-1,0=m-1,1,0。

结合引理7、(10)～(15)式、(20)式及(21)式,易得:

(2m1,-1,2+2m-1,1,2)+p4m=

求解由(10)～(17)式、(18)式及(20)～(23)式构成的方程组,可得到S(α,β)的值分布。

WH(c(α,β))=pm-1(p-1)-

其中,ν,μ∈{±1};0≤i,j≤2。由此可得e为偶数时循环码C的重量分布。

例3 令p=5,m=6,e=2,C是F5上[15 624,12,11 300]循环码,得其重量计数器为:

1+5 077 800x12 200+5 077 800x12 300+

4 687 200x12 700+4 687 200x12 800+

15 624x11 300+15 624x13 700+

56 340 144x12 400+56 340 144x12 600+

111 899 088x12 500。

在偶数的情况下,表5中码C中的所有非零码字都有公因子p-1,可以推导出πn′t=πn′=π1,这意味着码C的任何码字c(α,β)都可以用c′(α,β)表示:

WH(c′(α,β))=WH(c(α,β))/(p-1)。

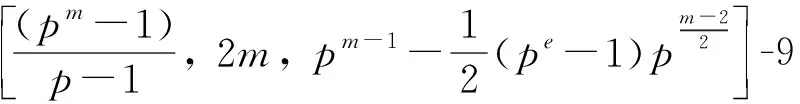
表6 e为偶数、m/e为奇数,ν=±1时线性码C′的重量分布

表6中w为C′中码字的重量；Aw为C′中重量为w的码字个数。

例4令p=5,m=6,e=2,C′是F5上[3 906,122 825]线性码,计算得重量计数器为:

1+5 077 800x3 050+5 077 800x3 076+

4 687 200x3 175+4 687 200x3 200+15 624x2 825。

3 结 论

本文给出了一类对偶码含2个重点的非二元循环码的重量分布，并利用magma程序验证了结果的正确性。可以看出，得到的线性码为少重量的，可应用于密钥共享方案。进一步的研究将会寻找更一般的函数，从而构造出性能更好的线性码，并给出一般表达式。