电渣重熔Mn18Cr18N钢的热变形行为与本构方程
2020-11-04张学瑞秦凤明何文武陈慧琴
张学瑞,秦凤明,何文武,陈慧琴
(太原科技大学 材料科学与工程学院,太原 030024)
Mn18Cr18N高氮奥氏体不锈钢因具有高强高韧以及良好的抗应力腐蚀性能被广泛应用于发电机护环的生产[1]。鉴于电渣重溶钢锭纯净度和致密度高的优良品质,目前均采用Mn18Cr18N电渣重熔钢锭进行大型发电机护环的生产制造。但是由于电渣重溶过程中钢锭的特殊冷却条件,一般电渣重熔钢锭均具有粗大的柱状晶组织,从而导致电渣重熔钢锭的热塑性差,热加工温度区间窄,容易产生微观裂纹和粗晶、混晶等问题[2-4]。所以,Mn18Cr18N电渣重熔钢锭锻造的关键是细匀化晶粒组织[5-6]。
Mn18Cr18N奥氏体不锈钢具有较低的层错能[7],热变形过程中将发生动态回复或动态再结晶,从而使流变应力曲线呈现动态回复型曲线和动态再结晶型曲线。其中,动态再结晶在降低材料流动应力方面有着重要作用,能够改善材料的热加工性能。季长涛[8]等人对0Cr18Mn18N0.6奥氏体不锈钢热轧板进行了不同变形量的塑性变形,并对塑性变形及再结晶前后的组织进行了分析。Fengming Qin[9-10]等对铸态的Mn18Cr18N奥氏体不锈钢在不同的变形参数下进行热压缩实验,得到了其本构方程,并分析讨论了位错和孪晶两种动态再结晶机制。Z.Yanushkevich[11]等的研究表明奥氏体不锈钢的微观组织演变机理是由变形位错控制的不连续动态再结晶。
本文通过实验方法确定了变形温度和应变速率对流动应力以及微观组织的影响,并采用两段式流动应力模型构建了电渣重熔Mn18Cr18N钢的热变形本构方程,分析了动态再结晶微观组织演变规律,构建了动态再结晶的体积分数模型,可为电渣重熔Mn18Cr18N钢热加工工艺提供理论依据。
1 试样制备与实验方法
采用的实验材料为电渣重熔Mn18Cr18N护环钢(ESR Mn18Cr18N),其化学成分见表1.在Gleeble-1 500D热模拟试验机上进行单向压缩试验,试样尺寸为Φ8×12 mm.材料的原始微观组织结构如图1所示。热压缩实验中,试样以10 ℃/s加热到1 200 ℃并保温120 s,然后以10 ℃/s降温到不同变形温度(950 ℃,1 000 ℃,1 050 ℃,1 100 ℃,1 150 ℃)保温120 s以消除试样内部的温度梯度。应变速率为0.001~1 s-1,真应变为0.69,试样在热变形结束后迅速水淬以保留其高温变形后的组织状态。热变形后的试样沿轴向切开,经过金相样品的制备流程后在OLYMPUS-PMG3金相显微镜下进行组织观察,腐蚀剂为1 mLHF、1.5 mLHCl、2.5 mLHNO3和95 mLH2O组成的混合液体[12]。
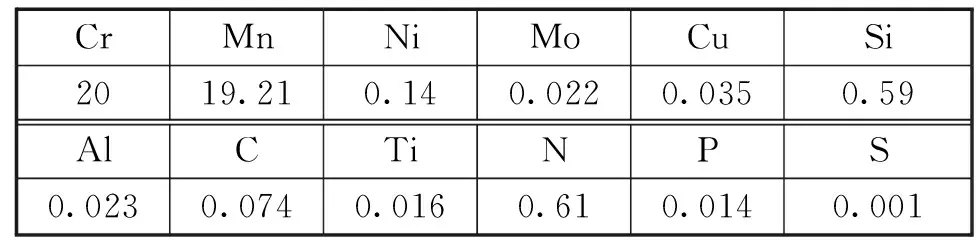
表1 Mn18Cr18N钢的化学成分(wt%,质量分数)Tab.1 Chemical composition of Mn18Cr18N steel (wt%,mass fraction)
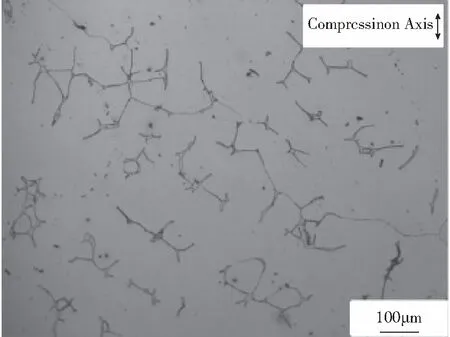
图1 ESR Mn18Cr18N奥氏体不锈钢原始微观组织Fig.1 The original structure in ESR Mn18Cr18N austenitic stainless steel
2 结果与讨论
2.1 应力-应变曲线
图2为ESR Mn18Cr18N护环钢在不同应变速率和变形温度下的应力-应变曲线。可以看出,在不同的变形参数条件下,该钢的热变形流变应力曲线均呈现动态软化型曲线特征,其峰值应力、峰值应变等特征值随着变形温度的降低以及应变速率的升高而出现增大的趋势。0.001~0.1 s-1的应变速率范围内,峰值应力随应变速率的升高显著增大;0.1 s-1和1 s-1的应变速率范围内,峰值应力随应变速率的升高略有增大。如变形温度1 000 ℃时,0.001 s-1、0.01 s-1、0.1 s-1、1 s-1条件下峰值应力分别为101 MPa、134 MPa、182 MPa、199 MPa.950 ℃~1 100 ℃之间,峰值应力随温度的升高急剧降低;1 100 ℃~1 200 ℃之间,峰值应力随温度的升高逐渐降低。如应变速率0.1 s-1时,950 ℃、1 000 ℃、1 050 ℃、1 100 ℃、1 200 ℃条件下峰值应力分别为232 MPa、182 MPa、136 MPa、115 MPa、53 MPa.金属的热变形过程就是动态软化和加工硬化相互作用的过程。其中,动态软化机制主要包括动态再结晶与动态回复。动态回复过程中主要是位错的交滑移和攀移,而动态再结晶主要是高位错密度驱动下晶核的形核和长大过程,从而使位错密度降低;加工硬化则主要由位错的增殖和位错间的相互作用等现象而使位错累积产生的。变形温度的升高为位错的交滑移和攀移提供了驱动力,增大动态回复以及动态再结晶的软化能力;应变速率增大时,在同一变形量下的变形时间减少,动态再结晶的软化机制不能得到充分的进行。所以,如图2所示,较高的变形温度和较低的应变速率情况下易发生动态再结晶行为。

图2 ESR Mn18Cr18N 护环钢不同应变速率下的真应力-应变曲线Fig.2 True stress-strain curves of ESR Mn18Cr18N retaining ring steel at different strain rates
2.2 热变形微观组织
图3为ESR Mn18Cr18N奥氏体不锈钢热变形过程中动态再结晶组织。相同温度条件下(图3(a)、(b)),随着应变速率的增大,动态再结晶百分数降低,动态再结晶晶粒尺寸没有明显变化。表明ESR Mn18Cr18N奥氏体不锈钢的热变形过程对应变速率较为敏感。

图3 不同变形条件下的微观组织Fig.3 Microstructures under different deformation conditions(ε=0.693)
相同应变速率条件下(图3(c)、(d)),随着变形温度的升高,原子的扩散能力提升,提供给动态再结晶形核需要的能量也增多,从金相组织上可以观察得到动态再结晶晶粒尺寸增大,动态再结晶百分数也提高。所以,ESR Mn18Cr18N奥氏体不锈钢热变形过程中变形温度的提高对动态再结晶会有促进作用。
2.3 热变形特征参数
金属的高温塑性变形过程是一个热激活过程。通常情况下,用温度补偿应变速率参数,即Z参数来表征变形温度和应变速率对动态再结晶的综合影响。如式(1)所示。
(1)
式中:Q:热变形激活能(kJ/mol);
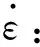
R:气体常数,R=8.314 41 J/(mol·k);
T:绝对温度(K);σ:流变应力(MPa);
A1、A2、A、α、β为材料的常数。


图4 峰值应力和应变速率的关系Fig.4 The relation of peak strain and strain
对式(1)两边同时取对数得式(2).
(2)

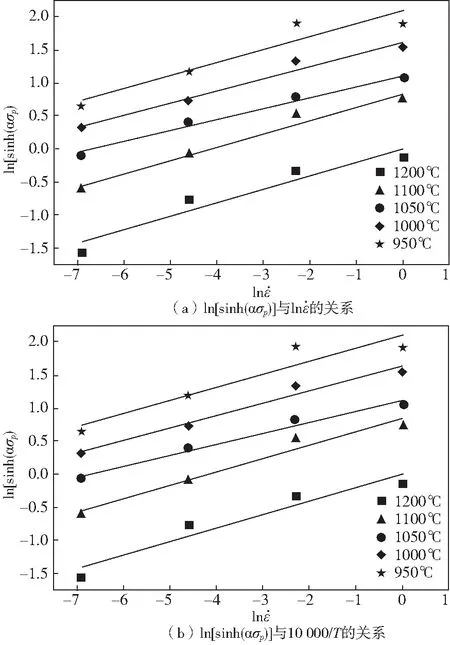
图5 峰值应力与应变和温度的关系Fig.5 The relation of peak stress with strain rate and temperature
根据方程(2),可以得到lnZ和ln[sinh(ασp)]的关系,从而得到Z与σp之间的关系。根据lnZ和ln[sinh(ασp)]的关系曲线,得到A的平均值A=1.96×1023.从而能得到式(1)中的双曲正弦函数表达式(3).
(3)
2.4 基于动态软化曲线特征点的两段式本构方程的建立
由图2看出,Mn18Cr18N钢在实验参数条件下的热变形流动应变曲线由峰值应变前的硬化曲线和峰值应变后的动态再结晶软化曲线组成,因此,本文采用两段式Laasraoui方程建立该钢的热变形流动应力方程(本构方程),如式(4)所示。
(4)
式中:σWH为加工硬化阶段应力的外延值;σ0初始应力;σs饱和应力;σss稳态应力;σc动态再结晶临界应变;Kd,nd,K2均为常数。
2.4.1 特征应力参数的确定
根据文献[17],使用Z参数的函数来定义初始应力σ0,如式(5)所示:
σ0=pZq
(5)
式中:q为材料常数。根据实验数据,通过线性回归得到初始应力的表达式为:
σ0=0.132Z0.078
(6)
稳态应力σss和饱和应力σs同样可以由Z参数的函数来定义:
Z=Ass[sinh(ασss)]nss
(7)
Z=As[sinh(ασs)]ns
(8)
Ass、nss、AS、ns为常数,ln(sinh(ασss)-lnZ和ln(sinh(ασs)-lnZ的关系分别由图6(a)、6(b)表示,通过线性回归分别得到稳态应力σss和饱和应力σs的表达式为:

图6 稳态应力和饱和应力与Z参数的关系Fig.6 The relations of the steady stress and saturated stress with Z parameter
σss=83.33sinh-1(105 820Z)4.55
(9)
σs=83.33sinh-1(17 667.84Z)5.26
(10)
将初始应力、饱和应力以及在加工硬化阶段时不同变形条件下的应力σ、应变ε代入到方程(4)中,可以计算出K2:
K2=uZv
(11)
u、v为常数。通过对lnK2与lnZ之间做线性回归,能够得到K2关于Z的函数表达式为:
K2=4.2×10-6Z-0.045
(12)
2.4.2 动态再结晶临界应变的确定
动态再结晶临界应变是表征动态再结晶起始的特征应变,一般略小于峰值应变。通常根据硬化率θ与应力σ的关系曲线,即加工硬化率曲线(θ-σ曲线)特征点确定[18]。如图7所示的θ-σ曲线,临界应变则对应于曲线上的切点σc.同样,峰值应变、稳态应变和饱和应变也可在图7中的加工硬化率曲线特征点处确定。
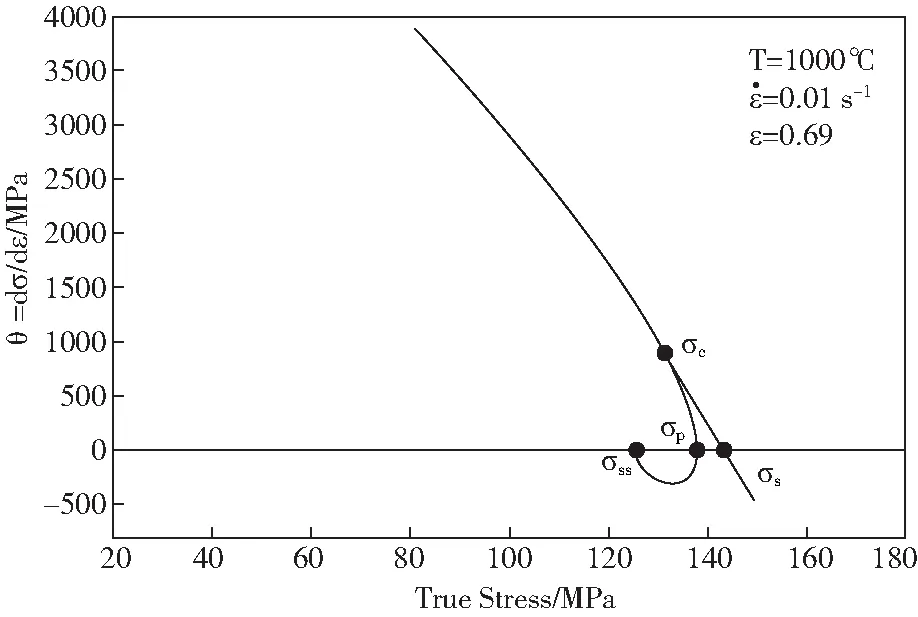
图7 在温度1 000 ℃,应变速率0.01 s-1时θ-σ曲线Fig.7 The θ-σ curve at 1 000 ℃ and strain rate 0.01 s-1
特征应变同样可以由Z参数表示。通过加工硬化率曲线和实验数据分析,获得峰值应变模型为:
εp=9.93×10-6Z0.165
(13)
通过对θ-σ曲线的读取,找到临界应变εc和峰值应变εp之间的关系有:
εc=0.83εp
(14)
2.4.3 动态软化方程
由式(13)-(14)可知,临界应变随着Z参数的增大而增加,即高温低应变速率下(Z参数减小)临界应变较低,动态再结晶更容易发生。在应变低于临界应变时,加工硬化处于主导地位,未发生动态再结晶。当应变超过临界应变时,位错密度和畸变能随着变形应变的增加而增大,开始发生动态再结晶;当应变超过峰值应变时,应力软化占主导作用;随着应变的增大,再结晶分数增加,应力不断软化,直到应力达到稳定状态。在稳态变形过程中,随着应变的增加,加工硬化与动态软化达到了动态平衡,此时动态再结晶过程结束。
动态再结晶分数与应力(应变)的关系由方程(15)表达:
(15)
为了得到常数kd和nd,把方程(15)变形,两端分别取对数,得到方程(16)
(16)
对方程(16)中已确定的值进行线性回归分析,得到图8,ln(-ln(1-Xdrx))与ln((ε-εc)/εp)的关系曲线。
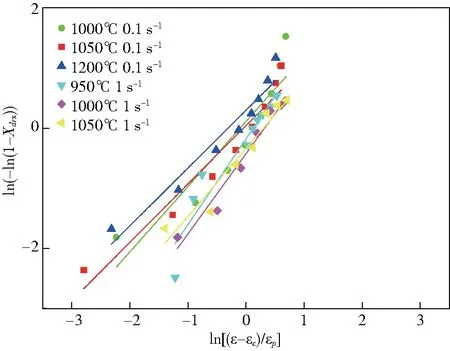
图8 ln(-ln(1-Xdrx))与的关系Fig.8 The relation of ln(-ln(1-Xdrx)) and
通过上图,把得到的nd、kd取平均值,得到nd=0.37,kd=0.535.因此,试验钢的动态再结晶分数模型由方程(17)表示:
(ε>εc)
(17)
根据以上分析,获得实验钢的高温流动应力模型:
(18)
式中:σ0=0.132Z0.078,K2=4.2×10-6Z-0.045,εp=9.93×10-6Z0.165,εc=0.83εp,σss=83.33sinh-1(105 820Z)4.55,σs=83.33sinh-1(17 667.84Z)5.26.
3 结论
通过Mn18Cr18N护环钢在变形温度为950 ℃~1 200 ℃和应变速率为0.001 s-1~1 s-1热变形行为研究,获得以下结论:
(1)Mn18Cr18N钢的热变形应力-应变曲线具有动态软化曲线特征,热变形激活能为637.351 kJ/mol,高于锻态材料的激活能;应变指数为4.95,说明实验材料在热变形过程中的流动应力由位错攀移所控制。
(2)建立了基于动态软化曲线特征点的Mn 18Cr18N钢的热变形两段式本构方程:
式中:σ0=0.132Z0.078,K2=4.2×10-6Z-0.045,εp=9.93×10-6Z0.165,εc=0.83εp,σss=83.33sinh-1(105 820Z)4.55,σs=83.33sinh-1(17 667.84Z)5.26.
