一种基于Spark的高效增量频繁模式挖掘算法

荀亚玲，孙娇娇，毕慧敏

(太原科技大学计算机科学与技术学院，太原030024)

频繁项集挖掘(FIM)是一项非常重要的数据挖掘任务，其主要任务是查找交易数据库中经常一起出现的项目集、序列或子结构[1]。 FIM已经引起了数据挖掘领域和各种实际应用领域的广泛关注[2-3]。但是，其挖掘过程占用大量CPU和I/O，因为会生成大量中间项和结果项集，并且此过程中涉及的数据集也很大。

本文采用一种无损树结构(FCFP-Tree)[4]，通过在维护与新增数据相对应的树结构时避免重新扫描原始数据集，以显著减少I/O.为了突破单机资源进行大数据处理的限制，开发了一种基于内存计算Spark平台的分布式解决方案，该解决方案设计了更为合理的RDD转换策略并采用相关组投影技术来优化通信和计算开销。

1 相关研究

关联规则挖掘一直以来都是数据挖掘研究的热点课题，由于数据集往往随着时间的变化而不断积累，因此，原先的挖掘结果可能已不适用，为了有效挖掘新的模式，增量挖掘算法被广泛研究。增量挖掘算法大致可分为三类：(1)基于Apriori的增量挖掘：如早期的FUP算法和相应的改进算法FUP2算法[5]，它们仍继承了Apriori的固有缺点，即需要多次扫描原始数据集；TDUP算法亦是基于Apriori的增量挖掘算法[6]，先利用Apriori算法从初始数据集中提取正区域和边界区域中的项目集，而后根据增量数据更新项目集的支持计数，仅考虑和计算边界区域中的那些项集，由于不考虑负区域的项目集，因此TDUP可能会错过一些具有增量数据更新的潜在频繁项目集；(2)基于分区的增量挖掘：为了避免类-Apriori算法需多次扫描数据库并生成大量候选集的问题，一种基于分区的滑动窗口过滤(SWF)算法被提出[7]，其基本思想是将事务数据库被分成n个分区，并在每个分区中采用过滤阈值来处理候选项集生成；其后产生了一些列基于SWF的改进算法，Li H.F.等人提出一种有效的基于bit的挖掘算法，该算法由三个阶段组成[8]，第一个是窗口初始化，每个事务中的每个项目被编码为有效的比特序列表示；其次，左移技术用于在窗口滑动阶段期间有效地滑动窗口；最后，在模式生成阶段期间水平生成当前滑动窗口中的完整频繁项目集；(3)基于树结构的增量挖掘：以FP-Tree为代表的树结构大大提高了频繁项集挖掘效率。Koh J.L.等提出了AFPIM算法[9]，该算法仍然采用FP-Tree存储数据，但其设置了一个低于最小支持度阈值的参数preMinsup，在树中保留支持度大于preMinsup的项目才会保留在树中，一定程度上避免增量挖掘时对数据库的重复扫描，但当先前“不频繁”的项在更新的数据集中变得“频繁”时，AFPIM算法不能仅通过调整原始树中的项目来生成更新的FP-Tree，它需要重新扫描整个更新的数据集以构建新的FP-Tree；为了避免树的重新构建，CATS-Tree[10]和Can-Tree[11]相继被提出，但是他们的压缩度又不够。

如今，大数据时代的到来，传统串行算法在计算效率、可扩展等方面均不能满足需求。Li N.等人提出基于分布式处理框架的PApriori算法[12]，其是标准Apriori的简单分布式实现，但是仍需要多次扫描数据库；基于FP-Tree和Can-Tree的并行实现算法IncMiningPFP和IncBuildingPFP被提出[13]；上述基于Hadoop MapReduce的并行算法虽在性能上取得不同程度的改进，然而通过磁盘进行大量读写操作极大地限制了它们的性能。Qiu O.H.等人提出了YAFIM算法[14]，该算法充分利用了Spark框架的RDD编程和基于内存的并行计算等特点，大大提高了挖掘效率；Yang S.等人引入一种新的基于矩阵的剪枝方法[15]，减少候选项集的数量，避免不必要的搜索开销；Sethi等人利用垂直布局解决了每次迭代过程中扫描数据集的问题[16]。

综上所述，目前大多数算法，在进行增量挖掘时不能有效利用原始挖掘结果，仍需重新扫描原始数据库，以及重新构建树造成极大的资源浪费；而并行算法虽然使得挖掘性能得到了进一步提升，但基于Apriori的多次数据库数据库扫描和基于树结构的巨大树结构调整代价，成为了目前并行算法的瓶颈。本文结合一种新的树结构，避免了原始数据库的扫描和高昂的树结构调整代价，并通过设计有效的RDD转换策略和负载均衡优化方案实现高效的并行频繁模式挖掘。

2 全压缩频繁模式树及树结构调整策略

2.1 全压缩频繁模式树(FCFP-Tree)

在增量挖掘过程中，为了避免重新扫描原始数据集和重构树结构的开销，本文采用FCFP树结构压缩和存储原始数据集。

定义1FCFP-Tree：FCFP-Tree是一种树结构，FCFP树由四部分组成。第一部分是根节点，标记为“null”.第二部分是所有子项的树，项目前缀子树为根。第三部分是用于存储频繁项目的头表。第四部分是用于存储不频繁项目的头表。

项前缀子树中的每个节点由四个域组成，FCFP树的节点结构定义如下：

Struct FCFPNode {

Int NodeCount；

String NodeItem；

Struct FCFPNode * NodeParent；

Struct FCFPNode * NodeLink；

}

NodeItem：节点的名称，可以标识项目。NodeCount：节点的统计计数，是NodeItem标识的项的相应支持计数。NodeParent：指向FCFP-Tree中父节点的指针。沿指针一直向上搜索，最后指向根节点。NodeLink：指向FCFP-Tree中同一NodeItem的下一个节点的指针。也就是说，所有具有相同名称的项目都与FCFP树中的NodeLink指针相连。

头表中的每个项目由三个字段组成：NodeItem，NodeCount和NodeLink.头表中的项目按其支持计数按降序排列。

定义2节点压缩：如果树包含单个路径P，则P中的所有项目将被压缩并存储在一个节点上，该节点的支持表示为P中任何节点的支持。

FCFP-Tree构造算法类似于FP-Tree算法，除了FCFP树存储完整的项集。为了进一步压缩不频繁项目的存储，通过定义2，在单个分支中具有相同计数的不频繁项目的项目存储在同一节点上。

2.2 有效的FCFP-Tree更新策略

在增量挖掘过程中，项目频率将不断改变，即从最初的不频繁到频繁或从最初的频繁到不频繁。在此过程中，涉及复杂的树结构更新。

更新FCFP-Tree涉及两个步骤：(1)调整与原始数据对应的树结构。FCFPIM首先扫描新添加的数据集并相应地更新头表，然后根据头表中每个项的相对位置变化调整节点路径得到调整后的树结构；(2)再次扫描新增的数据集以将事务添加到调整后的树结构，并修改每个节点对应的计数，得到最终的树结构。其中步骤(2)相对简单，针对步骤(1)，树结构调整包含两种情况：1)频繁项目的调整策略；2)涉及不频繁项目的调整策略。每种情况又涉及相邻节点和和非相邻结点间的调整，具体调整见文献[4].

该两阶段的调整策略避免了每扫描一条事务就调整一次树结构的复杂调整代价，而是根据更新后的头表一次性调整好树结构后，后续直接将新增数据集涉及到的项目计数增添进去，从而大大节省了树结构调整代价。

3 基于Spark的FCFPIM并行算法及RDD转换策略

3.1 FCFPIM并行算法概述

Spark是一种基于内存的迭代式计算框架，其尽量将中间数据放置在内存，并将这些数据集抽象为RDD(弹性分布式数据集)对象，然后采用一系列的算子来处理这些RDD，并将处理好的结果以RDD的形式输出到内存或以数据流的方式持久化写入到其它存储介质中。Spark通过RDD间转换形成的DAG关系，即Lineage(血缘关系)来实现高效的容错。因此，Spark能很好地适应频繁模式挖掘这种反复迭代的数据处理。

基于Spark的FCFPIM算法由两个部分组成，第一部分是对原始数据的挖掘，第二部分是对增量数据进行挖掘。基于Spark模型并行化的FCFPIM算法具体过程描述如下：

Step 1：采用TextFile从HDFS中读取数据集并转化为RDD，将存储事务集的RDD记作TransactionRDD.

Step 2：并行计算原始数据1项集的支持度，然后按照支持度降序对1项集排序，得到原始数据集头表，记为DescendItem1.

Step 3：原始数据采用关联分组策略分组。将TransactionRDD中存储的事务集根据DescendItem1中的顺序进行排序，然后按照关联分组策略对事务集进行分组，得到存储组号以及划分到对应分组的项，记为Group_list.

Step 4：对TransactionRDD中所存储的事务，将每个项所属的事务根据Group_list的分组规则划分到该项所属的组中，然后对每一个组建FCFP树，进行频繁模式挖掘。

Step 5：集群各个节点的任务执行完毕后，将各部分结果聚合，得到原始数据挖掘结果，并将结果输出到HDFS中，即原始数据的挖掘完毕。

Step 6：增量数据进行挖掘开始，读入新增数据，并行计算该数据中的1项集以及支持度，记为NewItem1.

Step 7：将原始数据集头表DescendItem1和NewItem1进行对比判断，得到需要调整的节点以及节点路径，通过广播的形式分发到各任务中。

Step 8：将增量数据按照增量部分的关联分组策略，进行分组并且将数据划分到对应的分组中，进行树结构的调整。

Step 9：对每个更新后的FCFP树进行频繁项集挖掘，待集群各个节点任务执行完毕后，对结果进行聚合，得到增量数据挖掘的结果，并将结果输出到HDFS中。

3.2 有效的RDD转换策略

RDD是Spark的核心，是Spark中最基本的数据抽象。RDD 的操作分为转换(Transformation)和动作(Action)操作。转换就是从一个 RDD 产生一个新的 RDD，而动作就是进行实际的计算。 Spark 里的计算都是通过操作 RDD 完成的， RDD之间会形成类似于流水线一样的前后依赖关系，即形成逻辑上的DAG，任务执行时，可以按照DAG的描述，执行真正的计算，因此，合理有效的DAG策略对算法性能会产生很大程度的影响。

通过对RDD缓存策略的优化，对FCFPIM算法的RDD转换策略进行探索，给出一种有效的RDD转换策略。对应于3.1节描述的步骤，优化的RDD转换策略被分为原始数据挖掘对应的RDD转换(见图1)和增量频繁项集挖掘的RDD转换(见图2).

在图1stage0中，数据被划分为p个分区， 并通过TextFile将数据转化为TransactionRDD， 接着将数据集拆分成各个事务转换成SplitTransactionRDD，并且将其缓存到内存中。Stage1中的itemRDD通过reduceByKey算子的操作转化为item1RDD，获得了1项集且按频率从高到低对项目进行排序，生成项目和索引的映射DescendItem1Map.Stage2中得到关联分组的结果AssociationGroup.stage3根据关联分组的结果将项目划分为p个组，每个组具有唯一的组ID.对数据SplitTransactionRDD中的每一条事务按照关联分组的策略生成每组的事务集，每个事务集中的事务都是完整的，如GenCondTransRDD中。stage4条件模式库通过GroupID缩减为不同的数据分区，每个分区都由具有相同GroupID的库组成。首先为每个组生成一个FCFPTree，并将其存储在FCFPTreeRDD中。然后，挖掘每个FCFPTree生成频繁项FrequentItemRDD.

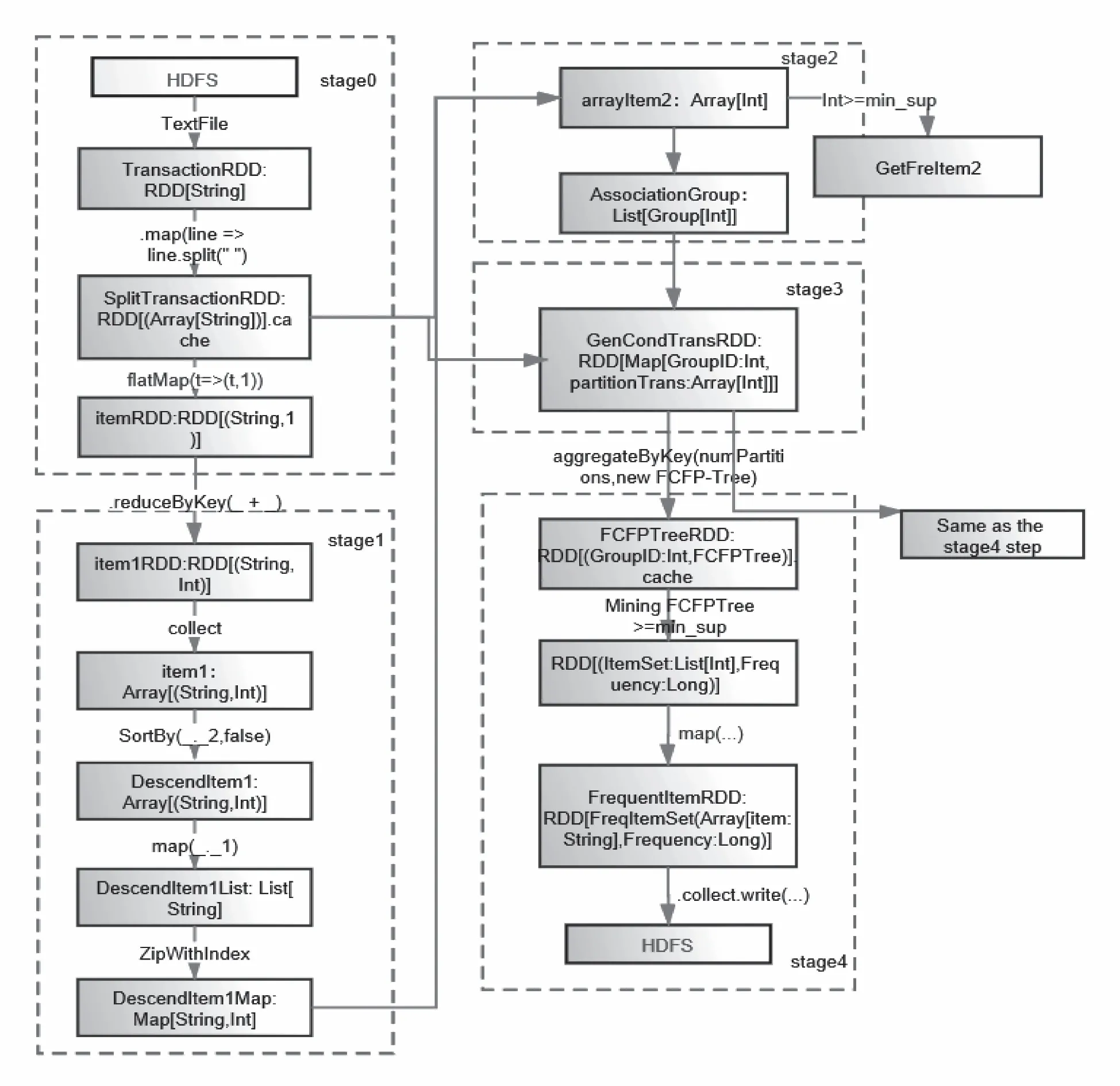
图1 原始频繁项集挖掘RDD转换图Fig.1 RDD conversion diagram of original frequent itemsets mining

图2中stage0到stage4对应原始频繁模式的挖掘。Stage5读入新数据，将事务进行拆分生成SplitIncreTransRDD，缓存到内存中，为方便更新树的时候插入新数据。并且根据后面第4节提出的分组策略将数据划分到对应分组。 Stage6将原始数据集的1项集与新增1项集进行整合，生成新的1项集NewItem1RDD.Stage7将新的1项集进行降序排序，将降序后的新1项集与stage2中的SortItem1Map进行对比，得到需要调整的节点以及其调整的路径，存储在AdjustItem中。接着通过广播变量的形式，将AdjustItem分发到对应的节点上，对FCFP-Tree进行更新。Stage8生成的每个分组对应的事务集存储在GenCondTransRDD中。stage9挖掘每个FCFPTree生成频繁项FrequentItemRDD.

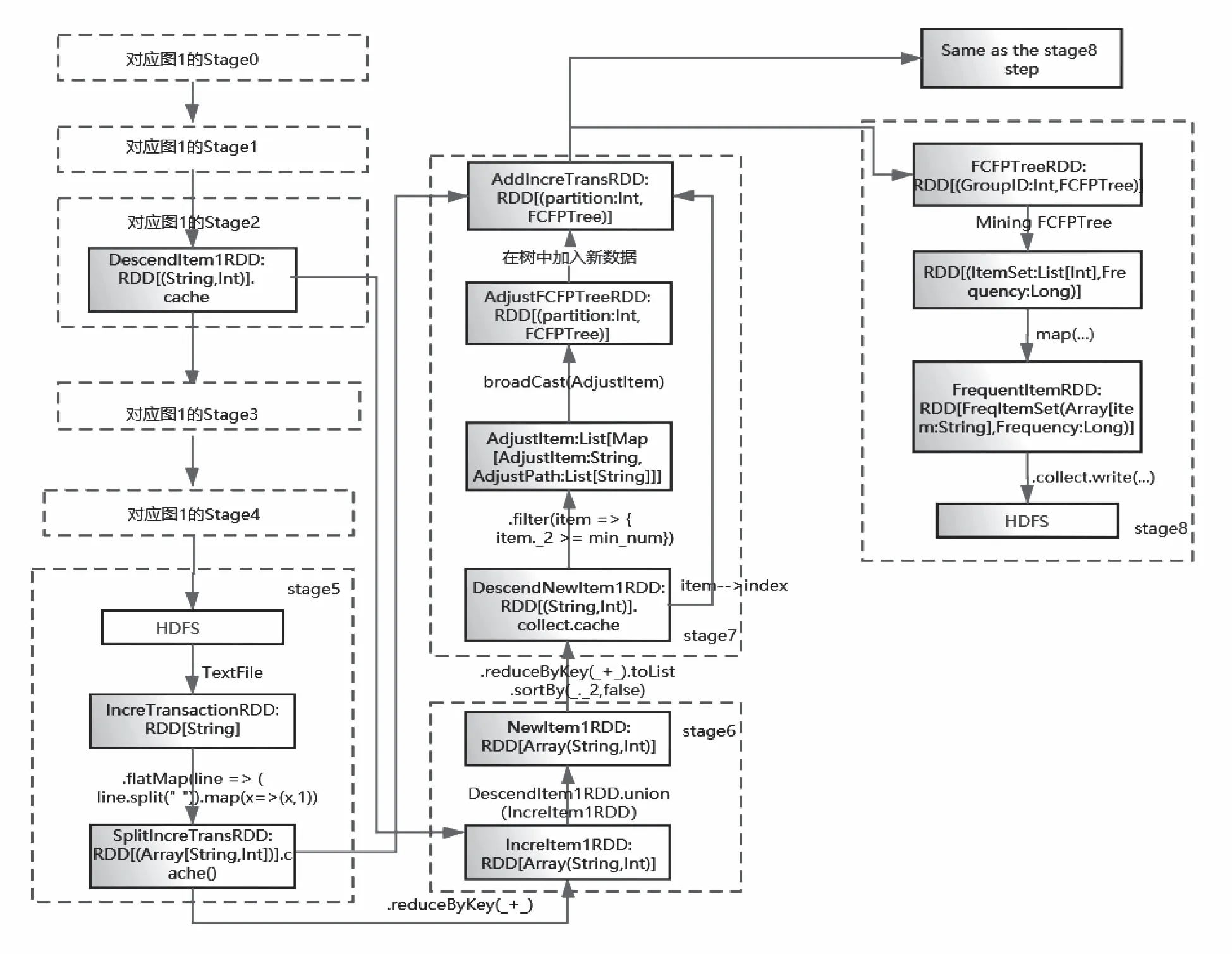
图2 增量频繁项集挖掘的RDD转化图Fig.2 RDD conversion diagram of incremental frequent itemsets mining

由图1和图2可以看出在实现FCFPIM算法过程中，综合选取避免shuffle和复杂度较小的算子进行RDD的转化以及进行了合理的RDD缓存，尽量将多次使用的RDD缓存下来(如：SplitTransactionRDD)，避免RDD的重复计算，在一定程度上提高了RDD缓存命中率。

4 关联分组

在图1中stage2的AssociationGroup操作和图2stage5的SplitIncreTransRDD操作都涉及在并行计算过程中被计算项目的分组问题。在集群系统中，每个节点都可以处理一部分负载，针对关联规则并行算法，项目分组策略一方面会影响集群中各节点的计算负载，另一方面会影响数据的冗余发送和存储。而现有项目分组一般都采用哈希分组，无法保证集群的负载均衡，也没有考虑数据的冗余问题。因此，我们提出了关联分组的策略。

FCFPIM算法挖掘频繁模式仍然采用传统FP-Growth的递归挖掘过程，考虑到递归挖掘过程中，树越高，递归所用的时间越多，而项目支持度越高，对应的事务数越多，树的高度越低；反之亦然。因此，关联分组策略的基本思想是：为保持集群的负载均衡，支持度大的项目尽量与支持度小的项目混合分组，同时为了减少数据的冗余存储，相关性高的项目应该分为一组。由此，频繁项与非频繁项得到了相对均匀的分配。

该关联分组采用了一种压缩二项集存储矩阵ArrayItem2，表1为一个二项集存储矩阵实例。

以表1为例，对关联分组过程描述如下：

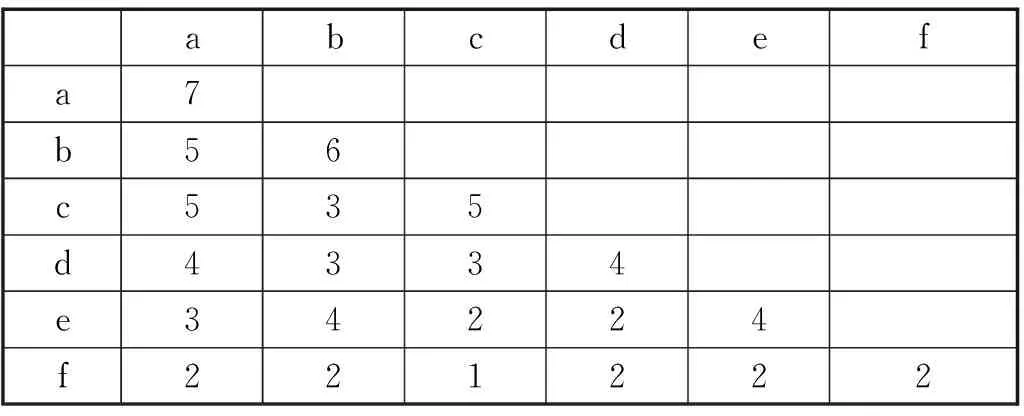
表1 二项集存储矩阵Tab.1 2-itemset count matrix

Step 1：对Item1顺序分组，每组元素的个数为groups个，记为fristStepGroup ={{a，b}，{c，d}，{e，f}}.

Step 2：取fristStepGroup中的元素fristStepGroup(0) = {a，b}与fristStepGroup(1) ={c，d}，进行关联度分组：对fristStepGroup(0)与fristStepGroup(1)做笛卡尔积运算得item2={(a，c)，(a，d)，(b，c)，(b，d)}.

Step 3：在Item2RDD中查找每个item2的支持度计数：(a，c)=5，(a，d)=4，(b，c)=3，(b，d)=3 若最大值只有一个，那么取最大值的组合分为一组：(a，c).若最大值有多个，则选取第一个出现的最大值的组合。

Step 4：去掉item2中带a和c的组合，重复Step4步，直到item2的长度为0.得到的结果为groups：(a，c)，(b，d).

Step 5：删除fristStepGroup(0)，若fristStep-Group的长度不为0，则执行第三步得item2={(c，e)，(c，f)，(d，e)，(d，f)}.执行Step3 (c，e)=2，(c，f)=1，(d，e)=2，(d，f)=2，得到(c，e)将e加入到(a，c，e).执行Step4得到(d，f)将f加入到(b，d，f).

最终，groups={group0={a，c，e}， group1= {b，d，f}}， group0对应数据分区对项a，c，e是完备的，group1对应数据分区对项b，d，f是完备的。对每个分区中的事务分别建立FCFP树，并且进行频繁项集挖掘。增量数据的新增项目分组一是基于调整后的二项集存储矩阵，在此不再赘述，具体分组算法见算法1：

算法1：关联分组

输入：Item1，ArrayItem2

输出：groups

0： val item1 = item1RDD.toList

1： val group_num = (item1.count+1 + group_size-1) / group_size

2： //将item1按顺序分为group_num个组，每个组小于或等于group_size个元素

3： val fristStepGroup = new ListBuffer[ListBuffer[String]]

4： for(i <-1 to group_num){

5： val k = (i-1)*group_size +1

6： val group_list = new ListBuffer[String]()

7： for (j <- k to Item1.length){

8： if( j % group_num !=0){

9： group_list += Item1(j-1)

10： }else{

11： group_list += Item1(j-1)

12： break

13： End If

14： End For

15： fristStepGroup += group_list

16： End For

17： for (i <- fristStepGroup.length-1){

18： If (i+1 <=fristStepGroup.length-1 ){

19:val item2 = fristStepGroup(i) Cartesian(fristStepGroup(i+1))

20： 在ArrayItem2中查找每个item2的支持度计数

21：得到item2中的最大值(Max._1，Max._2)

22： Gruops+= (Max._1，Max._2)

23：删除item2中带Max._1和Max._2的组合

24： End If

25： End for

5 实验结果及分析

本次实验搭建了Spark On YARN的完全分布式集群，在VMware Workstation 上创建三台虚拟机作为集群的节点，具体配置见表2.

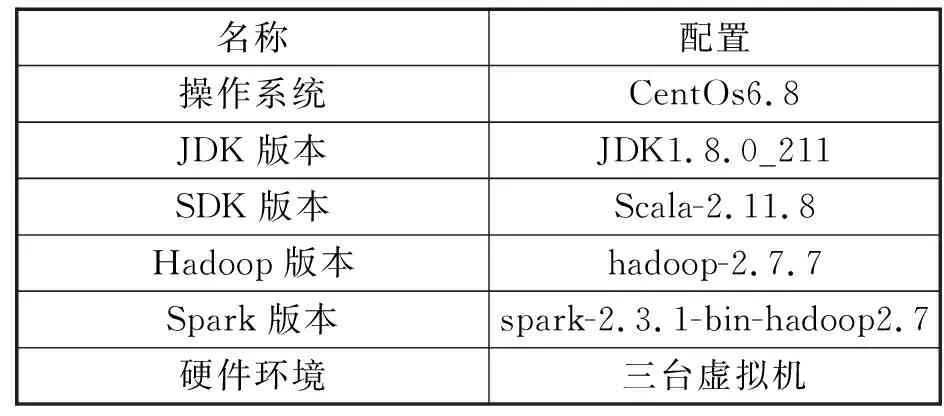
表2 集群系统环境配置Tab.2 Cluster environment configuration

为了评估FCFPIM算法的性能，与经典的基于Spark的并行FPGrowth算法与最新的基于Spark的并行EFUFP算法进行了对比。数据集采用IBM Quest Market-Basket生成器产生，其可以灵活配置以创建各种数据集，来满足各种测试需要的需求。

5.1 不同规模数据集对算法性能的影响

该组实验采用T10I4D系列和T40I10D系列各4组不同事务数的数据集(事务数分别为10万，20万，30万和40万条)，对三种算法的运行效率进行评价，其中，增量数据的大小大约是原始数据大小的10%，最小支持度设为0.9%.具体实验结果见图3和图4.

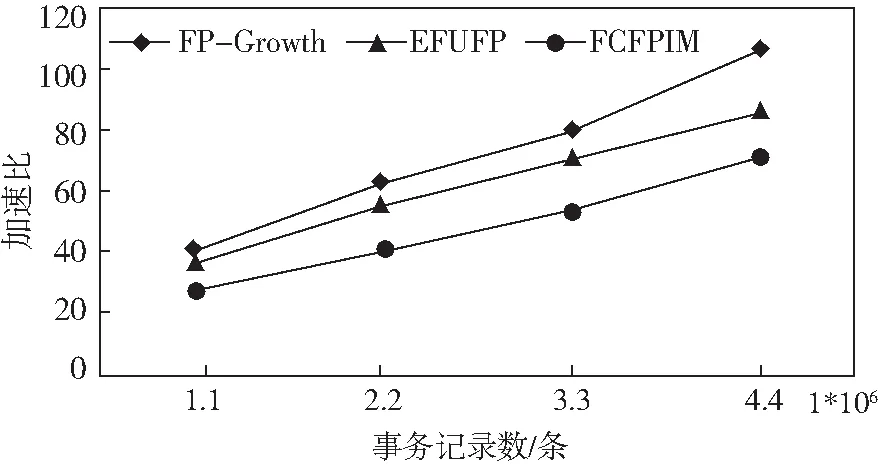
图3 在数据集T10I4D上的执行时间对比Fig.3 Execution time on the data set T10I4D

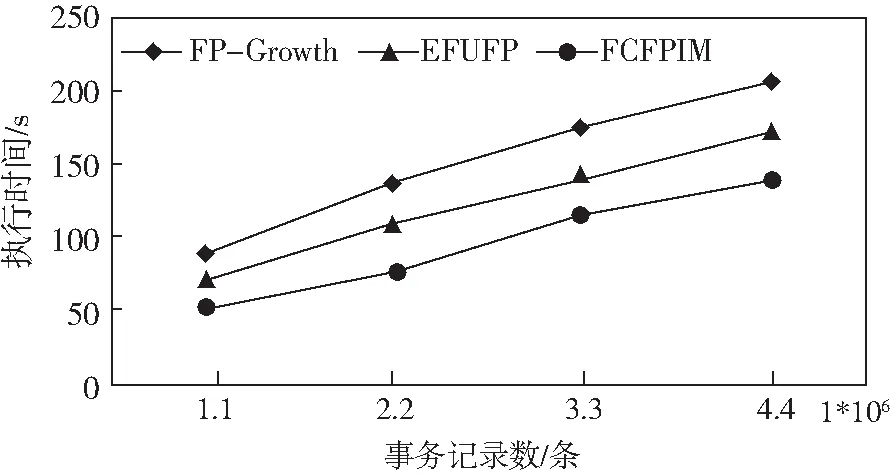
图4 在数据集T40I10D上的执行时间对比Fig.4 Execution time on the data set T40I10D

从图3和图4可以看出，FCFPIM算法性能表现最优，并行FP-Growth最差，这主要是因为FP-Growth在增量过程中，采用最直接的方式，重新建树挖掘，因此消耗的时间比较长，而EFUFP算法则在增量挖掘阶段采用了高效的调整策略。本文的FCFPIM算法一方面通过考虑项目之间的关联程度，对项目进行均衡分组，使得分组后各数据分区对应的冗余存储大大减少，对应每个分区的计算量亦会下降，且均衡的分组进一步提高了资源利用率，同时，有效的缓存策略使得一些被多次使用的RDD不再需要重复计算，从而进一步加速了FCFPIM算法的执行。

5.2 不同支持度对算法性能的影响

本组实验采用事务数为10万条的T40I10D的数据集，并将支持阈值分别设置为0.5%，0.7%，0.9%，1.1%，1.3%进行测试。

从对比结果图5可以看出,随着支持阈值的增加,生成的频繁项集数目会减少,挖掘的时间会减少,这符合理论上的运行趋势。

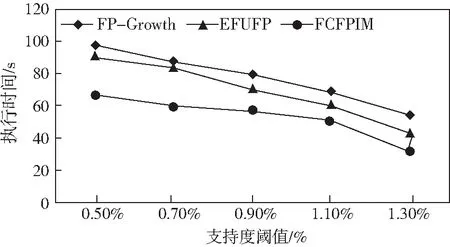
图5 不同支持度的执行时间Fig.5 Execution time with different support

5.3 可扩展性

集群的节点数量对算法的执行时间有着最重要的影响，本组实验采用与上组实验同样的数据集，支持度计数设置为0.9%进行测试，测试结果如图6所示。

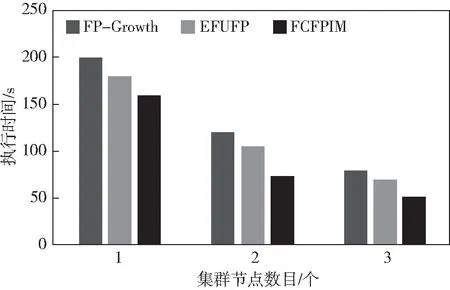
图6 可扩展性Fig.6 Scalability

通过图6可以明显看出，随着节点数的增加，三个算法整体挖掘时间均减少，因为，可用的计资源随之增加。在只有一个计算节点的时候，FCFPIM算法与EFUFP算法的执行时间差不是很明显，因为只有一个节点，分组策略是无效的，所以两个算法的执行时间差距不大，完全取决于算法本身的性能与FCFPIM算法的缓存策略。随着计算节点数目的增加，基于关联分组策略优势逐渐体现出来。

5.4 加速比

加速比为并行算法在一个计算节点上的执行时间与在多个计算机节点上的执行时间的比值。从图7中可以看出，随着集群计算节点数量的增加，三个算法的加速比大致呈现出线性关系，说明三个并行的算法都是有效的。整体上随着集群计算节点数目的增加，三个算法的执行时间差越来越大。因为FCFPIM拥有合理的分组策略。随着计算节点的增加，关联分组的策略会有明显的优势，因此FCFPIM并行算法的性能要更好一些。

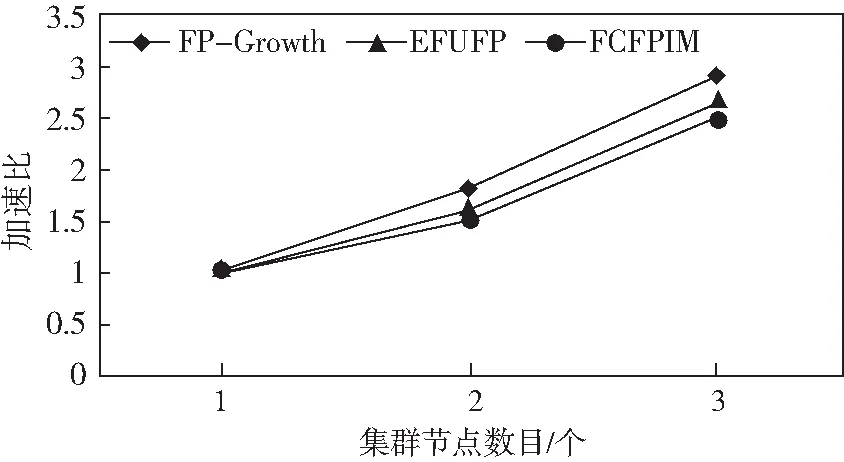
图7 加速比Fig.7 Speedup

6 总结与展望

针对传统增量挖掘存在重复扫描原始数据集或树结构调整成本过高等问题，以及面对海量数据处理传统串行计算不足以应对的问题，提出一种基于Spark并行框架的并行增量频繁模式挖掘算法FCFPIM，FCFPIM综合考虑了负载均衡，RDD的shuffle成本，缓存策略等问题。而由于FCFP树包含完整的项目信息，因此该空间开销会对算法的可伸缩性产生不利影响。作为未来的研究方向，我们将引入一个度量来确定如何合理的将项目保存在树结构中。该度量的定义将考虑数据的特征以及新数据与原始数据的比率。此外，FIM的实际应用也值得关注。