基于单标签图像标注的损失函数分析
2020-11-04邓建国张素兰
邓建国,张素兰
(太原科技大学计算机科学与技术学院,太原 030024)
有监督学习利用有标记的样本调整模型参数,使模型具有正确预测未知数据的能力,其目的是通过让计算机学习一组有标记的训练数据集,进而获得新的知识或技能,这就要求计算机不断学习样本数据,并依据样本真实值与预测值之间的损失调整模型参数,提升模型的判别能力。因此,损失函数的合适选取影响着有监督学习的广泛应用。
图像标注是有监督学习中的一个典型应用,已广泛应用于图像检索、图像分割和目标检测等领域。图像标注根据图像获得的标签数量,大致分为单标签图像标注和多标签图像标注。基于有监督学习的单标签图像标注方法是根据标注规则,利用损失函数值调整模型参数为图像分配唯一的预定义标签。与多标签图像标注相比,单标签图像标注模型分配的标签数量更少,算法更简单,模型对损失函数的影响更小,更适合研究损失函数的特性以及不同损失函数在度量数据样本上的差异。单标签图像标注或分类中常使用MNIST数据集验证算法的有效性,Gu等人[1]使用MNIST验证了同时学习一个合成字典和一个解析字典的方法,高子翔等[2]使用MNIST验证了基于自适应池化的双路卷积神经网络。本文基于神经网络模型,在MNIST数据集上构建单标签图像标注方法对比研究有监督学习的常用损失函数。
有监督学习算法使用的损失函数比较多,典型的损失函数包括平方损失[3]、绝对损失[4]、0-1损失[5]、hinge[6]、余弦损失、对数损失[7]和交叉熵损失[8]以及它们的演化形式等。本文依次选用均方误差(Mean Squared Error,MSE)、平均绝对误差(Mean Absolute Error,MAE)、均方对数误差(Mean Squared Logarithmic Error,MSLE)、铰链损失(hinge)、二分类交叉熵损失、多分类交叉熵损失、余弦损失中的一个作为神经网络模型的损失函数构建7个图像标注子实验,每个子实验除损失函数不同外,其他的实验环境完全相同。通过实验结果分析,探索损失函数与数据集的内在联系,在实验的基础上,提出新的组合损失函数,并利用单标签图像标注方法验证了提出的组合损失函数的有效性。
1 神经网络模型
神经网络模型是由大量的神经元互相联接形成的复杂网络系统,具有大规模并行、分布式存储、自组织、自适应和自学习能力。本文以神经网络模型为基本模型,使用图像研究领域的通用数据集MNIST研究损失函数的特性。目前在机器学习领域流行的神经网络算法框架主要有caffe、keras和tensorflow等。其中keras具有易用理解、操作简单等优点已广泛应用于图像处理领域。
2 基于单标签图像标注的损失函数分析
基于神经网络构建的单标签图像标注方法是利用图像底层特征相似性,采用损失函数度量模型的预测值与样本真实值之间的误差,进而为未知图像标注一个预定义标签。算法的构建过程包括图像预处理、模型构建和模型训练与评估。在构建的单标签图像标注算法中,损失函数作为算法的一个输入参数,通过更换损失函数,对比研究常用损失函数的性能差异。
2.1 图像预处理
在使用神经网络模型的算法中,对图像进行预处理不仅能加快神经网络的收敛速度、防止梯度爆炸,而且能提高神经网络模型的预测准确度。本文算法使用keras的数据读取工具将MNIST数据集划分为训练数据集、训练标签集、测试数据集和测试标签集,其中训练数据集、测试数据集中的图像向量需降维和归一化,训练标签集和测试标签集中的标签向量需转换为独热编码。图像向量降维和标签向量转独热编码采用python函数实现,降维后的图像向量除以255实现归一化。
2.2 模型构建
算法使用keras的序列化模型构建神经网络模型,模型结构如图1所示。模型构成为:输入层由dense_1和dropout_1组成,该层有784维输入,512维输出,共有401 920个参数;隐层由dense_2和dropout_2组成,该层有512维输入,512维输出,共有262 656个参数;输出层为dense_3,该层有512维输入,10维输出,共有5 130个参数。

图1 本文构建的模型结构Fig.1 Model structure
模型的损失函数、优化器以及模型的性能评价指标采用keras库函数实现。模型的优化器使用RMSProp、性能评价指标使用准确率和损失值。在每个子实验结束后,将实验结果写入对应的文件中。模型的参数设置见表1.

表1 模型参数设置Tab.1 Model parameter setting
2.3 训练与评估
实验由7 个子实验构成,每个子实验都是一个独立的图像标注算法。每个子实验都进行50次迭代训练,在每次迭代过程中,算法批量选取样本,每批次样本个数为128,每批次训练结束后计算一次训练准确率和训练损失值,共需195个批次;在每次迭代结束后,计算并保存本次迭代的训练准确率、训练损失值、验证准确率和验证损失值。在全部迭代结束后,算法生成每个子实验的准确率和损失值曲线图。在每个子实验训练结束后,使用测试集评估模型的预测性能,汇总每个子实验评估模型算法输出的准确率和损失值,进一步研究损失函数度量样本的性能差异。
3 构建组合损失函数
目前有监督学习应用推广中损失函数的使用大致分为三种情况,一是使用模型默认的损失函数,二是在实验的基础上选择与求解问题相匹配的现有损失函数,三是构建新的损失函数。第一种情况的不足是算法选用的损失函数往往是针对原有问题的,如果仍使用默认损失函数度量新问题,可能会因损失函数不适合度量新问题而降低模型的性能;第二种情况的不足是尽管现有损失函数非常多,但相对于应用推广中的待求解问题而言就少的多,也就是说,现有损失函数还不能完全准确地度量待求解问题的数据样本。与前两种情况相比,发挥每个损失函数度量数据的优势共同度量待求解问题,不仅实验过程简单,而且往往能取得很好的预测效果。通常情况下,构建损失函数的方法是选择与求解问题相匹配的一个或多个损失函数,改进现有损失函数演化为新的损失函数或组合现有损失函数构成新的损失函数。与演化损失函数相比,组合损失函数更容易实现,更适合有监督学习算法的快速推广。
组合损失函数的组成原则一般是根据求解问题的性质,利用损失函数的优点,将现有的损失函数采用四则运算方式组合,然后在实验的基础上调整权重,提高模型的预测准确率。本文从单标签图像标注实验中选择预测率高的二分类交叉熵、多分类交叉熵、MSLE和MSE构建组合损失函数,并利用单标签图像标注实验验证组合损失函数的可行性,构造的损失函数权重α和β的值都设置为1,见表2.

表2 组合的损失函数Tab.2 Combined loss function
4 实验结果与分析
4.1 数据集与参数设置
MNIST是图像处理领域的一个通用数据集,它由训练集和测试集两部分组成,其中训练数据集包含60 000个样本,测试数据集包括10 000个样本。交叉验证(cross-validation)是一种评价模型分析结果是否可推广到一个独立的数据集上的方法。本文的单标签图像标注方法采用留出法(holdout cross validation)将MNIST数据集中的60 000个训练样本划分为训练集和验证集,其中训练集包括55 000个样本,验证集包括5 000个样本。
基于神经网络的算法一般通过优化由损失函数构成的代价函数进行训练,在不影响训练效果的前提下,通常要求模型必须在最短的时间内收敛,即通过优化算法更新参数值,使代价函数最小化。本文模型的优化算法采用RMSProp,其参数设置见表3.

表3 RMSProp算法参数设置Tab.3 Rmsprop algorithm parameter setting
4.2 性能评估指标
性能评估指标常用于评估模型性能的优劣,一般情况下,模型性能的评估主要包括训练过程中对模型性能的评估和预测过程中对模型性能的评估。实验使用有监督学习领域广泛使用的精确率(Precision,P)、召回率(Recall,R)、准确率(Accuracy,acc)和损失函数值(loss)作为评价指标。
4.3 基于单标签图像标注的损失函数对比分析
每个子实验中,神经网络模型依次选用MSE、MAE、MSLE、hinge、二分类交叉熵损失、多分类交叉熵损失和余弦损失中的一个作为损失函数进行训练,每个子实验都生成一个准确率和损失值曲线图,最后汇总多个子实验的预测结果形成模型预测的准确率和损失值汇总图。
4.3.1 准确率和损失值
1)MSE的准确率和损失值如图2所示,经过50次迭代后,训练准确率、验证准确率、训练损失值和验证损失值分别为:99.02%、98.23%、0.001 6和0.003 0.

图2 MSE的准确率损失值曲线图Fig.2 MSE accuracy loss curve
2)MAE的准确率和损失值如图3所示,经过50次迭代后,训练准确率、验证准确率、训练损失值和验证损失值分别为:98.30%、97.86%、0.003 5和0.004 3.
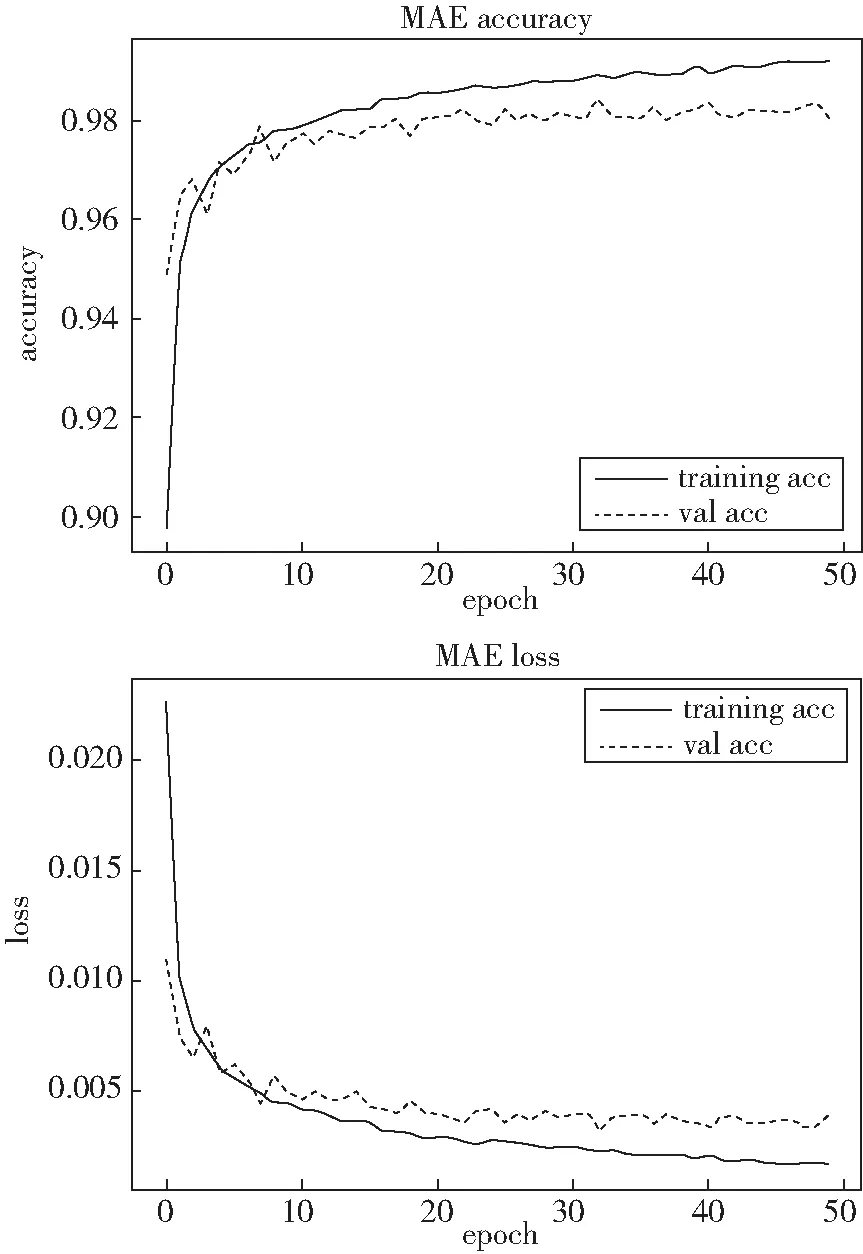
图3 MAE的准确率损失值曲线图Fig.3 Mae accuracy loss curve
3)MSLE的准确率和损失值如图4所示,经过50次迭代后,训练准确率、验证准确率、训练损失值和验证损失值分别为:99.06%、98.23%、0.000 7和0.001 4.

图4 MSLE的准确率损失值曲线图Fig.4 MSLE accuracy loss curve
4)hinge的准确率和损失值如图5所示,经过50次迭代后,训练准确率、验证准确率、训练损失值和验证损失值分别为:98.21%、97.78%、0.90和0.90.
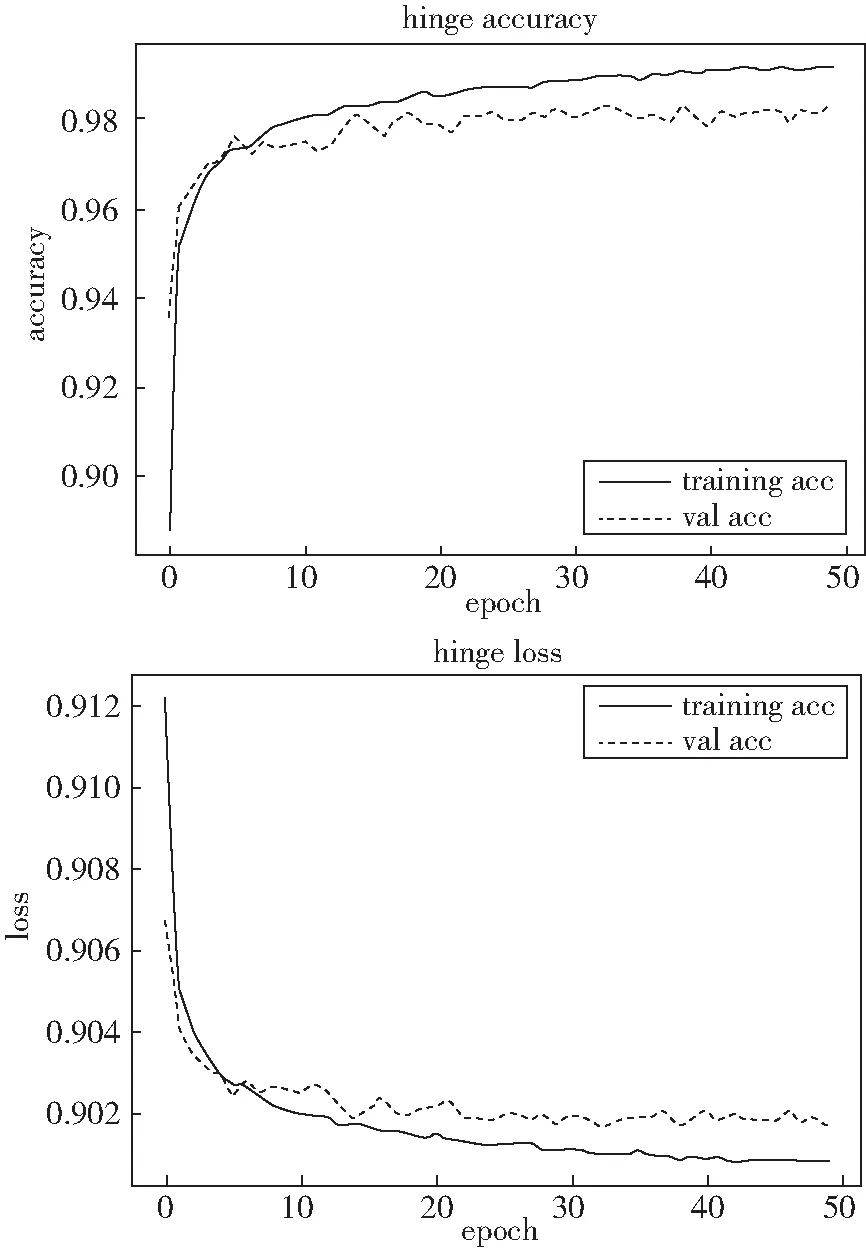
图5 hinge的准确率损失值曲线图Fig.5 Hinge accuracy loss curve
5)余弦损失的准确率和损失值如图6所示,经过50次迭代后,训练准确率、验证准确率、训练损失值和验证损失值分别为:98.84%、98.13%、-0.989 6和-0.982 8.

图6 余弦损失的准确率损失值曲线图Fig.6 Accuracy loss curve of cosine loss
6)二分类交叉熵损失的准确率和损失值如图7所示,经过50次迭代后,训练准确率、验证准确率、训练损失值和验证损失值分别为:99.86%、99.66%、0.004 8和0.02.
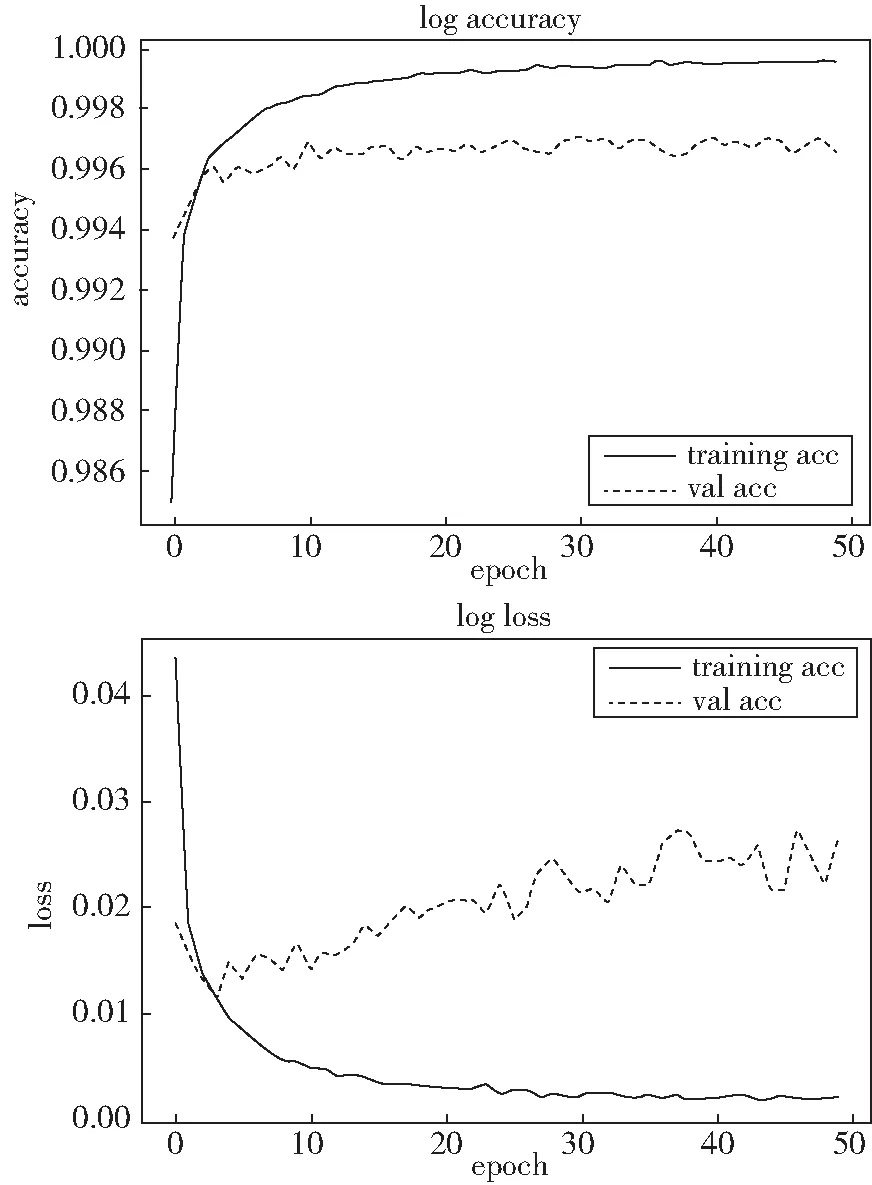
图7 二分类交叉熵损失的准确率损失值曲线图Fig.7 Accuracy loss curve of cross entropy loss in binary classification
7)多分类交叉熵损失的准确率和损失值如图8所示,经过50次迭代后,训练准确率、验证准确率、训练损失值和验证损失值分别为:99.25%、98.22%、0.0276和0.119 0.
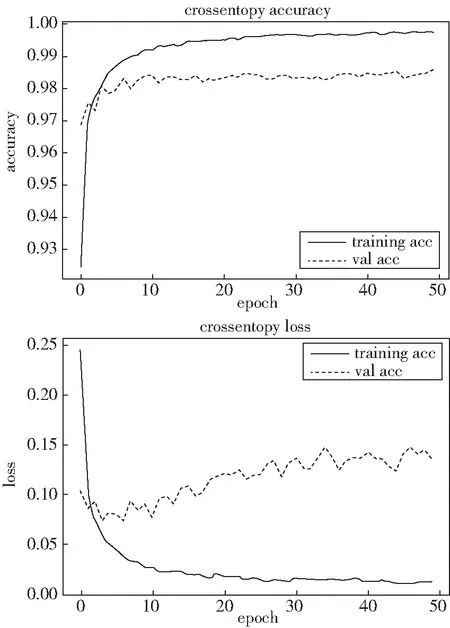
图8 多分类交叉熵损失的准确率损失值曲线图Fig.8 Accuracy loss curve of cross entropy loss of multi-classification
每个对比子实验经50次迭代训练后生成的准确率和损失值如图2-图8所示。从整体上分析实验获得的曲线图可知,模型的准确率和损失值随迭代次数的增加分别呈上升和下降趋势,最终都处于稳定状态。但是,在相同的迭代次数处,每个子实验的准确率、损失值却不同,甚至差异比较大。在实验结果中,出现准确率损失值曲线整体趋势相同的原因是在训练、验证过程中,模型的损失函数都能正确度量样本的真实值与预测值的差异,并且模型依据损失值不断调整模型参数,使模型逐渐稳定。在每个子实验中,除模型的损失函数不同外,其它实验环境完全相同,但每个实验的结果却不同,可知在相同实验环境下,不同损失函数由于其本身特性不同,导致其度量同一数据集中的同一样本的性能存在差异,这就直接导致每个子实验的准确率和损失值不同。
4.3.2 准确率和损失值汇总表
经过50次迭代后,汇总7个子实验的训练准确率、验证准确率、训练损失值和验证损失值形成汇总表,见表4。在表4中余弦损失的数据与其它数据差异较大,余弦损失的损失值出现负数的原因是余弦损失在度量样本时更注重两个向量在方向上的差异,而对具体距离数值不敏感,可见余弦损失不适合度量图像的像素特征。从表4可知,对于灰度图像数据集更为合适的损失函数为二分类交叉熵和多分类交叉熵。

表4 准确率和损失值汇总表Tab.4 Summary of average accuracy and loss
4.3.3 模型预测的准确率和损失值汇总图
为检验各个子实验训练的模型在灰度图像上的预测性能,在每个子实验训练结束后,将测试数据输入到模型评估算法上,评估算法计算后输出模型预测的准确率和损失值,汇总结果如图9,其中cosine的值同样出现异常,为了能直观观察数据,图中cosine的值已做了相应的处理。从图9可知,适合神经网络解决图像标注问题的损失函数为二分类交叉熵和多分类交叉熵,这与前面的实验结果相匹配。

图9 预测准确率损失值汇总图Fig.9 Summary chart of predicted accuracy loss value
4.4 不同模型实验结果对比
针对MNIST数据集,本文选用预测准确率最高的二分类交叉熵损失函数构建的图像标注方法,与DPL(Dictionary Pair Learning)、DDCCNN(dual-channel convolutional neural net)和CNN[9]算法的准确率进行对比,验证本文构建的模型的有效性,对比结果见表5.通过表5可以看出,与传统方法相比,本文构建的算法在MNIST上的预测精确率最高,性能有较大的提升。

表5 不同模型实验结果对比Tab.5 Comparison of experimental results of different models
4.5 组合损失函数的有效性分析
4.5.1 筛选最优组合损失函数
组合损失函数的有效性验证实验由6个子实验构成,每个子实验除损失函数不同外,其它的实验环境完全相同,实验中权重α、β的值均为1.经过50次迭代训练后,每个子实验的最终预测汇总结果见表6.从实验结果可知,组合损失函数都能对图像样本进行度量,并且预测效果很好,可见组合损失函数能有效提升模型的预测准确率,可作为有监督学习推广过程中解决特定实际问题的有效手段。
4.5.2 最优组合损失函数的权重调优
本实验为二分类交叉熵+MSE损失函数进一步选择最优权重参数。实验中α和β的权重依次选择(0.05,0.95)、(0.2,0.8)、(0.4,0.6)、(0.6,0.4)、(0.8,0.2)和(0.95,0.05)进行6次实验,最终的预测结果见表7,从实验结果可知,二分类交叉熵+ MSE的最优权重α=0.95和β=0.05.
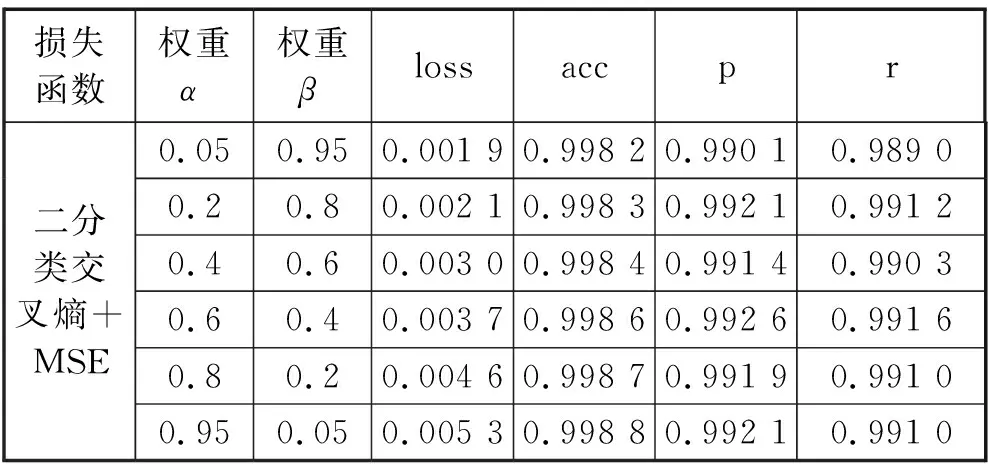
表7 组合损失函数的权重调优结果Tab.7 results of weight optimization of combined loss function
5 结束语
本文主要工作包括两个方面: 1)基于神经网络构建单标签图像标注方法,在MNIST数据集上验证了算法的有效性。2)通过更换单标签图像标注算法中的损失函数,研究常用损失函数的特性,以及损失函数度量图像的性能差异,在实验的基础上,提出了新的组合损失函数,并通过实验验证了组合损失函数的可行性。下一步,论文的工作将重点研究组合损失函数的组合方法和权重调优方法。
