基于核密度估计的离群数据挖掘
2020-11-04赵旭俊苏建花席婷婷
马 洋,赵旭俊,苏建花,席婷婷
(太原科技大学 计算机科学与技术学院,太原 030024)
离群是数据集中存在的、少量的、与大多数对象模式不一致的对象(观察、事例或点)。识别数据中的离群非常重要,因为它们会扭曲常规的分析和决策,也可能是突发事情、异常活动等。异常检测在实际情况下尤其有用,一方面数据集众多,另一方面,它包含或承载了最重要信息的意外事件。但是,在异常检测的通用技术方面存在着一些挑战:离群数据挖掘的应用领域(例如,网络入侵检测、监测、欺诈、机器故障等)不断增加,这为相应的离群数据挖掘方法提出了新要求,同时也增加了难度。另外,现实世界中可用于构建模型的数据通常是未标记的,因此,通过特定的分布或几何形状来确定该区域的先验形状,通常是一项困难的任务,这可能会产生偏差,导致生成的模型失去意义。
为了较好适应不同的数据集和应用领域,在分析密度估计和异常检测的基础上,本文给出了样本点及其邻域的核函数,并提出了一种基于核密度估计的离群数据挖掘算法OMDE.通过对象之间的距离得到每个样本点的邻域;然后计算数据集中每个样本点的密度值,并对其邻域密度进行估计;通过对各样本点的离群因子比较,最终获得偏离大多数对象的离群数据。最后,采用UCI数据集对本文提出的OMDE算法同已有的传统算法进行比较,实验结果显示OMDE算法在效率和准确性两个方面上,体现出较强的优势。
1 相关研究
离群数据挖掘在各种领域中有着广泛的应用。例如,它被广泛用于网络入侵和恶意事件的检测;也被用于识别医疗事故或信用欺诈。研究者们提出了形形色色的离群检测算法,大体可分为以下几类:
1.1 基于聚类的方法
基于聚类的离群数据检测,主要依赖于聚类、分类数据集,然后将稀疏区域的观测值识别为离群数据。该类方法可分为两种:其一是基于排名的离群点分析和检测ROAD[1];其二是基于Rough-ROAD[2]的方法。ROAD方法定义了两种类型的离群值:基于频率的离群值和基于聚类的离群值。基于频率的离群值是那些具有不频繁类别(小平均边际频率)的观测值。相反地,基于聚类的异常值是那些具有频繁类别的罕见组合的观测值。基于Rough-ROAD的方法扩展了ROAD方法,它是在粗糙集理论的基础上,将k-modes算法改进为粗糙k-modes算法,以捕捉不确定性,并处理关于某些聚类的异常值隶属度的模糊性。
1.2 基于密度的方法
基于密度的离群,又称为局部离群[3],旨在识别局部区域中具有离群行为的观测,多数观测通常具有相似的特征[4]。这类离群不同于全局离群,全局离群与大多数其他观测结果的模式不一致,而不仅仅表现在局部区域内[5]。分类数据的局部离群挖掘方法包括超边缘异常检验(HOT)[6],k-局部异常因子k-LOF,监视方法[7]。HOT方法基于定义两组变量:公共变量C和外围变量A,它发展了一个超图来捕捉类别观测之间的相似性。k-LOF是分类和定量数据的局部异常检测方法,将局部异常因子(LOF)扩展到范畴域。如果k-LOF与邻居的关系弱于邻居与邻居之间的关系,则k-LOF将观测值视为局部异常值。WATCH方法包括两个阶段:特征分组和异常点检测。在特征分组阶段,通过将相关变量聚集到同一组中,将q个分类变量集合划分成不相交的特征组。
1.3 基于贝叶斯/条件频率的方法
这类方法对分类中的离群数据定义比较模糊,它搜索具有高边际频率和小联合频率的观测值。换言之,该类方法将异常视为类别组合不频繁的观测,而其类别是频繁的。条件异常与其它异常检测方法所识别的异常有很大区别,该类方法包括条件算法CA,异常模式检测APD,属性关联算法。条件算法CA将异常值定义为具有频繁类别的罕见组合的观测值;异常模式检测方法APD是将异常值百分比高于预期的相关观测组视为离群数据[8];属性关联算法是将条件异常定义为包含频繁类别的观测,但这些项目集很少一起观测。该方法首先从数据中提取一组高度可信的关联规则,然后计算一个叫做离群度的离群分数。
1.4 其他方法
除了上述的几类方法之外,研究者还提出基于指标变量的方法、基于频率的方法以及信息论方法[9]。
基于指标变量的方法[10]是用数值表示分类数据,然后对定量数据进行异常检测。采用这种方法的例子有指标变量法和基于多重对应分析方法。基于频率的方法使用频率(即类别的出现次数)而不是距离来识别离群。有三种频率可用于识别分类数据中的异常:边际频率、项目集频率、以及分散频率。信息论方法[11]背后的思想依赖于异常存在与数据中噪声量之间的直接关系。因此,异常检测问题[12]可以转化为一个优化问题,其目标是找出使内部观测的信息增益最大或不确定性最小化的异常集合。这些方法大多使用熵作为信息增益或不确定性度量,可分为香农熵和全息熵。
2 核密度估计
基于密度估计的离群检测方法通过比较每个样本的密度与其邻域密度来检测异常,邻域密度通常是其邻域的局部密度的平均值。该类方法中,如何合理有效地估计密度,成为一个需重要关注的问题[13]。为解决这一问题,提出了一种新的局部密度估计核函数和加权邻域密度来计算每个样本的异常因子,并用于异常检测。基于加权邻域密度的异常检测方法对邻域大小参数具有较强的鲁棒性。
2.1 邻域的定义
假设D是一个数据集,|D|是数据集D中的数据对象个数,其中x=[x1,x2…xd]是一个d维的数据对象,对于任一正整数k(k≤|D|),x的k距离disk(x)=dis(x,o),是节点x到数据集中节点o的距离,并且满足如下的两个条件:
1)在数据集D中存在至少k个样本点q,使得dis(x,q)≤dis(x,o);
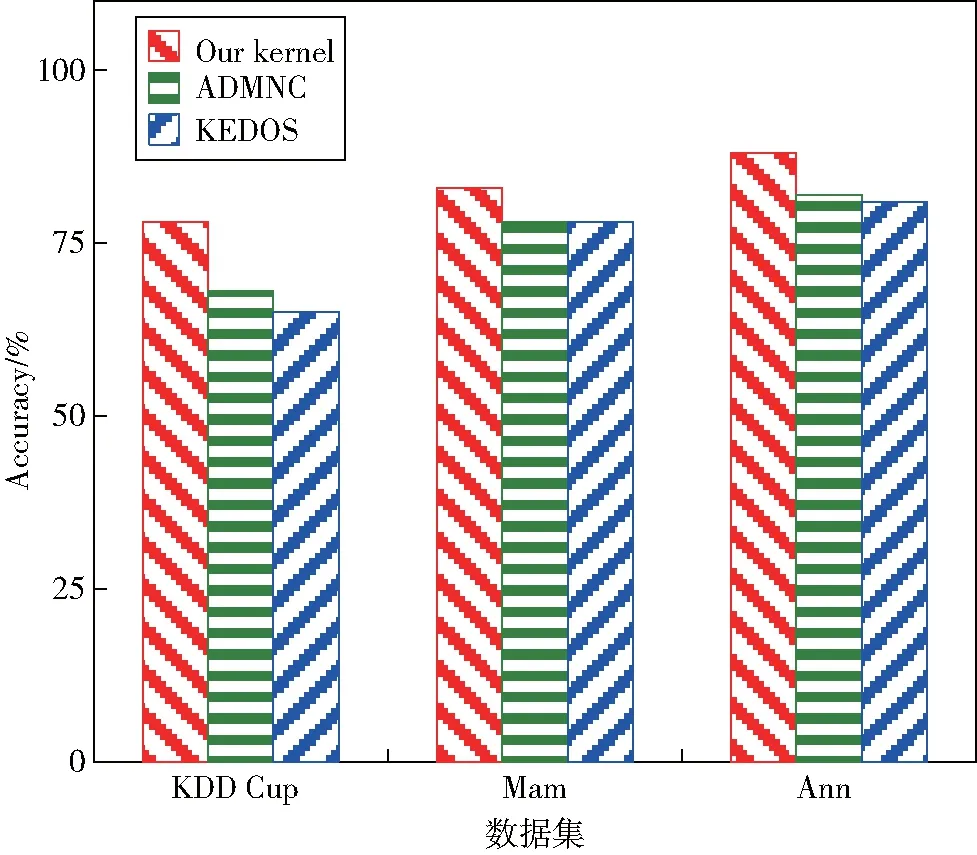
2)在数据集D中最多存在k-1个样本点Q,使得dis(x,q) 基于上述的假设,x的k-距离邻域是由一些特殊的样本点构成,这些样本点到节点x的距离不大于x的k距离,采用Domaink(x)来表示,可形式化描述为: Domaink(x)={q∈D|dis(x,q)≤disk(x)} (1) k-距离邻域中的任一样本节点都是x的k-距离邻居。图1表示了k为3的前提下,节点p1和p2的3-距离邻域,p1的3-距离邻域为以p1为圆心,以p1的3-距离dis3(p1)为半径的圆。同样地,p2的3-距离邻域为以p2为圆心,以p2的3-距离dis3(p2)为半径的圆。显然地,p2的3-距离邻域要小于p1的邻域,即p2的3距离小于p1的3距离。换言之,在单位区域内p2的样本点数量(即p2的局部密度)要大于p1的数量,所以,空间样本中k距离邻域的大小与样本的局部密度成反比。即在以p1为圆心,以p2的3-距离dis3(p2)为半径画的圆中,点的个数一定小于3。因此,在k值不变得情况下,样本点的局部密度越小,这些样本点的k距离越大,该样本点成为离群的可能性将越大。 图1 3-距离邻域Fig.1 3-distance neighbor 样本点的密度大小同离群点特征密切相关,为有效监测离群,需对各样本点的密度进行计算。核密度估计是研究未知总体中随机变量分布特性的重要工具,可用作样本点邻域度量的手段。尤其在可视化数据中,核密度估计比常用的概率密度图(Probability Density Plot,PDP)方法具有更稳定、强壮的性能。核密度估计通过对一组高斯分布求和来估计数据频率,它与概率密度图PDP相反,不需要考虑分析不确定性的影响。这一特点能较好地适用于计算样本点的密度,下面给出核密度计算公式。 设x表示密度为f(x)的随机变量,在本文中,x可看做数据集D中一个具有d维特征的数据对象,f(x)可以近似表示为: f(x|h)=f(x)*Kh(x) (2) 其中,Kh(x)=K(x/h)/h,K(x)是有关x的核函数。实际上,f(x|h)可被看做随机变量x+δ的密度,δ是另一个随机变量,其均值为0,密度为Kh(δ).当h是一个较小的值的时候,f(x|h)和f(x)之间的差别实际上可以忽略不计。 (3) 其中,ω(h)在实际中通常是未知的,将ω(h)当作参数向量组中的一个参数加以计算,能有效估计该值的大小。也就是说ω(h) 可用式(4)进行计算: (4) 其中,θ是一个超参数向量,在这种情况下,h的先验表示为ω(h|θ),h的贝叶斯估计表示为h0(x|θ).因为f(x|h)是未知的,任何基于ω(h|θ)的推理或计算都不能直接进行。当从x观察到一个随机样本,表示为{x1,x2,…,xd}时,可以用样本均值来近似描述f(x|h)的值,形式化描述如下: (5) 该值被称为f(x)的核估计量,可以估计x点在数据集D中的密度。 基于局部密度的异常检测,其性能在很大程度上取决于邻域参数k值的选择,只有当k值足够大,使得邻域中的大多数样本保持正常,才能有效检测到离群的数据。为了提高对参数k的鲁棒性影响,特提出一种基于均值的邻域密度。与传统的邻域密度相比,基于均值的邻域密度是领域中所有样本点的局部密度均值,它对邻域中存在的离群数据非常敏感,其形式化定义如下所示: (6) 公式(6)表示样本点x的邻域密度,其中q是样本点x的任一邻居,即它是x的k-距离邻域中一个点。该公式可以看出,k距离越大,样本点的局部密度越小,对于正态样本,其邻域样本大多是正态的,其邻域密度与平均邻域密度相似。但对于一个异常,当参数k很小时,其邻域中异常的比例是不确定的。当样本中有很大一部分是异常邻域中的异常时,邻域密度可能急剧下降,从而影响异常的检测。采用基于均值的局部密度估计,得到的k值范围比传统的邻域密度估计的k值范围宽得多,因此它对k值的变化具有更强的鲁棒性。 离群因子用于估计样本的离群程度,是判断离群数据的重要因素。通常情况下,正常的样本位于稠密区域,比较密集,具有较高的局部密度和邻域密度。相反地,离群数据一般分布在比较稀疏的区域,样本点的局部密度较低,而且样本点与其邻居的距离较远。因此,可以采用样本点的局部密度以及其邻域密度估计作为样本点的离群因子,并用于度量样本点是处于稠密区域还是稀疏区域,从而确定是否属于离群对象。下面公式给出了离群因子Outlier(x)的形式化定义。 (7) 从公式(7)可以看出,样本的局部核密度越小,其邻域的均值密度越大,离群因子越大,样本越可能是离群数据。对于大多数与正常对象分离的离群数据,它们的局部密度与邻域密度相差很大,从而保证了它们的离群因子远大于1.对于数据集中的大多数样本点,它们的局部密度更接近其邻域密度,从而确保其离群因子在1左右波动。这使得区分离群和正常样本数据变得很容易。 考虑到所有样本的离群因素,离群数据的检测方法可有如下两种:1)按离群因子的降序排列的前N个样本视为异常;2)离群因子大于阈值的样本被视为离群,在本文中,采用第一种方法实现离群数据的检测。 基于核密度估计的离群挖掘算法(Outlier Mining based on Dernel Density Estimation,OMDE)总体上分为三步,第一步是确定数据集D中每个对象的k-距离邻域,这一步需要计算两两对象之间的距离,并返回每个对象的k个邻居及其距离;第二步是根据公式(5)计算并估计每个对象的样本点密度,然后根据公式(6)估算每个样本点的邻域密度;最后,根据公式(7)计算每个对象的离群因子,将所有离群因子排序,获取最大的N个值,其对应的数据对象为离群数据。其算法描述如下: 算法: OMDE 输入:数据集D,离群数量N,邻居数量k; 输出:离群数据; 1)for each object x in dataset D 2) dis[]=dis(x,o);//o是除x之外的对象 3) disk(x)=sort(dis[],k); 4) Near[ ] = compute k-nearest neighbors of x 5)end for 6)for(i = 0; i < n; i++) 7) for (j = 0; j < d; j++) 9) end for 11)end for 12)for each object x in dataset D 14) All Outlier(x)are saved to the array fac[]; 15)end for 16)sort(fac[]); 17)return the largest N values in fac[]; 18)end 本节描述了一系列实验并给出了相应的实验分析,主要从准确性和时间的角度将本文提出的算法OMDE与其他最先进的方法进行比较,并分析了参数k和N对OMDE算法性能的影响。 为了有效评价参数对算法OMDE的性能影响,数据集的选择是一个较难解决的问题,为此,我们采用人工合成数据集。具体而言,是采用文献[14]给出的基于分割模型的数据生成方法,生成了不同簇数的合成图,这些合成图聚焦于属性空间的不同子集,包含多个聚簇,并且具有不同的大小范围。总体而言,该数据集和任务是基于密度的离群点检测的经典设置:与聚集图像的成员相比,稀有对象应该位于密度较低的区域。 4.1.1 参数k对算法的影响 在基于k近邻的数据分类以及离群数据挖掘中,参数k对算法有较大的影响,主要体现在对算法效率和准确性的影响。 图2显示了不同的k值对OMDE算法效率的影响,从该图中可以看出,OMDE算法无论采用那种核函数,都会随着k值的增加,其效率降低,即算法执行的时间随着k值的增加而增加。其原因是,当k值增加时,每个样本点计算其k近邻的个数会增加,毫无疑问,这会需要更多的时间代价。另外,在相同的k值下,采用本文提出的核函数比Gaussian和Epanechnikov核函数具有更少的执行时间,这能充分体现本文核函数在离群挖掘中具有更好的性能。 图2 参数k对OMDE算法的效率影响Fig.2 The effect of parameter k on the efficiency 图3显示了不同的k值对OMDE准确性的影响,从该图中能看出,随着k值的增加,算法的准确性明显增加,其原因是当k是一个较大的值的时候,样本点的k近邻的计算更加准确,这更能体现节点之间的不同,从而提高离群数据挖掘的准确性。 图3 参数k对OMDE算法的准确性影响Fig.3 The effect of parameter k on the accuracy of OMDE algorithm 4.1.2 参数N对算法的影响 在OMDE算法中,离群数据的检测是按离群因子的降序排列的前N个样本,因此参数N对算法的性能具有较大的影响。 图4显示了不同的N值对算法OMDE执行时间的影响,从该图可以看出,当N值增加时,无论采用那种核函数,算法的执行时间都将增加,特别地,Epanechnikov核函数同其它两个核函数相比,具有最低的效率。其原因是,当N值增大时,说明需要找出更多的离群点进行输出,这会增加离群检测的开销,导致算法效率降低。 图4 参数N对OMDE算法的效率影响Fig.4 The effect of parameter N on the efficiency of OMDE algorithm 图5是参数N对算法准确性的影响,随着N值的增大,算法的准确性明显增高,这是因为当N是一个大值的时候,离群数据的范围将扩大,真正的离群将更有机会被检测。从图5还能看出,本文提出的核函数的准确性比其它两个核函数的准确性略低,但在N为300时,三个核函数的准确性基本相同,结合图4的算法效率能够得出,本文提出的核函数以微不足道的准确性的降低换取了较高的效率。 图5 参数N对OMDE算法准确性的影响Fig.5 The effect of parameter N on the accuracy of OMDE algorithm 本组实验主要实现相关算法之间的性能比较,为了体现实验的多样性,我们采用下面几组真实数据作为实验的数据集。 The KDD Cup 1999:这是一个用于网络入侵检测研究的通用数据集。在这个数据集中,选取60 593个正常对象和228个标记为离群的对象,每个对象由41个特征属性,这些数据共同构成了KDD数据集,成为算法性能比较的第一组实验数据。 The Mam dataset:该数据集是从乳腺摄影图像数据集中提取的。包括9 923个正常对象和200个离群对象,每个对象具有6个特征属性,Mam数据集,成为算法性能比较的第二组实验数据。 The Ann dataset:这是甲状腺病变的数据集,由3 000个标准对象和50个离群对象构成,每个对象包含21个属性,这是本节的第三组实验数据。 4.2.1 效率比较 在算法效率比较的实验中,将我们算法的OMDE与ADMNC和KEDOS算法进行了比较。ADMNC[14]是一种用于处理具有分类和数值输入变量混合的大规模问题的异常检测算法;而KEDOS[15]是一种基于核密度估计的基于密度的孤立点检测方法,它允许集成领域知识和特定需求,能嵌入在更广泛的离群点检测框架中。图6给出了不同数据集下各个算法的运行时间,该图显示,本文提出的方法OMDE,无论在那个数据集上,其运行时间都最短,充分说明,OMDE算法同ADMNC和KEDOS相比,具有更高的效率。 图6 不同算法效率比较Fig.6 Efficiency comparison of different algorithms 4.2.2 准确性比较 图7是在不同数据集上,算法OMDE与ADMNC和KEDOS的准确性比较。图7显示,在KDD Cup数据集上,我们的方法OMDE同其他两个算法相比,准确性具有非常显著的提高,而在Mam和Ann数据集上,准确性改善的幅度不大。结合图6算法效率的比较,可充分说明,OMDE算法不仅在效率上,而且在精度上,同先进算法ADMNC和KEDOS相比,都有显著改善。 图7 不同算法准确性比较Fig.7 Accuracy comparison of different algorithms 数据集的形态复杂多变,导致不同数据集的密度难以计算,针对这一问题,本文提出了一种基于核密度估计的离群数据挖掘算法OMDE。在定义样本邻域的基础上,结合核密度估计,给出了样本点及其邻域的核函数,并推导了核密度估计的公式及方法,为样本点密度的度量提供了一种有效方法。在此基础上,通过计算离群因子来检测离群数据,从而为离群数据挖掘提供了一种新算法。为了有效适应数据集在量上的急剧膨胀,下一步将重点研究基于核密度估计的并行离群检测算法。
2.2 核密度估计
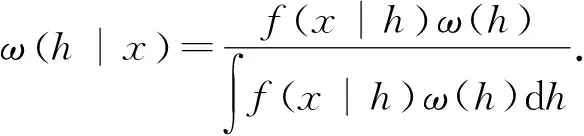

2.3 邻域密度度量
3 离群挖掘与算法描述
3.1 离群因子估计
3.2 算法描述
4 实验与分析
4.1 人工合成数据集




4.2 真实数据集

5 总结
