一种快速确定聚类中心的光谱聚类方法

周永祥，杨海峰，蔡江辉，尚晓群

(太原科技大学 计算机科学与技术学院，太原 030024)

随着技术的发展，先进的天文望远镜能够获取越来越多的光谱数据。在大数据时代的背景下，首要问题便是天文工作者们如何处理海量数据。之前的人眼识别已无法满足这项巨大工程的需求，因此很多工作者们将目光投向了计算机的自动处理。

目前，有很多研究工作都放在天文与计算机结合上，比如：将自动聚类算法[1]应用到星系和恒星分类中，利用神经网络算法[2]对恒星和星系的图像进行分类，结果表明神经网络算法可以很好的运用在恒星和星系图像的分类中。Ball[3]等人利用决策树对光谱数据进行分类并且也取得很好的测试结果。有人利用模糊分类与神经网络算法[4]对非线性数据进行分类，发现模糊分类与神经网络可以很好地处理复杂数据类型。Moore等人[5]运用数学形态学方法对CCD图像进行分类，发现能很好地区分出星系，但是将其应用到恒星中时错分率较高。轨迹聚类应用到光谱的天光分析中[6]，最终取得不错的效果。还有一种聚类也用光谱数据进行了测试[7]，效果也很好。

本文是对LAMOST DR5的光谱数据进行分析处理，主要意图是运用全新的预处理方法对光谱数据进行数据预处理，此预处理方法利用不同恒星光谱数据在不同波段表现性质不同的特点，将特定波段的波形转化为具体的数据，之后计算这些具体数据的密度和距离，通过密度和距离挑选出合适的奇异点，从这些奇异点中选出可靠的聚类中心，最后利用K近邻来生成所有的簇。FDCC是一种独特的聚类中心点快速确定的聚类方法，大多数聚类算法的难点都在于怎么确定中心点，而FDCC能够快速地确定聚类中心点所在，之后，可以直接利用简单的K近邻方法来确定簇，这样可以减少程序运行的时间。

1 相关研究

1.1 LAMOST简介

在本文中，数据集全部来自LAMOST DR5V3，LAMOST[8-9]也被称为郭守敬望远镜，它一次性可拍摄4 000张光谱图像。文中的DR5光谱数据就是LAMOST从2011年十月到2017年六月获取的全部光谱数据，这其中一共包括4 151个区域和9 026 365个光谱数据，并且信噪比大于10的光谱数据达到了7 775 981条。在大视场天文学研究上，郭守敬望远镜是居于国际领先地位的大科学装置。

1.2 聚类技术

科技的发展使得大数据时代来临，在海量数据面前，如何设计好所需的算法极为重要。聚类技术[10]是算法中的一部分，这类技术不同于分类，它无需训练数据来训练模型，直接可以对现实数据进行处理，由于这种特性，这项技术在问世之后得到了飞速的发展。多数聚类算法是使用某种度量方法将数据按照簇间不相似及簇内相似进行划分，当然在很多工作中，聚类也可用于数据预处理，比如聚类算法可用于离散化处理。聚类技术可以被分为四种方向，分别是基于划分，基于层次，基于密度，基于网格。这四种方向都有自己的代表算法，并且对于数据如何聚类都有各自的理论。在基于划分的聚类方法中，K-Means是其代表算法，这种方法多数是使用距离度量，其中欧式距离使用频率最高。并且K-Means有很多变种，分别是利用均值，众数和中心点等等，从而对其中心点的选择进行优化，为了能够处理海量数据，有人对K-Means的分布式算法进行优化设计。基于层次的聚类算法主要分为两种，一种是自底向上的凝聚层次聚类，另一种是自顶向下的分裂层次聚类。这类聚类方向的代表算法有birch,针对初始凝聚和分裂聚类算法死板的缺点，很多论文都研究出如何在分裂和凝聚的过程更好的评估中间过程得到的簇，并且针对这种聚类算法选择好的度量比较困难，对于有缺省值的数据对象也无法很好的处理。基于密度的聚类方法对识别球状分布有很好的效果，这种聚类思想依赖于密度半径和邻域对象个数，其中代表算法是DBSCAN，针对DBSCAN需要设置参数的缺点，提出OPTICS算法对DBSCAN进行改进，这种密度聚类思想对于聚类有很好的效果，并且能识别出多种数据。与以上三种数据驱动形式的聚类方向不同，基于网格的聚类是将数据空间转化为网格的形式，以网格形式上进行聚类操作，主要的代表算法是STING统计信息网格算法。以上就是四种基本的聚类思想，根据其相应理论，经过后人持续的研究，如今已取得很大的成果。

2 聚类算法FDCC

本节将对聚类算法FDCC进行详细描述，在2.1节介绍FDCC的主要思想，并且在2.2节详细介绍FDCC的算法步骤，最终在2.3节中对算法进行理论分析。

2.1 算法的思想

本文的思想主要是首先对天文光谱数据进行预处理实现数据降维，之后利用距离和密度的关系快速找出聚类中心，最后根据聚类中心快速聚类。本文算法FDCC分为两步，第一步对天文光谱数据进行预处理，提取出发射线位置上的置信度信息，这里的提取信息是将发射线区间中的波形变成一个具体的值来表示存在此发射线的置信度，在此文中，给定的发射线都会被用在数据预处理中，在提取出特定发射线的置信度后，第二步计算所有数据的密度和距离，利用密度和距离确定出数据中的奇异点，之后从奇异点中选出合适的聚类中心，最终通过K近邻得出聚类结果。

2.2 FDCC聚类算法描述

本文的算法是分为两步，第一步是数据预处理，数据预处理得出存在此发射线的置信度，发射线存在与否和波长位置，还有波形都有关，一个发射线存在的位置越靠近特定的波长位置时，它就越可靠，并且如果左右两边的波形越对称，它就会更加可靠。在给定特定发射线的波长位置之后，需要在每个发射线的波长位置上确定一个合适的波长区间来提取发射线，此处波长范围需恰当，因为在光谱数据中，很多发射线的波长位置相距较近。因此应避免在提取一条发射线的时候还包含了其他的发射线。有了发射线的波长区间，便可以在这个特定的波长区间中提取发射线存在的置信度。首先找出区间中所有的峰值，如果在发射线波长位置附近没有峰值的存在，那么表明不存在此发射线，此发射线的置信度也被设置为0.一条好的发射线存在的位置应当尽可能地靠近在特定的发射线波长附近，所以当发射线存在的位置越靠近特定发射线波长位置时，它就越可靠。在本阶段，最靠近此发射线位置峰值的波长值与此发射线波长值相减得到的绝对值，将之称为间距，这个间距越小，那么发射线存在的置信度就越高，因此间距的倒数才能用来组成发射线的置信度。接下来需要评判波形的对称性，本阶段需要用到的是左右两边的高度和宽度，分别记录下左右两边的宽度Wl和Wr，之后根据斜率的变化，记录下两边的高度Hl和Hr，之后通过公式1来计算出差异d，公式(1)如下：

(1)

差异d越小，表明存在此发射线的置信度越高，因此差异d的倒数才能组成发射线置信度。因此，在整个预处理过程中，间距的倒数和差异d的倒数共同组成这个发射线的置信度，置信度将变成一个具体的值。在整个数据预处理的过程中，全部发射线均需进行上述提取过程，将这些给定的发射线分别变成一个具体的数值。每条天文光谱数据在经过数据预处理后，都会变成相对低维的数据，这样实现了数据降维。本身的光谱数据具有几千维，经过数据预处理后，数据变成了几十维的数据，大大减少了后续聚类过程的运行时间。

在完成数据预处理阶段之后，第二步需要对数据进行聚类处理，即进入到下一个聚类阶段，此阶段的主要思想是中心点的密度和距离与其他点不同，聚类中心点应当是密度高且相互距离远，噪声点与之不同，它的特点是距离远但密度低，较于其他的点，它们不属于任何一个簇且密度较低。首先算法计算所有点之间的距离，得出一个距离矩阵，并且初始化密度半径阈值dc，根据距离矩阵和dc，利用公式(2)可得到每个点的密度。

ρi=∑f(dij-dc)

(2)

(3)

得到每个点的密度之后，再根据每个点的密度计算每个点的距离。文中的距离是只计算与比本身密度大的点之间的距离，利用公式(3)可以得到距离。

δi=min(dij)(ρj≥ρi)

(4)

对于密度最大的点，它的距离就是距离矩阵中最远的距离。最后每个点都将自己的距离和密度相乘得到一个新的变量γ.通过新的变量γ来选出符合条件的奇异点，假设γ的分布是一种正态分布，大部分正常的点都会落在区间(μ-5σ,μ+5σ)，落在区间外的点就会被判定为奇异点。得到这些奇异点后，还需要进一步排除掉奇异点中的伪中心点。真正中心点的距离和密度应当不会相差过大，根据这一假设可以将伪中心点全部排除，之后剩下的就是聚类中心点。得到这些中心点之后，再利用k近邻来得到聚类中所有的簇。算法的伪代码如下所示：

算法1 FDCC(Fast Determination of Clustering Center)

输入：数据A；中心点个数K；百分比percent；调整幅度r

输出：聚类的簇C

For给定发射线do 提取发射线的置信度

IF发射线波长位置附近有峰值的存在then

dis =abs(最靠近此发射线位置峰值的波长值-此发射线波长值)

记录下左右两边的宽度Wl和Wr

记录下两边的高度Hl和Hr

计算所有数据的距离得出距离矩阵mat_dis,最大距离max_dis，最小距离min_dis

While r > 0

For i in range(2)

If i==0

dc=min_dis+(max_dis-min_dis)*((percent-r)/100)

If i == 1

dc=min_dis + (max_dis-min_dis)*((percent + r)/100)

根据公式(2)，dc和距离矩阵mat_dis计算每个点ρi

根据公式(3)，ρi计算距离δi

γ=ρi×δi

根据γ选出奇异点，根据奇异点的距离和密度找出中心点center

Iflen(center)==K

使用K近邻得到所有的簇

Fitness1=mean(所有簇的簇内距离)

Fitness2=mean(所有簇的簇间距离)

C=fitness最大时得到的簇

2.3 算法分析

在此算法中，算法预处理对数据进行降维，这大大减少了算法所需要的时间和空间，并且本算法的时间复杂度是○(nlogN)，算法的增长趋势并不快，再加上降维处理，使得算法本身实际的时间复杂度要低于理论上的时间复杂度。因为数据预处理进行了降维，这也降低了空间复杂度。本文聚类算法中密度半径阈值dc极为重要，为了能够找出最好的密度半径阈值dc，算法使用爬山法来找密度半径阈值dc，检验这个密度半径阈值dc好坏的思想是簇间距离大，簇内距离小，因此可以根据簇间和簇内距离计算出此密度半径阈值dc的fitness，通过fitness和爬山法选出最好的密度半径阈值dc，并且得到最好的聚类形成的簇和聚类中心点，这样就能保证聚类结果的质量。

3 实验分析

3.1 实验方案

本次实验环境是WINDOWS 10操作系统，Intel(R)Core(TM)i7-6700HQ的CPU和8.0GB内存。本阶段实验从三个方面评估FDCC：准确率、召回率和运行效率。

本次实验使用的是LAMOST DR5中的恒星数据，经过精心挑选而得到五个数据集，五个数据集的数量分别是2 000，8 000，16 000，18 000，20 000.每个数据集只有A类和K类恒星数据，并且每类都各占一半,具体可从表1中查看。在挑选发射线的时候，我们选择了13条发射线，分别是：H_delta：4101.734；H_beta：4861.325；OIII_4959：4958.911；OIII_5007：5006.843；Hel_5876：5875.67；OI_6300：6300.304；NII_6548：6548.040；H_alpha：6562.800；NII_6584：6583.460；SII_6717：6716.440；Ca_K：3933.66；Ca_H：3968.45；Na_D：5891.94.该算法的预处理过程将这13条发射线变成具体的置信度来进行聚类。

对于聚类算法初始化，需要提前给出中心点个数k，爬山法中开始的百分比percent和百分比左右调整的幅度r.这里k初始化为2，因为只有两类数据，产生出来的也只有两个聚类中心点。开始的百分比percent初始化为15，百分比左右调整的幅度r初始化为3.对于对比算法，本文实验选了四种聚类算法，分别是DJ-Cluster[11]，hierCluster，K-Means和DBSCAN.这四种聚类算法将分别用到上述的五个数据集中，得到四类算法的准确率，召回率和时间，将之与本文中的聚类算法进行比较。

3.2 准确率分析

本文针对不同量级的光谱数据集，对FDCC算法以及四种同类算法进行了准确率对比实验，实验结果如表2所示，其准确率的对比柱状图如图1所示。

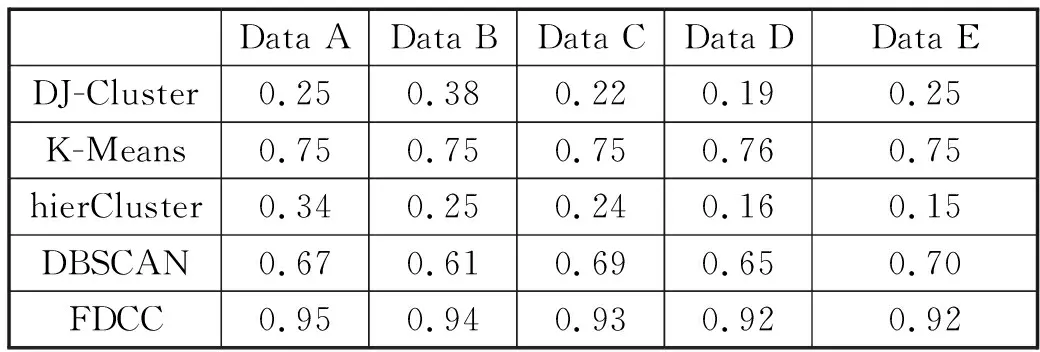
表2 五种算法在五种数据集下的准确率Tab.2 Accuracy of five algorithms on five data sets

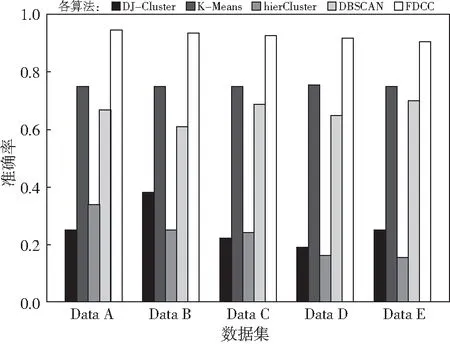
图1 同类算法的准确率比较分析Fig.1 Accuracy analysis of five algorithms under five different data sets

从图1的柱状图中可以看出虽然随着数据量的增加，本文聚类算法的准确率有着下降的趋势，但是趋势很小，并且在数据量达到一定数量的情况下，这种下降的趋势在慢慢消失，可以从灰色柱状来查看FDCC算法的准确率，可以看到在测试到Data D的时候，算法的准确率就开始保持平稳，虽然有着微弱的下降，但是下降的趋势已经在消失，并且从表2中也可以看到Data D和Data E的准确率在约去小数点后两位数之后已经保持一致。

从图1中看出，其他对比算法的准确率并不会出现较大的差异。DJ-Cluster和hierCluster算法一直保持着较低的准确率，这两类算法无法正确的对光谱数据进行聚类，聚类出来得簇会出现较多或者较少得情况。K-Means和DBSCAN这两类算法的准确率一直都处于中等水平。这两类算法对于簇的个数划分准确。但是划分中也会出现错误，因而准确率不会很高。本文聚类算法CCFD对簇的划分是准确的，并且两个簇中的数据也很少有错误的划分结果。具体的准确率信息都呈现在表2中，并且图1也用柱状图表现出来。

3.3 召回率分析

图2和表3反映了算法在五种数据集下的召回率，从五种算法的对比中可以看出CCFD在召回率上依旧保持最高，虽然在Data A,B,C，D下，召回率有所下降，但是当数据量达到18 000到20 000的时候，CCFD的召回率已经开始不下降了，并且保持了平稳状态。因为数据量的增加，使得情况变得复杂，特殊数据就会增加，在这种情况下，有一些特殊数据无法被分到正确的簇中，召回率就会有所下降，但是大数据量达到一定程度的时候，这些特殊数据的数量也会保持稳定，结果就会保持平稳。从表2中可以看出召回率在整个数据集实验中都是比较接近的，这说明几乎所有的数据都会被分到一个簇中，并且大部分的数据都会被分对，而我们挑选的数据都是属于两个簇的，这也符合数据情况。而且错分的个数都比较少，因而可以达到这种高效果。但是其他对比算法没有这种高效果。

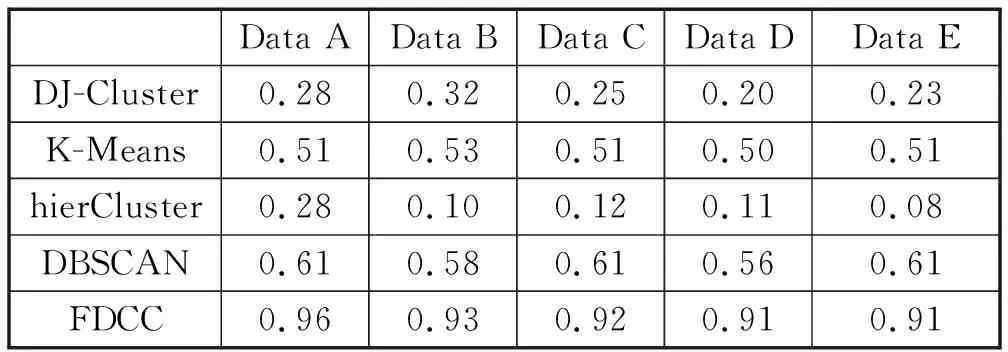
表3 五种算法在五种数据集下的召回率Tab.3 Recall rate of five algorithms on five data sets

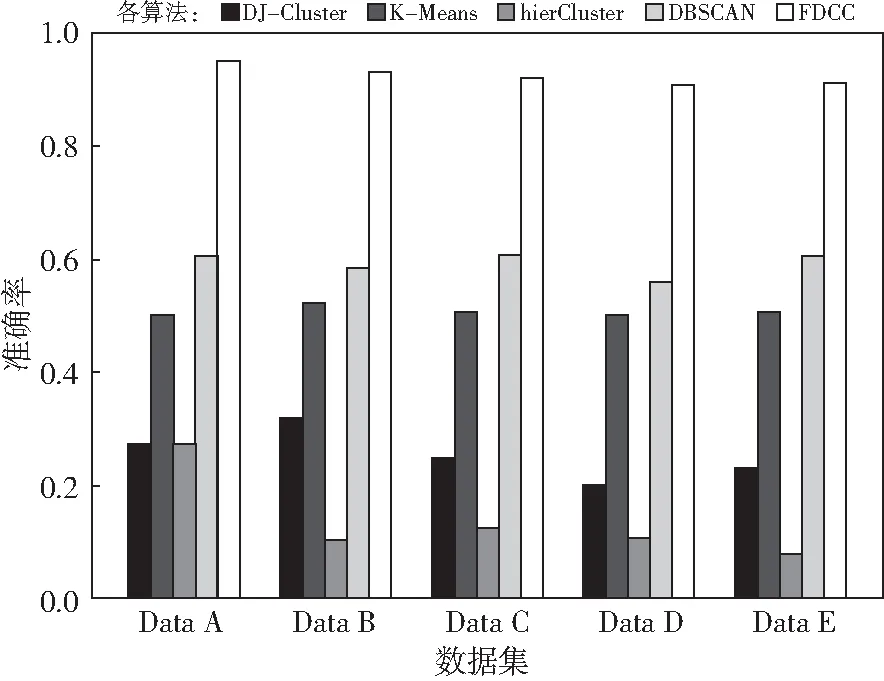
图2 同类算法的召回率分析Fig.2 Recall rate analysis of five algorithms under five different data sets

从图2对比算法中来看，各对比算法对光谱数据处理的结果都比不上FDCC，这是因为每个对比算法都是处理三千多维数据，这种高维数据进行的聚类，必然会有很多维度来影响聚类的结果。其他对比算法中都分成了不止两个簇，因而其他对比算法的效果都是比较不理想。从图2中可以看出DJ-Cluster和hierCluster此两种聚类不适合这种高维光谱数据，它们都会将数据分成好几个簇，得到的结果很差，因而召回率必然都会很低。

3.4 运行效率

图3说明了五种算法的运行时间，在图3中分别测试了Data A,C,E，数据量分别是2 000，16 000和20 000，在三种数据集中，Data A中只有DJ-Cluster有着较长的运行时间，并且它在其他两种数据集中也有着很长的运行时间，其余四种算法在Data A下运行时间都相差不大，没有比较大的差异，这可能是数据量很小，算法在处理速度上无法展现出较大的差异。在Data C下，五种算法就开始表现出各自的差异，DJ-Cluster的运行效率依旧是最低，运行时间是最长的。而hierCluster的运行时间排在了第二位中，但是相较于DJ-Cluster，hierCluster的运行时间是比较短的。之后便是DBSCAN，K-Means和本文聚类算法。K-Means和本文聚类算法在时间上的差异很小，本文聚类算法比K-Means要低一点。虽然两种聚类算法在运行时间上差不多，但是在这种运行时间下，本文聚类算法的准确率和召回率都是比较高的，要远远地优于K-Means.从Data E中来看，五种算法都可以看出差异的大小，此时由于算法的缘故，DJ-Cluster依然有很长的运行时间，hierCluster和DBSCAN也有明显的运行时间差异，很明显，hierCluster聚类算法有较长的运行时间，在Data E下，K-Means的运行时间依然要高于本文聚类算法一点。从整体上来看，本文中的聚类算法相较于其他算法在光谱数据上的表现依旧有很好的性能。

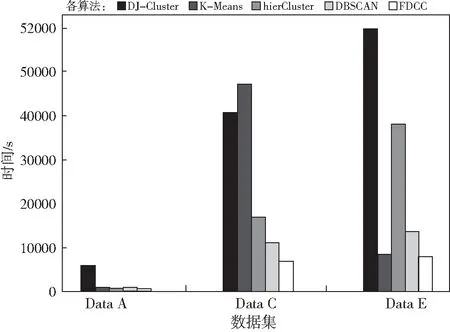
图3 同类算法的运行效率分析Fig.3 Time efficiency of five algorithms under three data sets

本文聚类算法识别的部分光谱如图4和图5所示。本文在比较这部分工作中分别选取了A类和K类恒星聚类中心点、三个边缘点，从光谱图像中可以看出A和K类中心点都具备各自恒星光谱的特征，但是这些边缘点的特征是很难识别出来的，这也符合聚类结果的特点，中心点数据比边缘点数据具备着更加明显的特征。

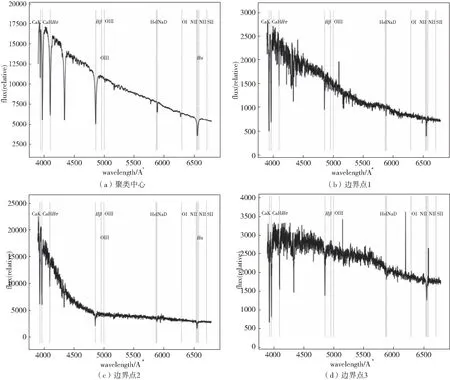
图4 A型恒星光谱数据Fig.4 Spectral data of class A-type star

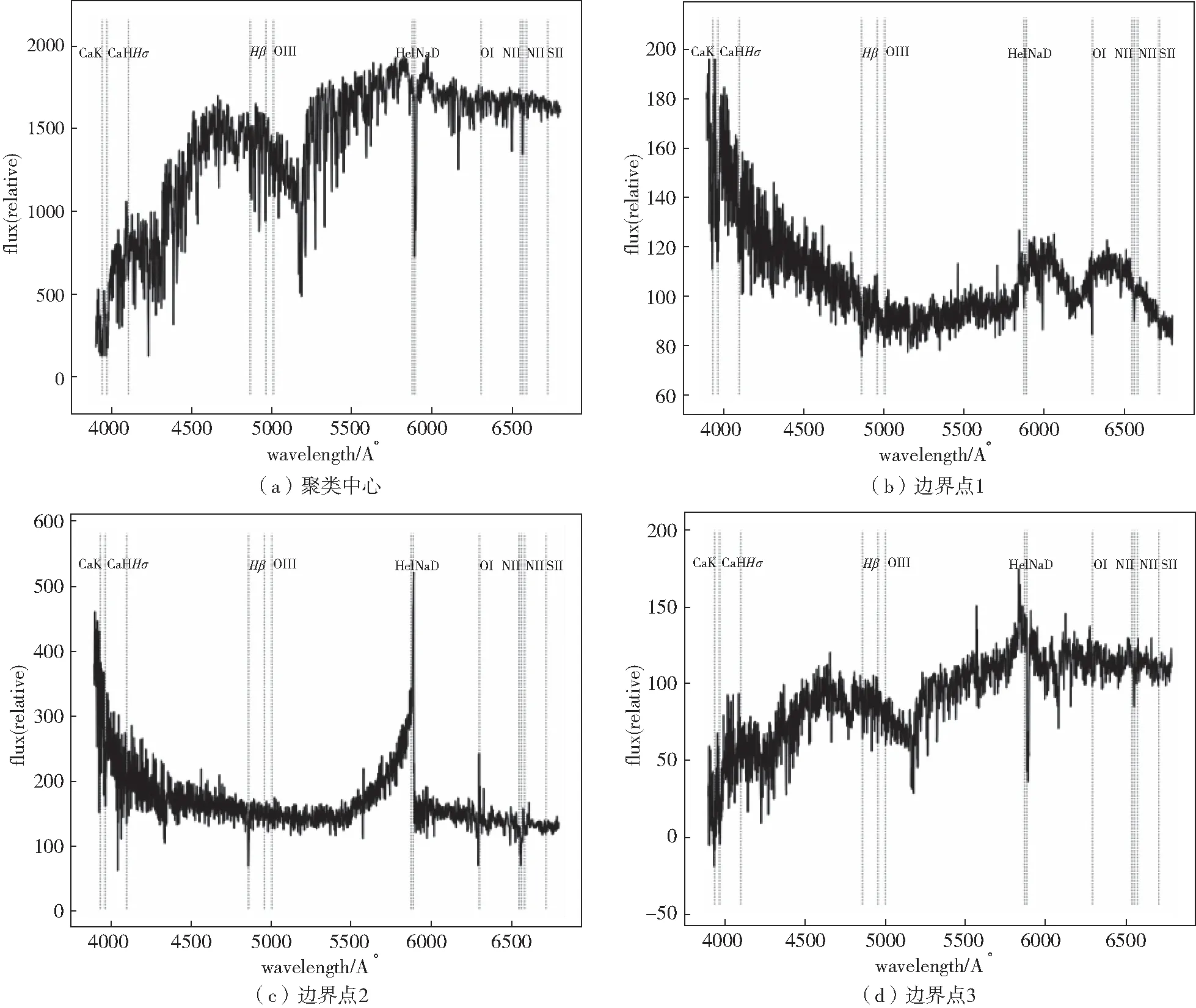
图5 K类恒星光谱数据Fig.5 Spectral data of class K-type star

4 结论

本文对恒星光谱数据的聚类算法进行研究,并且提出了一种快速确定聚类中心的光谱聚类方法(FDCC).恒星光谱数据通常都是高维数据，具有很高的复杂度，为克服这种困难，本文提出了对光谱发射线进行数据预处理来对数据进行降维，之后利用密度和距离快速的确定聚类中心点，最后利用中心点和K近邻算法来找出所有的簇。文中通过实验将之与其他聚类算法对比，得到的结果表明FDCC可以运用到光谱数据中。对于更多种类和更多数量的恒星数据，需要在后续研究中进一步解决。