函数零点应用问题的热门考点剖析

王玉新

函数零点应用问题是高考的常考点。下面就常见考点，举例分析，供大家学习与参考。

考点一：应用函数零点求取值范围

解答这类问题，如果题设中有关于函数零点的条件，就不能把函数零点看成一个概念，而应该抓住零点与函数图像的特征以及零点存在的判断条件，从而达到函数零点的解题功效。

对于0＜x1＜x0，f x1( )的值恒为正值，即f x1( )的取值范围是0，+∞( )。

当函数具有单一的单调性，而又存在零点时，则在这个零点的左右两侧的函数值异号，即在这个零点的左右两侧函数值恒为正或恒为负。本题的解答正是抓住了这一点，解决了函数值f x1( )的取值范围。

考点二：应用二分法求函数的零点或方程的近似解

给定精度ε，用二分法求函数f(x)的零点近似值的步骤如下：第1 步，确定区间[a，b]，验证f(a)·f(b)＜0，给定精度ε；第2步，求区间(a，b)的中点x1；第3 步，计算f(x1)，①若f(x1)=0，则x1就是函数的零点，②若f(a)·f(x1)＜0，则令b=x1(此时零点x0∈(a，x1))，③若f(x1)·f(b)＜0，则令a=x1(此时零点x0∈(x1，b))；第4步，判断是否达到精度ε，即若|a-b|＜ε，则得到零点值a(或b)，否则重复步骤2～4。

例2 用二分法求方程ln(2x+6)+2=3x在区间(1，2)内的近似解(精确到0.1)。

解：原方程可化为ln(2x+6)-3x+2=0。令f(x)=ln(2x+6)-3x+2，用计算器得到如表1所示的对应值。

表1

观察表中对应值，可知零点在(1，2)内。

取区间中点x1=1.5，由f(1.5)≈-1.00＜0，可知零点在(1，1.5)内；再取区间中点x2=1.25，由f(1.25)≈0.20＞0，可知零点在(1.25，1.5)内。

同理取区间中点 x3= 1.375，由f(1.375)≈-0.39＜0，可知零点在(1.25，1.375)内；取区间中点x4=1.3125，由f(1.3125)≈-0.074＜0，可知零点在(1.25，1.3125)内。

由于区间(1.25，1.3125)内任一值精确到0.1后都是1.3，故方程ln(2x+6)+2=3x在区间(1，2)内的近似解是1.3。

解答这类问题的关键是要确定零点所在的大致区间。所求的区间长度应尽量小，否则会增加运算次数和运算量。解题时应注意运算的准确性，也应注意对精确度的要求。本题充分展示了利用二分法求方程近似解的过程，同时使同学们学会了借助精度终止二分法的过程。

考点三：二分法在经济技术中的应用

市场经济价格自行调整，若供过于求，价格会跌落，若供不应求，价格会上涨，找一个价格平衡点，应怎样找? 不妨试着求一下。

例3某农贸市场出售的西红柿，当价格上涨时，供给量相应增加，而需求量相应减少，具体调查结果如表2，表3所示。

表2_

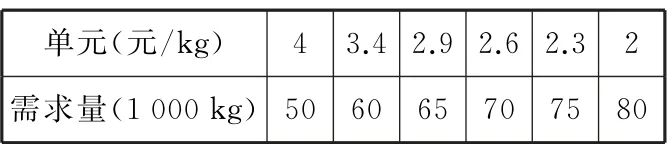
表3

据以上提供的信息，市场供需平衡点(即供给量和需求量相等时的单价)应在区间( )。

A.(2.3，2.6) B.(2.4，2.6)

C.(2.6，2.8) D.(2.4，2.8)

解：A 中供给量在(50，70)之间，需求量在(70，75)之间，供给量不足，排除A，B 中的供给量不足。易知D 中的供给量也不足。应选C。

或者，建立直角坐标系，以横坐标表示供给量(需求量)，纵坐标表示价格，利用所给数据在坐标系内描点，画出供给量线和需求量线(折线)，即拟合曲线，供给量线和需求量线的交点即为市场供需平衡点(图略)。从图中可以看出市场供需平衡点应在(2.6，2.8)内。

充分阅读题目，理解题意，把两表中的信息与题目要求结合起来，可找答案。利用数形结合的思想方法处理本题也是一个不错的解法。