时间-速率双因素下全尾砂膏体的屈服应力易变行为

李翠平，颜丙恒✉，王少勇，侯贺子，陈格仲

1) 北京科技大学土木与资源工程学院，北京 100083 2) 金属矿山高效开采与安全教育部重点实验室，北京 100083

全尾砂膏体具有“不分层”、“不离析”、“不脱水”的优良工程特性，可有效提高矿产资源的回采率及生产安全性，实现废弃尾矿资源的再利用，解决地表尾矿库安全隐患与环境污染，具有显著的环保、安全优势[1]. 膏体充填流程中，浓密环节耙架扭矩[2]、管道输送阻力[3-4]和膏体堆积坡度[5]是全尾砂膏体制备需要解算的重要工艺参数，而屈服应力被认为是解算工艺参数的重要流变参考依据.

对于全尾砂膏体，学术界目前多视其为理想屈服应力流体，如Bingham流体、H-B流体和Casson流体等[6]，认为屈服应力是判定膏体料浆能否发生流动的临界剪切应力值[7]. 以理想H-B流体为例，全尾砂膏体所受剪切应力小于屈服应力τy时，膏体料浆保持静止，大于屈服应力时膏体料浆发生流动，即屈服应力是固态-流态转换时的一个转折点. 基于理想屈服应力流体观点，张连富等[8]研究了膏体料浆浓度与屈服应力之间的演化规律，张钦礼等[9]为预测全尾砂膏体料浆浓度-屈服应力建立了改进BP神经网络；刘晓辉等[10]以固体填充率为量化指标，综合分析了全尾砂膏体体积分数、尾矿粒径、尾矿不均匀系数等因素，构建了屈服应力关于固体填充率的计算模型；程海勇等[11]以膏体稳定系数来表征不同矿山充填材料之间颗粒级配的差异性，构建了全尾砂膏体屈服应力预测模型. 可见，以上研究多将膏体屈服应力视为料浆的材料函数，分析料浆本身材料配比差异对屈服应力的影响. 开展屈服应力测量实验的核心观点是，一定配比条件的充填料浆存在唯一与之相对应的屈服应力值，在理想屈服应力流体框架内，认为全尾砂膏体屈服应力是料浆本身固有的一个物理属性值.

然而，近年对胶体悬浮液、软玻璃类材料等屈服应力流体开展的流变物理学研究发现，在由固态至流态转变的过程中，发生了黏度分叉[12-13]、负斜率流动[14]和剪切条带[15]等复杂流变现象，表明其固-流转化过程是不连续的、具有固态与流态共存的流变行为[16-17]. 负斜率流动与剪切条带的出现进一步表明固-流转化过程无法获取稳定的流动曲线[18]，只有大于临界剪切速率时才会获取稳定流动曲线[19]. 因此，不稳定流动现象表明理想屈服应力流体框架内定义的固态-流态连续转换假设已不再成立，此时精准测量屈服应力是非常困难的[20]. 全尾砂膏体颗粒体系分布是多尺度的[6,11]，并且浓密后的全尾砂膏体具有高浓度特性. 多尺度、高浓度膏体内部颗粒间的相互作用复杂，颗粒间彼此接触形成具有一定强度的三维网络结构，网络结构的生成与破坏过程使全尾砂膏体表现出一定的触变性[21]. 因此，全尾砂膏体是否属于理想屈服应力流体，膏体屈服应力是否只受料浆材料配比的影响，需要开展深入的流变实验分析.

为此，本文从全尾砂膏体屈服应力测量实验入手，基于实验数据分析料浆不同测量速率与测量时间下峰值屈服应力、动态屈服应力与静态屈服应力间的变化规律，进而从细观层面分析测量速率与测量时间对膏体屈服应力的影响机理.

1 实验设计

1.1 实验材料与仪器

1.1.1 实验材料

选取某铁矿全尾砂作为本次实验材料，为确定全尾砂膏体适宜浓度范围，首先采用0.1 r·min-1的恒定小剪切测量法（如下文1.2.2所述）估算不同浓度水平下膏体料浆屈服应力的大致范围，测量64%、66%、68%、70%、72%、74%、76%，7种不同质量分数的全尾砂膏体料浆，其屈服应力分别为30.76、70.78、95.37、172.17、313.87、625.74、1344.94 Pa.质量分数64%的料浆屈服应力过小，在测量时出现了严重的泌水分层现象，不满足膏体的“三不”工程特性，质量分数76%的料浆屈服应力过大，料浆丧失了流动性，在充填现场难以进行泵送作业.在满足全尾砂膏体“三不”工程特性以及可流动性的基础上，本次实验全尾砂料浆质量分数依次设为66%、68%、70%、72%、74%共5个水平. 实验所用全尾砂密度ρ=2710 kg·m-3，其粒径分布曲线，如图1所示. 由图1可知，-20 μm细尾矿颗粒占比32.0%，+100 μm粗尾矿颗粒占比10.1%，样品中粗、细颗粒同时存在，粒级分布是多尺度的. 细颗粒之间由于胶体相互作用易形成三维网络结构而产生触变性[21]，粗颗粒之间易发生碰撞与摩擦等接触作用[22].

图1 全尾砂粒径分布曲线Fig.1 Particle size distribution of unclassified tailings

1.1.2 实验仪器

全尾砂膏体颗粒体系的多尺度特性，使其在屈服应力测量时应避免测量前对料浆内部三维网络结构的破坏、以及转子表面与颗粒间的滑移[23-24]，本实验采用桨式转子开展流变测量，为避免粗颗粒在测量过程中发生颗粒迁移而降低测量数据的准确性[25]，采用宽间隙测量系统，测量系统尺寸参数见表1.

表1 桨式转子测量系统尺寸参数Table 1 Size parameters of vane rotor measurement systems

1.2 实验原理与方案

1.2.1 实验原理

基于理想屈服应力流体观点，全尾砂膏体的流变模型常以2参数Bingham流体、Casson流体或3参数H-B流体来表示，3种流变模型均属于理想屈服应力流体，其流变模型如式（1）：

式中：τ为剪切应力，Pa；τy为屈服应力，Pa；k为稠度系数，Pa·sn；ηc为塑性黏度，Pa·s；n为流动指数，量纲为1；为剪切速率，s-1. 分析三种流变模型可知，Bingham流体为H-B流体在流动指数n=1时的特殊形式，此时稠度系数k即为塑性黏度ηc，二者量纲相同，而Casson流体为Bingham流体开方后的特殊形式. 三种流变模型均可由H-B流变模型统一描述，均存在屈服应力τy项，并且三种流变模型对屈服条件的定义均是相同的[7]. 不失一般性，本文以3参数HB流体为例进行分析，所得结论同样适用于Bingham流体与Casson流体. H-B流体屈服应力定义为固态-流态转换时的一个转折点，如式（2）所示：

为得到屈服应力τy，最直接的方法是控制剪切速率逐渐递减至0. 由式（1）的单调递增性可知，剪切应力正比于剪切速率. 维持施加的剪切速率不变，式（1）定义的剪切应力将保持恒定. 理想屈服应力流体框架内，不同剪切速率条件下，剪切应力随测量时间的演化曲线如图2所示.

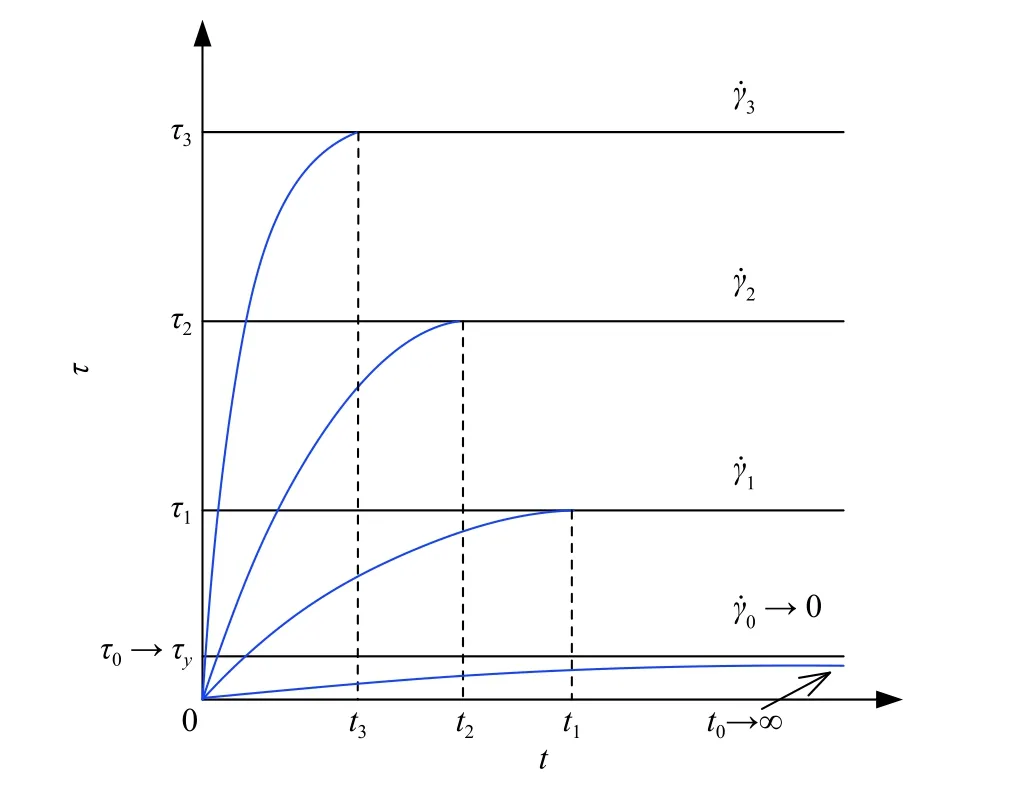
图2 理想屈服应力流体剪切应力-测量时间演化曲线Fig.2 Diagram of evolution of shear stress - measuring time for ideal yield stress fluid

对于理想屈服应力流体，可施加非常小的恒定剪切速率使其逐步逼近0，获取待测的屈服应力[26]，这是依据流变模型式（1）与式（2）定义实施的屈服应力测量方法. 除此之外，还可以逐步递增剪切应力，观测膏体料浆的剪切速率是否由0发生突变[27]，突变点对应的剪切应力即为屈服应力.

综上，基于理想屈服应力流体框架，无论是施加非常小的恒定剪切速率测量方法，还是逐步递增剪切应力测量方法，其测取的屈服应力应是相同的. 因为理想屈服应力流体框架内，膏体料浆在一定的材料配比下，屈服应力是料浆本身固有的物理属性值，其为料浆固态-流态转换过程中一个确定的临界剪切应力值.

1.2.2 实验方案

依据上述理论分析，设计实验方案如下.

（1）恒定小剪切速率法.

设置7种不同的剪切速率，保证转子施加的恒定小剪切速率逐步逼近0. 为研究恒定小剪切速率下，剪切应力-测量时间的演化规律，持续测量600 s，实验参数如表2.

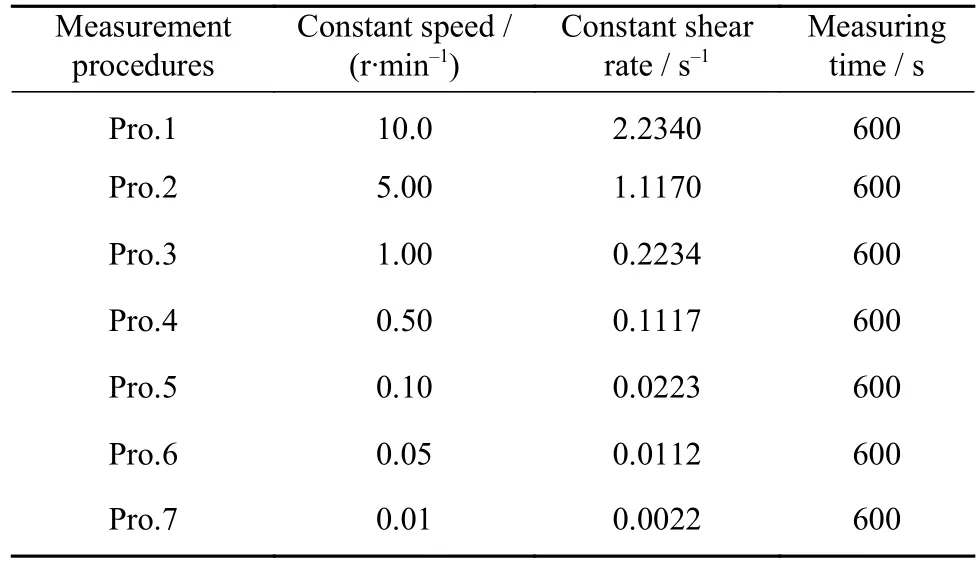
表 2 恒定小剪切速率法实验参数Table 2 Experimental parameters of constant small shear rate method

（2）递增剪切应力法.

设置6种不同剪切应力递增梯度，使剪切应力从0开始逐步逼近屈服应力. 实验参数如表3.

表 3 连续递增剪切应力法实验参数Table 3 Experimental parameters of continuously increasing shear stress method

2 实验结果与分析

2.1 膏体峰值屈服应力易变行为分析

依照表2中的实验程序，开展5种质量分数膏体恒定小剪切速率峰值屈服应力测量实验，以68%质量分数料浆为例，其剪切应力与测量时间的演化曲线如图3所示.

由图3（a）可知，68%质量分数全尾砂膏体在0.0022、0.0112、0.0223和0.1117 s-1四种恒定小剪切速率下，随测量时间的增加依次经历剪切应力递增的黏弹性区域、峰值屈服点、剪切应力递减的应力松弛区. 与图2理想屈服应力流体黏弹区之后恒定不变的剪切应力曲线不同，在超过峰值屈服点之后，剪切应力逐步降低并趋近平衡，进入应力松弛区. 由图3（b）可见，0.2234、1.1170和2.2340 s-1三种恒定剪切速率下，图3（a）中剪切应力递增的黏弹区消失，只存留峰值屈服点以及剪切应力递减的应力松弛区，随剪切时间延长剪切应力-时间曲线趋近平衡.

将5种质量分数膏体料浆在不同剪切速率下的峰值屈服点、以及达到峰值屈服点的时间求出，绘图如4所示，膏体峰值屈服应力记为y1. 由图4（a）可知，对应5种不同质量分数的全尾砂膏体，随恒定剪切速率增加，峰值屈服应力逐步增大；由图4（b）可知，达到峰值屈服应力所需时间逐步降低. 相同剪切速率条件下的峰值屈服应力，随全尾砂膏体质量分数的增加而增大，这与前人的研究结果一致[8-10]. 可见，采用恒定小剪切速率获取的膏体峰值屈服应力不是恒定的，正比于施加的恒定剪切速率值. 并且达到峰值屈服点之后具有剪切应力松弛行为，与理想屈服应力流体框架下剪切应力恒定假设不相同.

2.2 膏体动态、静态屈服应力易变行为分析

2.2.1 动态屈服应力分析

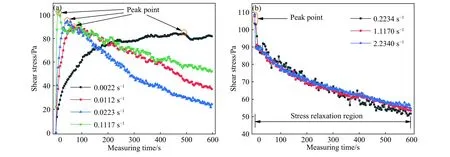
图3 68%质量分数膏体剪切应力-测量时间演化曲线. （a）剪切速率为0.0022、0.0112、0.0223和0.1117 s-1；（b）剪切速率为0.2234、1.1170和2.2340 s-1Fig.3 Shear stress-time evolution curves of pastes with 68% mass fraction: (a) shear rates are 0.0022, 0.0112, 0.0223 and 0.1117 s-1; (b) shear rates are 0.2234, 1.1170 and 2.2340 s-1

图4 小剪切速率下不同质量分数膏体峰值屈服应力与对应时间. （a）峰值屈服应力；（b）峰值屈服应力对应时间Fig.4 Peak yield stress and corresponding time of paste with different mass fractions at small shear rate: (a) peak yield stress of paste; (b) corresponding time of peak yield stress for paste

全尾砂膏体受外界剪切作用后发生流动，撤去外界剪切作用后料浆由流态回归固态时对应的剪切应力称之为动态屈服应力，相反在受到递增剪切应力后由固态转为流态时对应的临界剪切应力称为静态屈服应力[28]. 动态屈服应力是流态转固态条件下测量的，一般多采用拟合回归不同剪切速率下对应的剪切应力求出[27]. 以图3中68%质量分数膏体料浆为例，以7种不同剪切速率下所得剪切应力-测量时间曲线为基础，分别绘制测量时间1、61、121、181、241、301、361、421、481和541 s时的剪切应力-剪切速率曲线，如图5所示.

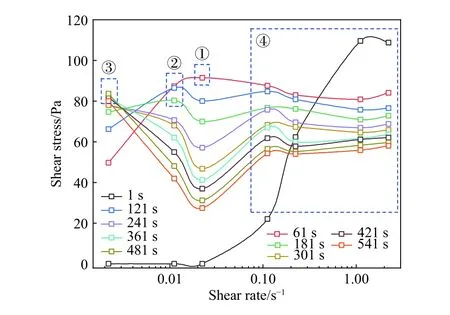
图5 68%质量分数膏体不同测量时间下剪切应力-剪切速率曲线Fig.5 Shear stress-shear rate curves of paste with 68% mass fraction at different measuring times

由图5可知，全尾砂膏体在不同测量时间下剪切应力-剪切速率曲线变化趋势是复杂的，1 s时剪切应力-剪切速率曲线与其他时刻差异最大. 结合图3可知，全尾砂膏体黏弹性剪切应力递增区域，随剪切速率增大而逐步减小直至变为峰值屈服应力点. 因此图5中对应低剪切速率下，1 s时所得剪切应力处于黏弹性剪切应力递增区域，其剪切应力值偏低. 图5中对应较高剪切速率下，1 s时剪切应力处于峰值屈服点处，所得剪切应力值较高. 故1 s时刻受黏弹性影响较为明显与其他时刻剪切应力-剪切速率曲线差异较大. 图5中，61、121、181 s曲线，随测量时间增加，受黏弹性剪切应力递增区域影响逐渐降低，剪切应力-剪切速率曲线峰值点逐渐左移，如图中标记数字①、②. 随测量时间进一步增加，剩下时刻的剪切应力-剪切速率曲线完全去除了黏弹性区域的影响，在最小剪切速率0.0022 s-1处便已经达到了峰值点，如图中所标记数字③，类似于图3中高剪切速率下，黏弹性区域消失直接达到峰值屈服应力的行为. 料浆在较小的剪切速率下，内部结构恢复速率大于结构破坏速率，触变恢复能力较强[13,20]，随剪切速率增加内部结构破坏程度进一步加强，剪切作用强于恢复作用，膏体剪切应力-剪切速率呈现出一定范围的负斜率曲线[29]. 此区域剪切应力-剪切速率受触变性影响较为明显，此时的负斜率现象由料浆本身触变性引起. 之后随剪切速率进一步增大，全尾砂膏体料浆流动过程中黏性阻力增大，对应图3（a）中，0.1117 s-1恒定小剪切速率条件下，超过峰值点后剪切应力-测量时间曲线下降幅度较0.0223 s-1要低，测量中黏性阻力所占比重逐步增加，剪切应力-剪切速率曲线由负斜率缓慢恢复至正斜率，进入稳定流动区域.

综上，获取全尾砂膏体动态屈服应力，可对稳定区域内的数据进行拟合处理，如图5中所示蓝色方框④内剪切应力-剪切速率曲线，避免极低剪切速率条件下，黏弹性、触变性造成的影响. 对应5种不同质量分数的全尾砂膏体，动态屈服应力随测量时间变化规律如图6所示.

图6 不同质量分数膏体动态屈服应力-测量时间曲线Fig.6 Dynamic yield stress-measuring time curves of paste with different mass fractions

由图6可知，各质量分数全尾砂膏体动态屈服应力均随测量时间的增加而逐渐降低. 5种浓度下所得动态屈服应力记为y2，其与测量时间之间的拟合方程如图6中所标记，可发现质量分数越高，拟合曲线斜率越小，即动态屈服应力随时间降幅越大.

2.2.2 静态屈服应力分析

依照表3中的实验程序，以68%质量分数的全尾砂膏体为例，连续递增剪切应力条件下，剪切应力-剪切速率演化曲线如图7所示.

依据全尾砂膏体固态至流态转变时静态屈服应力定义，图7中剪切速率突变区对应的剪切应力值变化幅度很小. 低于突变区对应的剪切应力时，全尾砂膏体处于固态弹性变形阶段，高于突变区对应的剪切应力时，全尾砂膏体处于剪切流动状态，因此剪切速率突变区处于固态-流态转换之间的过渡区域. 在突变区内，剪切应力变化幅值较小，基本可以视为恒定值，即为膏体静态屈服应力[27,29].5种质量分数下，对应6种剪切应力递增梯度所得静态屈服应力如图8所示. 可知，全尾砂膏体静态屈服应力随质量分数增高而增大，对应不同剪切应力递增梯度，静态屈服应力随递增梯度增加而增大.所得静态屈服应力记为y3，其与剪切应力递增梯度的拟合方程如图8中所标记，可发现质量分数越高，拟合曲线斜率越大，即静态屈服应力增幅越大.

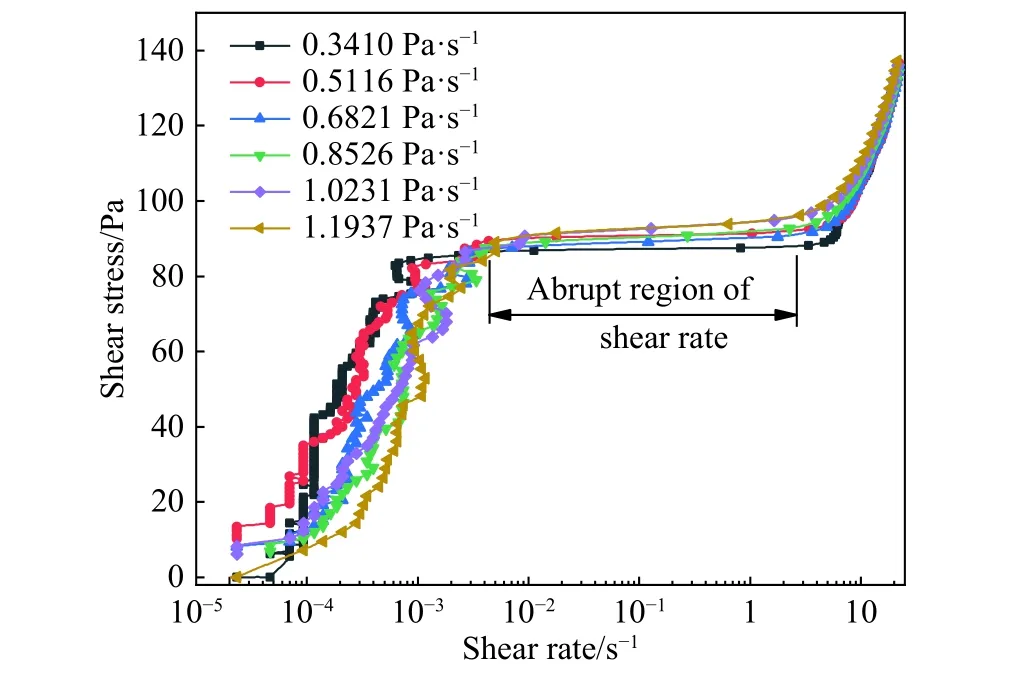
图7 68%质量分数膏体不同剪切应力递增梯度下剪切应力-剪切速率曲线Fig.7 Shear stress-shear rate curves of paste with 68% mass fraction at different shear stress gradients

综上，恒定小剪切速率下的峰值屈服应力y1、不同测量时间下的动态屈服应力y2、不同剪切应力递增梯度下的静态屈服应力y3，在不同测量速率或测量时间下，均呈现出一定的变化规律. 5种质量分数膏体料浆，在3种测量方式与相应测量参数下，共计15个统计组. 单一统计组内，可以变化幅度描述此组数据的离散程度，不同统计组之间为消除测量尺度与量纲对料浆屈服应力离散程度的影响，以变异系数（Coefficient of variation,Cv）评价屈服应力的离散程度，其计算如式（3）所示：

图8 不同剪切应力递增梯度下各质量分数膏体静态屈服应力Fig.8 Static yield stress of paste with different mass fractions at different shear stress gradients

式中：Cv为变异系数，量纲为1；σ为统计组内样本标准差，Pa；μ为统计组内样本平均值，Pa. 15组统计数据如表4所示.

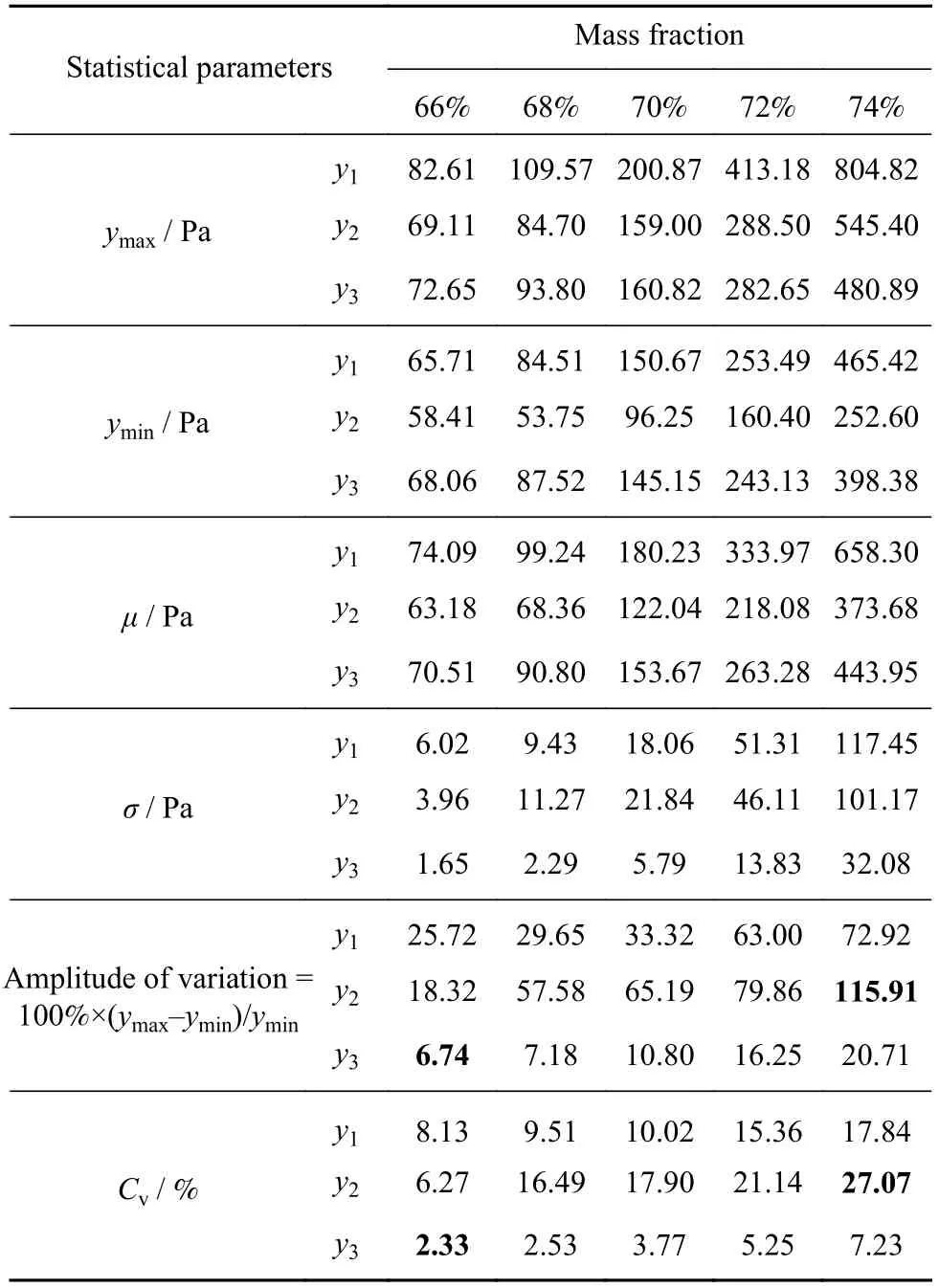
表 4 屈服应力测量实验统计参数Table 4 Statistical parameters of yield stresses measurement

由表4可知，峰值屈服应力y1、动态屈服应力y2，在5种质量分数下，其变化幅度与变异系数均较大. 其中动态屈服应力在74%浓度时最大，变化幅度达到了115.91%，变异系数27.07%. 比较发现，静态屈服应力y3离散程度较小，其在66%质量分数时最小，变化幅度6.74%，变异系数2.33%.5种质量分数下，静态屈服应力在3种测量方法中，其变异系数均是最小的，既静态屈服应力离散程度最小. 同时可以发现y1、y2、y3其随质量分数增加，平均值、变化幅度、变异系数均逐步递增.实际生产中，膏体深锥浓密机内耙架转速恒定，对应恒定剪切速率，耙架对底部料浆的扭矩计算问题需考虑峰值屈服应力；管道稳定输送时断面内剪切速率沿管径方向变化，计算管输阻力时需考虑动态屈服应力；管道停泵重启时对应固态向流态的转变，计算泵的重启压力需要考虑静态屈服应力. 因此对应不同膏体充填工艺环节，在计算工程问题时需考虑三种膏体料浆屈服应力的易变行为.

3 细观机理分析

以上实验结果表明，屈服应力受不同测量过程的影响，而这一现象可通过分析膏体料浆细观层面力学机理予以解释. 全尾砂膏体料浆，具有颗粒多尺度、高浓度两个特性. 在此条件下，细观颗粒之间相互作用力包含：布朗作用力、胶体作用力、流体动力学作用力、接触作用力[30]. 对测量屈服应力而言，其在较低剪切速率条件下，可忽略颗粒间接触作用力. 图1中，粒径小于1 μm的尾矿颗粒占比较低，而较大粒径尾矿颗粒受布朗作用力较弱，可忽略布朗作用力[31]. 此时，所测的屈服应力主要受胶体作用力与流体动力学作用力的影响. 静止条件下，料浆细观颗粒结构如图9（a）所示，假设颗粒直径为2r，局部范围内颗粒间平均距离为b，料浆受到外界扰动作用F，其等效为外界施加的应力扰动或应变扰动. 对于胶体作用力，其涉及多种影响因素，如颗粒表面双电层结构、分子之间的范德华力、以及絮凝剂表面化学效应等.

静止状态下，可将胶体作用力对颗粒的限制等效为一个势阱[21,30]，即颗粒在其中受到胶体作用力限制，难以离开其位置，如图9（a）中颗粒1，记局部范围颗粒体系势垒为Φ. 扰动作用下，流体动力学作用力主要考虑为黏性阻力FH，由斯托克斯公式（4），可得：

图9 膏体料浆细观颗粒结构模型与屈服过程示意图. （a）细观颗粒结构模型；（b）屈服过程示意图Fig.9 Diagram of mesoscopic particle structure model of paste and yield process: (a) mesoscopic particle structure model; (b) diagram of yield process

式中：η为膏体料浆黏度，Pa·s；Vr为所移动颗粒相对于临近颗粒的速度，Vr=，m·s-1；为受扰后料浆内有效剪切速率，s-1. 颗粒1运动至1’位置时，逃出势阱限制范围可视为局部颗粒体系的屈服过程，如图9（b）所示，此时局部范围颗粒体系势垒为Φ’. 颗粒1运动至1’的屈服过程中，在主要考虑流体动力学作用力、胶体作用力的条件下，外界施加扰动过程所消耗的能量主要包含两个部分[22]：克服流体动力学作用力（黏性阻力）所做的功WH，以及两种状态下的势垒差ΔΦ，计算所耗能量如式（5）：

式中：E、WH、ΔΦ单位均为焦耳（J）. 在颗粒1迁移至1’的屈服过程中，外界扰动下颗粒为逃离势阱需要发生迁移运动，此时需要额外克服黏性阻力所做的功. 同理，全尾砂膏体料浆在流变测量过程中，无论哪一种屈服应力以及相应的测量手段，都不可避免的会在料浆屈服前额外克服黏性阻力所做的功，而此部分功正比于测量时对料浆所施加的扰动程度（正比于剪切速率与剪切应力）. 因此，y1、y3在测量过程中施加的扰动程度越大，其需要克服的黏性阻力功越大，对应流变仪需要施加较大的扭矩，即获得较大的屈服应力值. 若想获取准确的屈服应力，即颗粒1需要克服的势阱ΔΦ，需要在没有外界扰动的情况下进行测量，但实际测量中是难以实现的. 为此，需要在尽量小的扰动条件下进行屈服应力测量. 对比y1、y3测量过程可知，采用恒定小剪切速率（y1），相比于递增剪切应力（y3）测量方法，前者是在控制剪切速率模式下开展的，扰动颗粒运动的程度远高于y3控制剪切应力的方法. 因此表4中，在5种质量分数下，y1、y3两种测量过程中，y3的变化幅度与变异系数均是最低的.

至于动态屈服应力y2，其对应不同测量时间，拟合图5中的④区域数据获取的. 此区域颗粒结构恢复速率远小于破坏速率，随时间增加，料浆内细观颗粒结构进一步破坏如图10所示.

膏体料浆这种细观结构随时间而演变的性质正是其触变性的体现. 图10中，假设料浆在持续剪切条件下，局部范围内颗粒数目不变（即质量分数保持不变）. 随剪切破坏过程局部范围内颗粒结构发生破坏与重组，以相邻两颗粒接触数评价局部颗粒体系势垒的强弱. 对应不同剪切时间：t0、t1、t2，图10中颗粒接触数分别为：42、41、40，屈服过程中需要迁移的颗粒数目分别为：7、6、5. 随剪切过程持续，颗粒结构发生变化，由较高的势垒结构逐渐降低，即Φ0＞Φ1＞Φ2. 结合式（4），ΔΦ逐渐降低，因此测量屈服应力时消耗的能量逐渐降低，表现出动态屈服应力y2随时间增加而逐渐降低. 动态屈服应力逐渐降低的过程，亦是膏体料浆结构发生变化而引起的触变性体现.

4 结论

（1）恒定小剪切速率法下峰值屈服应力y1受剪切速率的影响，峰值屈服点正比于施加的恒定剪切速率；恒定剪切速率测量过程中，黏弹性剪切应力递增区域随剪切速率的增大而逐渐减小.

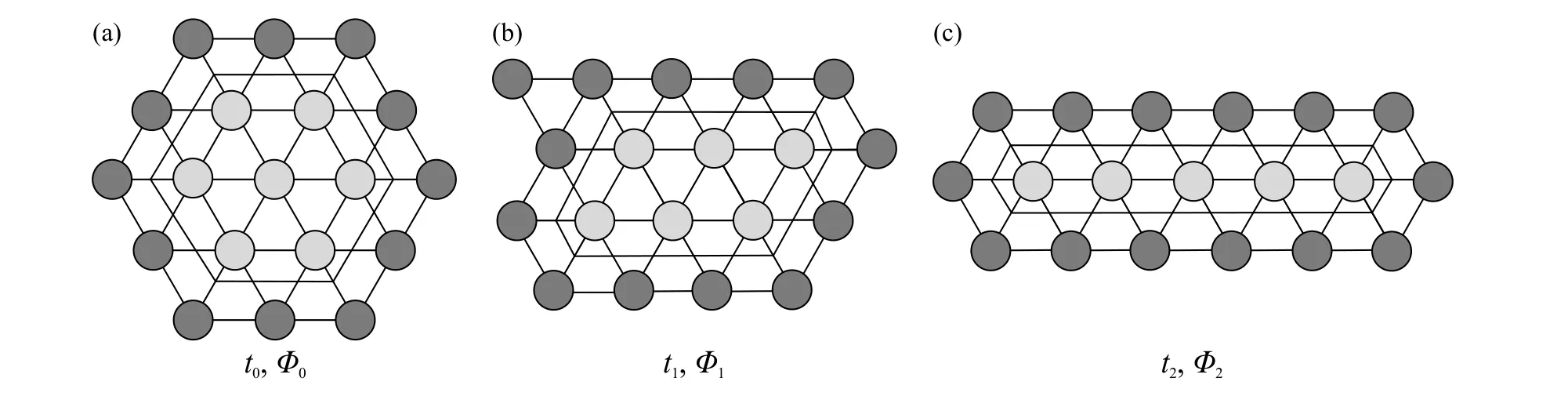
图10 膏体料浆细观颗粒结构随时间演化示意图. （a） t0时刻细观颗粒结构；（b） t1时刻细观颗粒结构；（c） t2时刻细观颗粒结构Fig.10 Diagram of mesoscopic particle structure evolution with time of paste: (a) mesoscopic particle structure at t0; (b) mesoscopic particle structure at t1; (c) mesoscopic particle structure at t2

（2）不同测量时间下动态屈服应力y2不相同，动态屈服应力随测量时间的增加而逐步降低. 质量分数越高，其降幅越大；静态屈服应力y3随剪切应力递增梯度的增加而逐步增大. 质量分数越高，其增幅越大.

（3）3种屈服应力随质量分数的增高均增大，随质量分数增高，其变化幅度与变异系数均逐渐增高，74%浓度料浆动态屈服应力对应最大变化幅度115.91%、最大变异系数27.07%；相比之下静态屈服应力y3受流变测量过程的影响最小.

（4）膏体料浆细观层面机理分析表明，y1、y3测量过程中的易变行为主要源于扰动过程中的流体动力学作用，屈服应力受测量过程影响；膏体动态屈服应力y2易变行为主要源于料浆结构改变引起的触变性.