基于扩散度的尾砂膏体流变特性
2020-11-03陈鑫政杨小聪郭利杰许文远魏晓明
陈鑫政,杨小聪,郭利杰✉,许文远,魏晓明
1) 矿冶科技集团有限公司,北京 102628 2) 国家金属矿绿色开采国际联合研究中心,北京 102628
膏体充填因具有“一废治两害”、充填体质量好、作业环境优等优点在国内外矿山得到广泛应用,也是实现绿色开采的主要技术[1-4]. 膏体的流变特性是影响膏体充填管道设计的重要因素. 膏体属于非牛顿结构流体,在管道中呈柱塞状整体移动,通常视为宾汉姆(Bingham)体,其流动特性可通过测定流变参数(屈服应力和黏度系数)表征[5-7]. 在充填实践中,通常采用测定坍落度的方式衡量膏体的流动特性[8-11],该方法借鉴于混凝土行业标准[12].使用上下直径分别为100 mm和200 mm,高为300 mm的锥形筒,将膏体分三层装入,测定拔起后筒高与坍落后膏体最高点之间的高度差. 然而尾砂膏体与混凝土在料浆含水率、骨料粒径和工况条件等方面具有较大差别,矿山生产实践表明,混凝土行业标准中测定坍落度方法并不适用于尾砂膏体.与混凝土相比,尾砂膏体的流动性更大,骨料粒径极细,坍落度测试不仅费时、费料,而且所测结果无法区分不同配比膏体的流动性. 沈慧明等[13]研究了7.5 cm小型圆柱与标准锥形坍落度的对应关系,认为小型圆柱法可作为测定细粒级膏体坍落度的一种新方法. 田世文等[14]在研究超大流动度混凝土中引入了扩散度表征流动性的参数. 《普通混凝土拌合物性能试验方法标准》(GB T50080—2016)[12]中说明当混凝土拌合物的坍落度大于220 mm时,需开展混凝土扩展度的测定. 《混凝土外加剂匀质性试验方法》(GB T8077—2016)[15]中通过测试流动度表征水泥净浆的流动性.
结合尾砂膏体物料特性,本文借鉴水泥净浆流动度的测试方法,引入扩散度参数,通过开展室内试验,研究质量分数、灰砂比对尾砂膏体扩散度的影响,利用Brookfield R/S桨式流变仪测试膏体的屈服应力和黏度系数,分析扩散度与屈服应力和黏度系数的关系,并根据5个矿山的试验数据,构建尾砂膏体的屈服应力与扩散度的经验模型,以期为矿山充填现场提供一种简便、可靠的测试膏体流变特性的方法.
1 尾砂膏体扩散度测试
1.1 扩散度测试方法
参照《混凝土外加剂匀质性试验方法》(GB T8077—2016)测试水泥净浆流动度的试验方法[15],采用上口直径为36 mm,下口直径为60 mm,高度为60 mm的内壁光滑无接缝的金属截锥圆模测试尾砂膏体的扩散度. 搅拌均匀的尾砂膏体注入截锥圆模内,用刮刀刮平,将截锥圆模按垂直方向提起,时间控制在3~5 s;读取尾砂膏体流淌部分互相垂直的两个方向的最大直径,取平均值作为尾砂膏体的扩散度,试验装置如图1所示.
1.2 截锥圆模内物料受力分析
锥形坍落筒提起前后的应力分布如图2所示.在坍落筒任一水平位置的应力为其上物料的自重应力,坍落筒提起后,物料在剪切应力下发生变形流动,在屈服区域上方,重力引起的最大剪应力低于屈服应力,该区域物料保持未屈服状态. 假设屈服物料与未屈服物料之间的分界是一个水平面,且该水平面在物料坍落的过程中向下运动,则最终坍落高度可根据未屈服高度(h0)和已屈服高度(h1)得到.
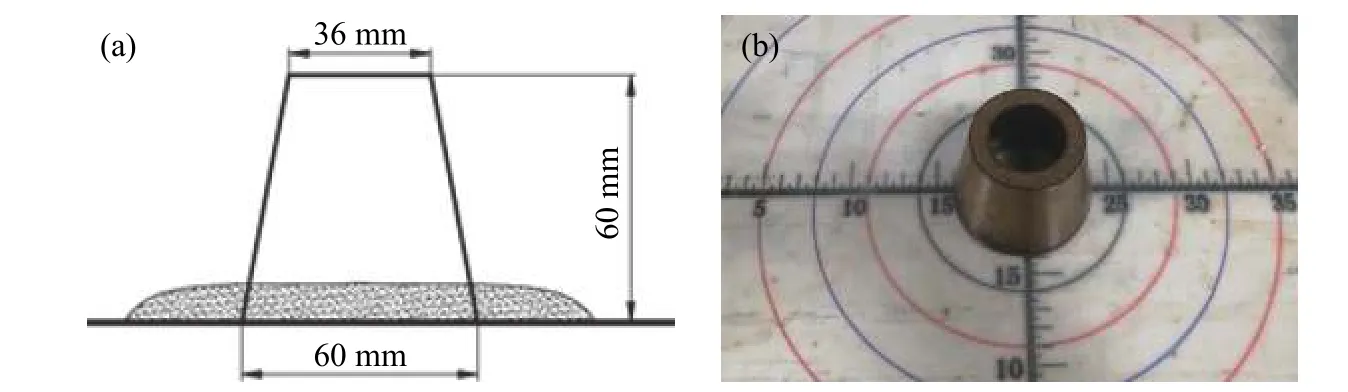
图1 扩散度试验装置. (a)示意图;(b)实物图Fig.1 Device of spread test: (a) schematic diagram; (b) physical image
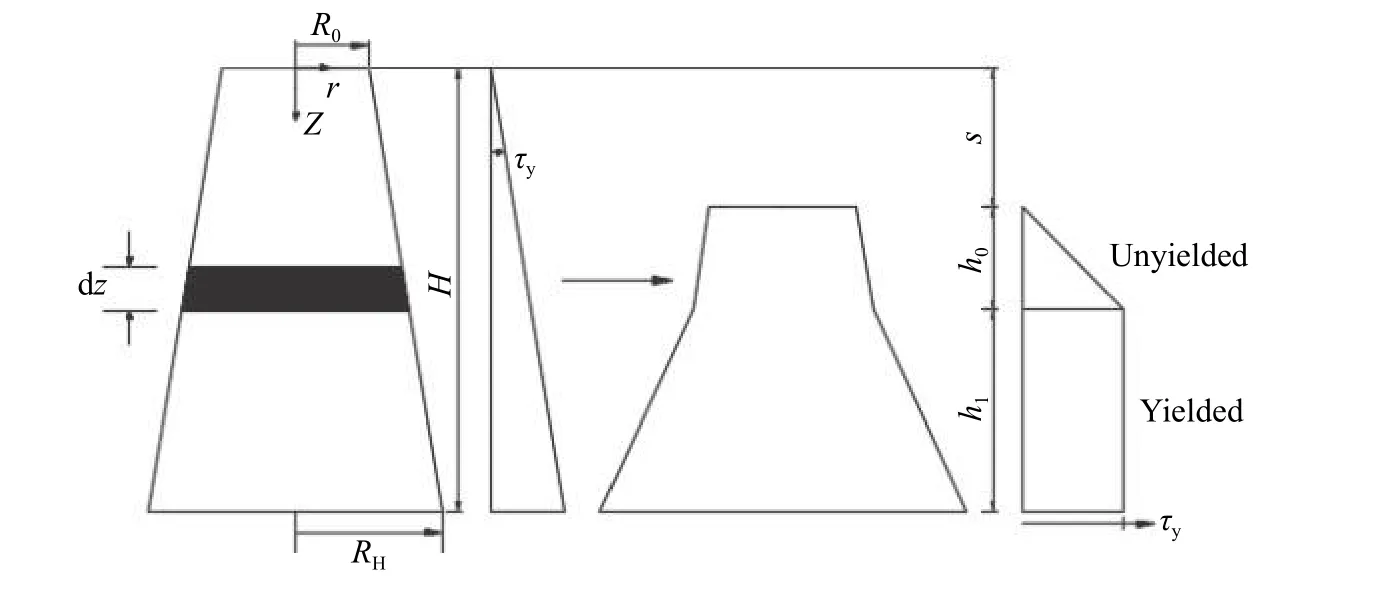
图2 坍落筒提起后前后应力的变化Fig.2 Schematic diagram of the conical slump test, showing initial and final stress distributions
其中,R0为坍落筒的上部半径,m;RH为坍落筒的底部半径,m;H为未变形物料的初始高度,m;r为坍落的物料上部半径,m;z为坍落范围内某一高度,m;dz为z处物料的厚度,m;τy为物料的屈服应力,Pa;s为物料的坍落度,m;h0为未屈服物料的高度,m;h1为屈服物料的高度,m.
根据文献[11],距离筒顶z水平的最大剪切应力量纲为一后的结果可见式(1).

其中,α=R0/(RH-R0);τz′为距筒顶z处最大剪切应力量纲一的值,等于τz/(ρgH);z′为高度的量纲一的值,等于z/H.
未屈服区域h0水平的最大剪切应力即是物料的屈服应力,由式(1)可得:

其中,τy′为物料的屈服应力量纲一值,等于τy/(ρgH);h0′为未屈服区域高度h0的量纲一的值,等于h0/H.
假定物料为不可压缩,屈服区域高度h1由下式(3)可得:
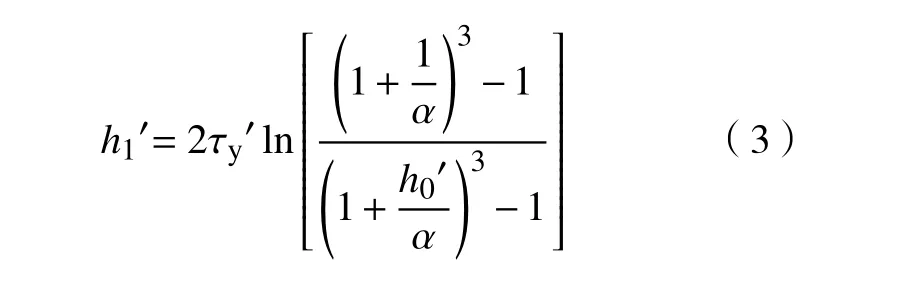
其中,h1′为屈服区域高度h1的量纲一的值,等于h1/H.
量纲为一后的坍落度(s′)可以表示为:
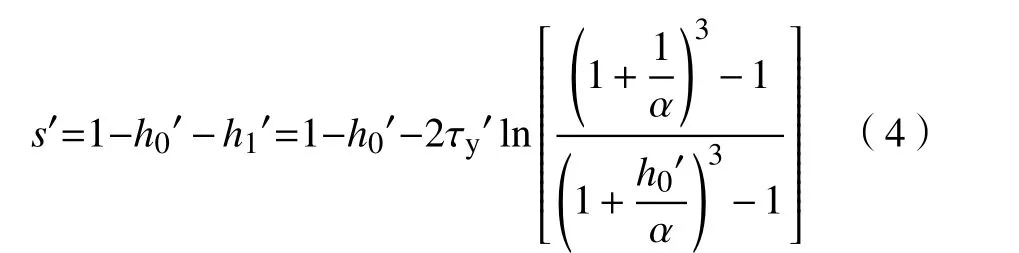
假定尾砂膏体为不可压缩浆体,截锥圆模拔起后浆体向四周呈圆饼状均匀流动,如图3所示,则浆体扩散度与坍落度的关系为:
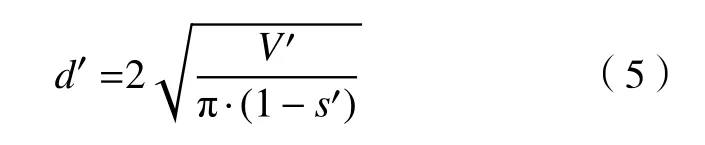
其中,d′为扩散度的量纲一的值,等于d/H;d为物料的扩散度,m;V′为截锥圆模体积的量纲一的值,等于V/H3;V为截锥圆模的体积,m3.
联立式(2)~式(5),可以得出量纲为一化后的扩散度与屈服应力的关系,式(6)可看作扩散度与屈服应力的解析模型,但该式太过复杂不利于指导矿山充填.
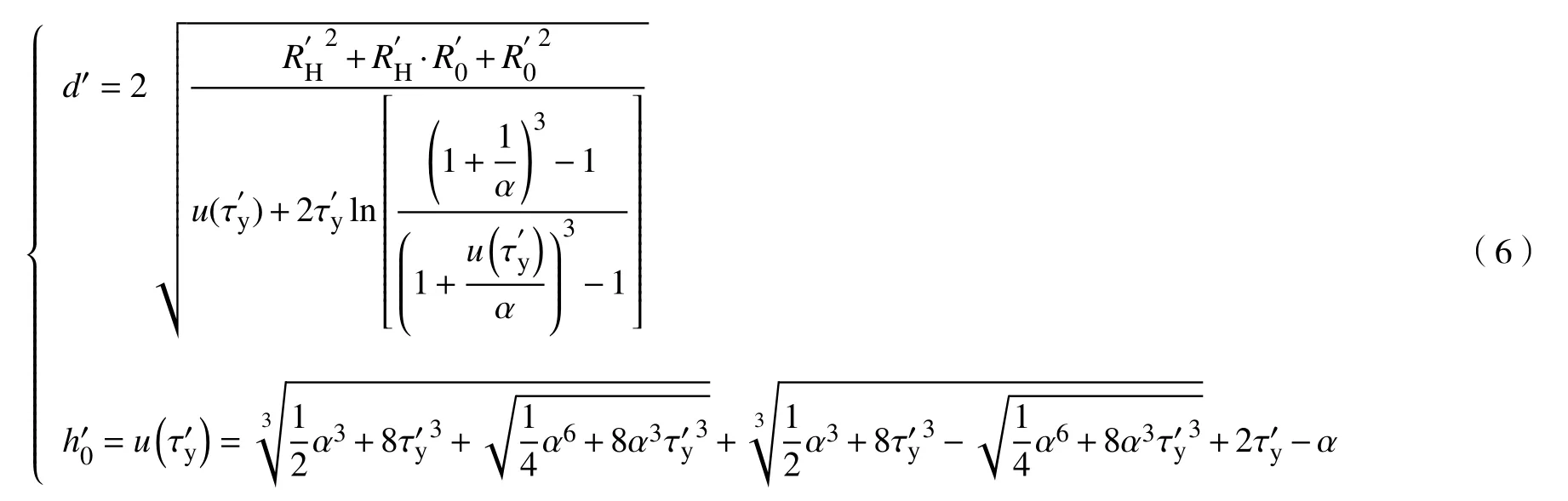
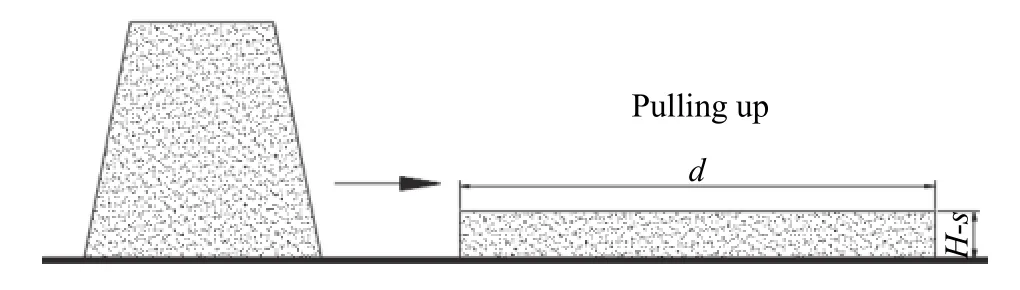
图3 扩散度测试示意图Fig.3 Schematic diagram of spread test
其中,RH′为RH的量纲一的值,等于RH/H;R0′为R0的量纲一的值,等于R0/H.
2 试验
2.1 试验材料
本文选择5个矿山的尾砂开展扩散度与流变参数测试试验,胶凝材料为P.C 32.5级水泥,实验用水为实验室自来水. 按照《土工试验方法标准》(GB/T50123—1999)测定相对密度和自然堆积密度,采用马尔文激光粒度分析仪测试尾砂的粒径分布,结果如表1所示,尾砂的粒径分布曲线如图4所示.

表1 尾砂的物理参数Table 1 Physical parameters of tailings

图4 尾砂粒径分布曲线Fig.4 Particle size distribution of tailings
2.2 试验方案
以云南某多金属矿尾砂为例,采用全面试验设计方法,膏体质量分数选择68%、70%和72%,每个质量分数对应5个灰砂比,分别为1∶4、1∶6、1∶8、1∶10和1∶20,按照扩散度试验方法测试膏体的扩散度,并利用R/S桨式流变仪测试屈服应力和黏度系数[16-18],如图5所示.
3 试验结果与分析
3.1 试验结果
按照试验方案开展试验,每组平行开展2次试验取均值,扩散度和流变参数测试结果如表2所示,图6为灰砂比为1∶10,质量分数为68%、70%和72%的尾砂膏体扩散度测试结果.

图5 R/S桨式流变仪Fig.5 R/S paddle rheometer
3.2 扩散度与尾砂膏体配比的关系
图7(a)为不同灰砂比条件下,尾砂膏体扩散度随质量分数的变化曲线,图7(b)为不同质量分数条件下,尾砂膏体扩散度随灰砂比的变化曲线.由图7(a)可知,扩散度随质量分数的增加呈显著减小趋势,灰砂比为1∶4、1∶6、1∶8、1∶10和1∶20条件下,质量分数为68%和72%的尾砂膏体扩散度的差值分别为8.75、7.10、7.95、7.45和8.40 cm. 由图7(b)可知,扩散度随灰砂比的减小无明显变化,不同质量分数下亦无相同的变化趋势,质量分数为68%、70%和72%条件下,5个灰砂比的扩散度极差分别为1.45、0.70和0.60 cm.
利用SPSS统计分析软件,开展双因素方差分析[19-20],显著性水平α=0.05,结果如表3所示. 其中,sig.,df,F分别是显著性(P值),自由度,方差检验量(回归方程的显著性检验). 由表3可知,质量分数和灰砂比对尾砂膏体扩散度的处理效应(R Squared)为0.991,即除质量分数和灰砂比两因素以外,随机误差仅为0.009. 灰砂比对尾砂膏体扩散度影响不显著(sig.=0.577>0.05),质量分数显著地影响尾砂膏体扩散度(sig.=0.000),由此可判断尾砂膏体的扩散度主要受质量分数因素影响,可忽略灰砂比对尾砂膏体扩散度的影响.
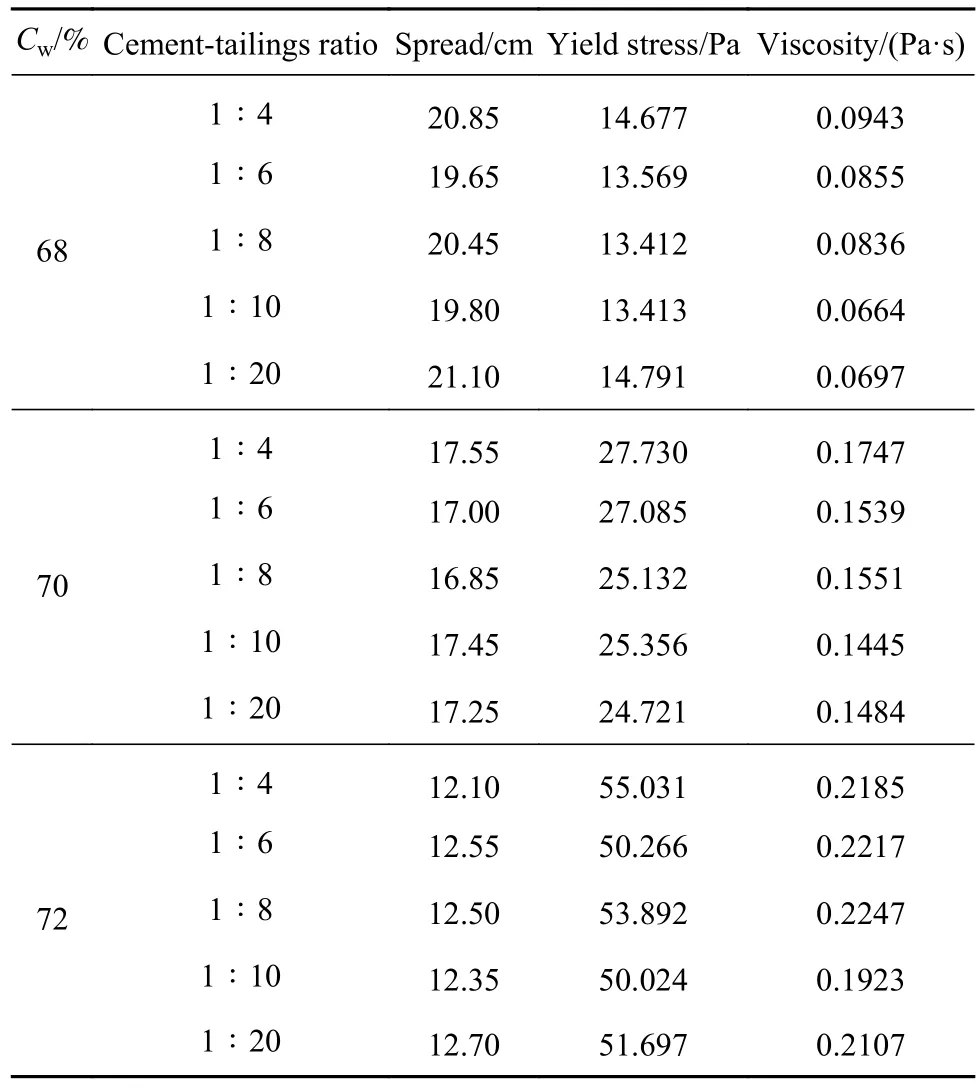
表 2 尾砂膏体扩散度和流变参数测试结果Table 2 Results of spread and rheological parameters test of tailings backfill paste
3.3 扩散度与流变参数的关系
图8(a)和图8(b)分别为尾砂膏体扩散度随屈服应力和黏度系数的变化,由图8可知,尾砂膏体的扩散度随屈服应力和黏度系数的增加而减小,即扩散度随尾砂膏体流动性变差而减小,且尾砂膏体扩散度的变化规律与其屈服应力及黏度系数的变化趋势相吻合,这说明扩散度能直观反映尾砂膏体的流动特性.
3.4 经验模型构建与验证
3.4.1 经验模型构建
上述试验表明尾砂膏体的扩散度与其流变参数具有相同的变化趋势,结合其他2个矿山(印尼某铅锌矿和新疆某铜矿)试验结果,图9(a)为3个矿山尾砂膏体屈服应力随扩散度的分布图. 图9(a)表明尾砂膏体的屈服应力随扩散度呈明显规律性聚集分布,其中3个矿山尾砂膏体的质量分数范围为66%~74%,这代表着目前国内外采用尾砂膏体充填矿山的实际充填质量分数范围. 对尾砂膏体屈服应力与扩散度进行拟合,拟合函数表达式为:

图6 灰砂比为1∶10的不同质量分数尾砂膏体扩散度测试结果. (a)质量分数为68%;(b)质量分数为70%;(c)质量分数为72%Fig.6 Results of spread test of different tailings backfill paste with cement-tailings ratio 1∶10: (a) Cw=68%; (b) Cw=70%; (c) Cw=72%
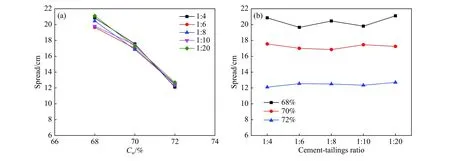
图7 不同配比尾砂膏体扩散度的变化. (a)扩散度随质量分数的变化;(b)扩散度随灰砂比的变化Fig.7 Changes of the spread of tailings backfill paste with different filling ratio: (a) spread changes with mass fraction; (b) spread changes with cementtailings ratio
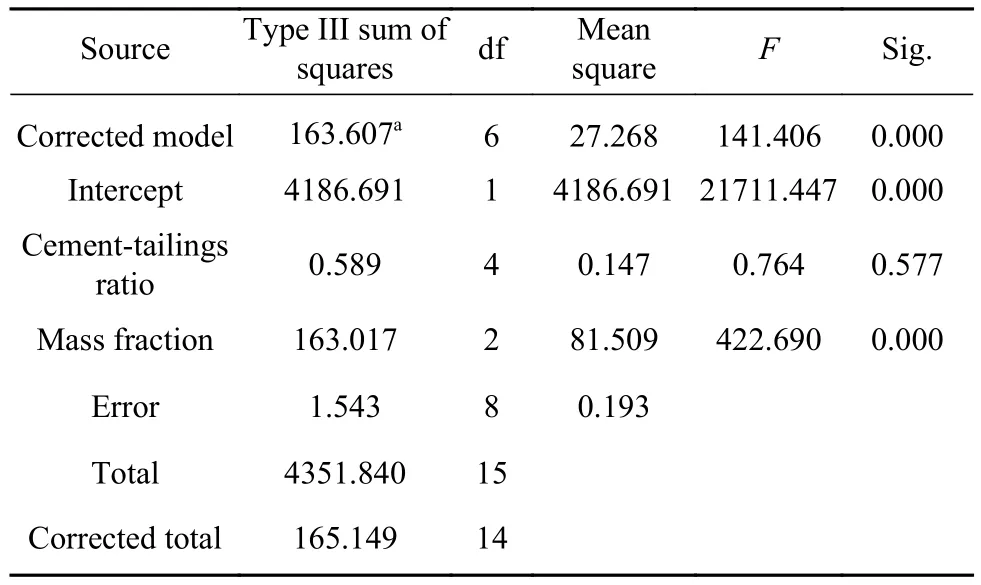
表 3 双因素方差分析结果Table 3 Results of two-way analysis of variance
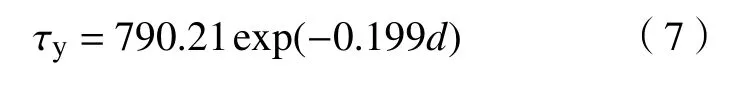
其中,d扩散度,cm. 拟合优度达到0.951,说明屈服应力与扩散度呈指数型函数变化.
图9(b)为3个矿山尾砂膏体黏度系数随扩散度的分布图. 由图9(b)可知,尾砂膏体的黏度系数与扩散度分布较离散,无特定规律,但对于某同一矿山尾砂,其黏度系数与扩散度呈线性分布,黏度系数主要分布在0~0.50 Pa·s范围内.
3.4.2 经验模型验证
为验证屈服应力与扩散度经验模型的准确性,选择青海某铜镍矿和内蒙古某金矿2个矿山尾砂开展验证试验,制备不同配比的尾砂膏体,开展扩散度试验,并利用R/S桨式流变仪测试屈服应力. 将尾砂膏体的扩散度测试结果代入式(7)计算得到其屈服应力,与R/S桨式流变仪测试值作对比,结果如表4所示. 由表4可知,经验模型计算所得屈服应力与R/S桨式流变仪测试结果误差在25%范围内,且尾砂膏体质量分数越高,两者的误差越小,降低至10%范围内.
3.5 经验模型与解析模型对比分析
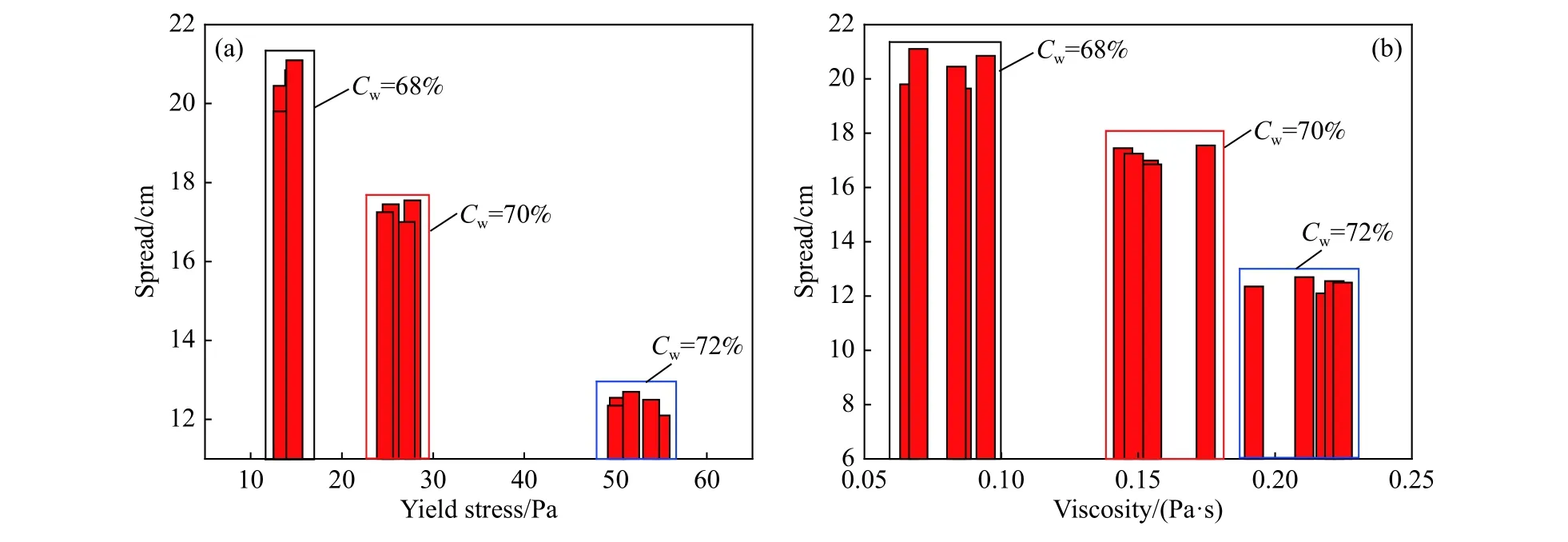
图8 扩散度与流变参数的变化规律. (a)扩散度随屈服应力的变化;(b)扩散度随黏度系数的变化Fig.8 Changes of the spread of tailings backfill paste with rheological parameters: (a) spread changes with yield stress; (b) spread changes with viscosity

图9 不同矿山尾砂膏体流变参数随扩散度的分布图. (a)屈服应力随扩散度的分布;(b)黏度系数随扩散度的分布Fig.9 Distribution of rheological parameters of the different mine tailings backfill pastes: (a) distribution of yield stress and spread; (b) distribution of viscosity and spread

表 4 验证试验结果Table 4 Results of verification test
通过观察上述5个矿山扩散度试验中尾砂膏体的流动形态,均符合解析模型的假定条件,即浆体呈圆饼状向四周均匀流动. 根据扩散度试验结果和式(6)计算得到屈服应力的解析值,其中RH=0.03 m,R0=0.018 m,H=0.06 m,ρ和g分别取1800 kg·m-3和9.8 m·s-2. 解析模型与经验模型的对比如下图10所示. 由图10可知,经验模型与解析模型在扩散度为12~16 cm之间结果较接近,当扩散度由12 cm减小至10 cm或由16 cm增加至30 cm时,两者的差值逐渐增大. 在尾砂膏体屈服应力为0~120 Pa,扩散度为10~30 cm时,解析模型所得屈服应力整体上高于测试值,经验模型计算结果与测试值相差较小.
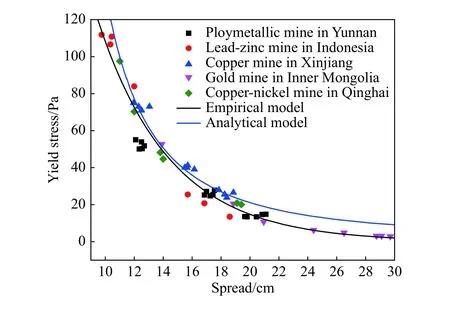
图10 经验模型和解析模型的对比Fig.10 Comparison of analytical model and empirical model
4 工程应用
尾砂膏体通常视为宾汉姆(Bingham)体,在管道输送中的状态像塑性体一样是整体运动,其管道输送阻力方程可由白金汉(Buckingham)方程表示为[21-23]:
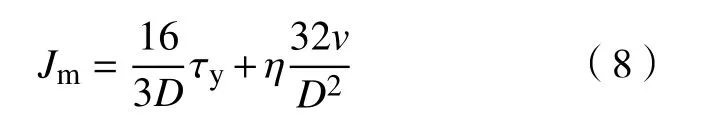
其中,Jm为管流沿程阻力损失,Pa·m-1;η为尾砂膏体黏度系数,Pa·s;D为管道内径,m;v为浆体流速,m·s-1.
若测得尾砂膏体的屈服应力τy和黏度系数η,则可根据式(8)测得管道输送阻力,进而开展管道输送设计. 然而在矿山充填现场,通常无条件直接使用流变仪测试尾砂膏体的流变参数,联立式(7)和(8),可建立管道输送阻力与尾砂膏体扩散度的函数关系,如式(9)所示.
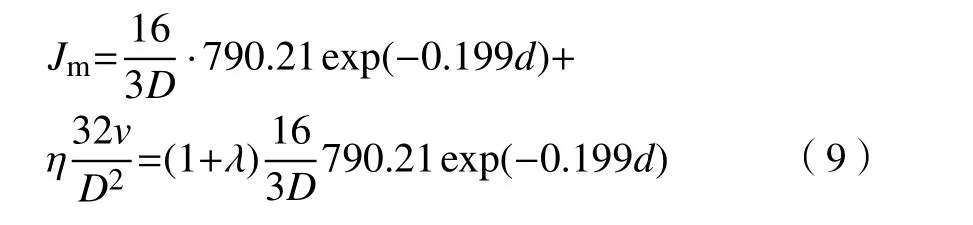
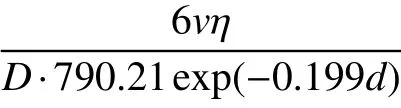
由此,可在矿山充填现场开展扩散度试验,根据扩散度试验结果指导矿山充填管道布置,简单易操作.
5 结论
(1)质量分数是影响尾砂膏体的扩散度的主要因素,灰砂比对扩散度的影响不显著,尾砂膏体的扩散度随质量分数、屈服应力和黏度系数的增加而减小,质量分数为68%、70%和72%的尾砂膏体的扩散度分别为20.37、17.22和12.44 cm,尾砂膏体扩散度的变化规律与其屈服应力及黏度系数的变化趋势相吻合.
(2)尾砂膏体的屈服应力与扩散度呈指数型聚集分布,构建得到屈服应力与扩散度的经验模型,经验模型验证结果表明,屈服应力计算结果与实际测试结果误差在25%范围内,且尾砂膏体质量分数越大,二者的误差越小,达到10%以内,通过测试扩散度可计算得到尾砂膏体的屈服应力.
(3)经验模型与解析模型在扩散度为12~16 cm之间结果较接近. 在尾砂膏体屈服应力为0~120 Pa,扩散度为10~30 cm范围内,解析模型所得屈服应力整体上高于测试值,经验模型计算结果与测试值相差较小.
(4)利用扩散度表征尾砂膏体的流动性,简便易操作,在充填实践中可通过开展扩散度试验,研究尾砂膏体的流变特性,用于指导矿山充填.
