一年级“一图四式”教学难点及突破策略
2020-11-03汤飞梅
□汤飞梅
一、缘起
一年级学生的“一图四式”练习错误率很高。常见错误如下。

第一类错误(左图):出现了7-3=4,这是减法算式中的数字与图中数量不一致。第二类错误(右图):出现了5-3=2,减法算式是图中左边数量减右边数量。学生在面对图式时,知觉系统会自动地将刺激物分为对象和背景,以鸭子图为例,学生能清楚地感知到图中左边和右边的鸭子数量分别是5和3。加法是先反映个别属性,后感知事物整体,因此两个加法算式不成问题。列减法算式时,需先感知整体,后反映部分。当学生整体知觉欠佳时,难以抽象出8只这个背景条件。另一方面,学生对两个加法算式和两个减法算式之间的关系不明晰,加法算式中整体在哪儿?两个部分在哪儿?减法算式整体在哪儿?两个部分在哪儿?学生比较模糊。如何解决“一图四式”中列减法算式有困难的问题?笔者认为,要加强学生的整体感知,加强感知的选择性、理解性和恒常性。
二、实践
(一)分与合中列四式,加强感知的理解性
在感知过程中,理解可以帮助学生把感知对象从背景中分离出来,使感知更稳定。因此,在一图四式列式前,可以先进行如下练习。
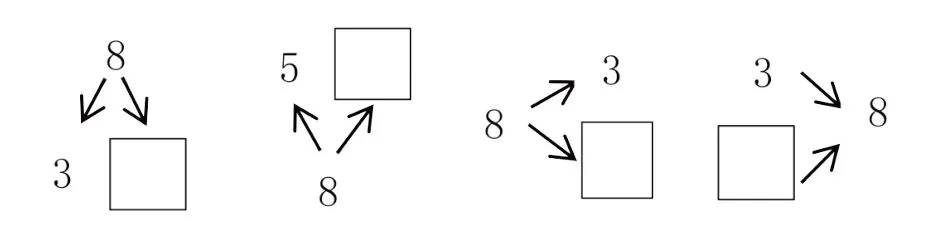
学生根据一组“分成”列两个加法算式、两个减法算式。比如根据8分成3和5,学生可以列3+5=8,5+3=8,8-3=5,8-5=3,四个算式中,8是总数,3与5是部分数。上述四组的表现形式有所不同,总数分别在上面、下面、左边和右边,为后续一图四式的抽象过程做好铺垫。
(二)“多选三”中列四式,加强感知的选择性
学生在感知事物时,对刺激有进行选择性加工的能力,感知系统会自动地将刺激物分为对象和背景。用多个数中选三个数列四个算式进行练习,可以加强感知的选择性。如从3、6、5、10、8中,选择3个数组成两个加法算式和两个减法算式,学生根据数据特点选择5、3、8来列算式,如3+5=8,5+3=8,8-3=5,8-5=3,既积累了数据选择的经验,又培养了数感,同时感受到加法和减法的互逆关系。
(三)图中圈画列四式,加强感知的整体性
在整体感知中,刺激物之间的关系起着重要作用。教学中教师要引导学生把部分与整体圈起来。在圈一圈中,学生既能感知部分是5、3,又能感知整体是8。集合图有三个,求全集就用两个子集“相加”,求子集就用全集“减”其中一个子集。
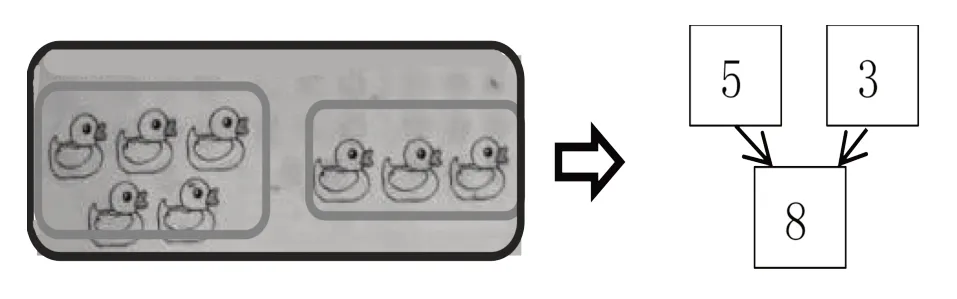
这样列减法算式时,就不会遗漏8。同时,把鸭子数量抽象出来,变成5、3与8,并与“分成”联系起来,列四个算式,学生就不会遗漏8。
(四)变化问题列四式,加强感知的恒常性
感知的恒常性是指客观事物本身不变,但感知条件在一定范围内发生变化时,学生的感知印象仍相对不变。把鸭子图与大括号、问号联系起来,改编成如下一组习题,让学生用三句话来表达每题的两个信息和问题,使部分与整体的关系进一步得到落实,感受到变化的是问题,数量关系没变。

三、思考
这样的尝试较好地解决了学生“一图四式”中列两道减法算式的困难。
(一)多元表征
利用背景和对象的对比变化突出多元表征。圈是低年级学生最常用的手段。在圈一圈中,学生能直观感知对象是左边和右边数量,背景是总数。不同的问题都蕴含数字3、5和8。要引导学生积累“组合”与“分离”的经验。

(二)语言表达
用语言唤起学生头脑中的表象。让学生根据图说意思,如左边5只鸭,右边3只鸭,一共几只鸭?5+3=8只。一共有8只鸭,左边有5只,右边有几只?8-5=3只。在表达中体会信息与信息、信息与问题之间的联系。
(三)题组对比
进行不同问题之间的对比,有助于学生厘清数量关系,形成结构化认识。可把这些错题放在一起讲解对比。
求整体用加法,求部分用减法,要让学生从整体上感受一图四式问题的基本结构和主要特点。有了清晰的结构,遇到大括号和问号的问题,学生就不容易混淆出错。
