怎么做能掌握连续退位减法的算法

□周君斌 潘慧敏

（三年级上册）

计算连续退位减法，如果被减数是整千数，学生特别容易出错。那么，该怎样帮助学生更好地理解和掌握这类减法的算法呢？以“1000-276”为例，可以采用以下教学过程。

一、在独立笔算中感受计算的麻烦

1.教师板书“1000-276”，让学生在练习本上用竖式计算。

2.学生独立计算后，同桌互相说一说竖式计算的方法。在这个过程中，教师找三个计算结果不一样的学生，让他们把计算过程抄写在黑板上。

3.请板书的三个学生说说他们是怎么想、怎么算的。在交流中发现个位上0减6不够减，被减数的十位、百位都是0，要向千位借。当大家对“个位怎样向千位借”有争议时，教师告诉学生可以请计数器来帮忙。

二、在动手操作中探索退位的问题

1.课件出示下面的操作要求，待全班学生完全明确之后，教师再宣布动手操作。

2.反馈时，请一个学生上台演示拨珠操作，其他同学仔细观察。教师要引导学生有理有据地进行操作：①在千位拨上1颗珠；②依据“1个千是10个百”，拨去千位的1颗珠，在百位拨上10颗珠；③依据“1个百是10个十”，从百位拨去1颗珠，在十位拨上10颗珠；④依据“1个十是10个一”，从十位拨去1颗珠，在个位拨上10颗珠。

3.教师利用课件再次清晰、有步骤地展现拨珠的过程。然后请学生闭上眼睛想一想刚才的退位过程和结果。

三、在记录操作中形成抽象的竖式

1.请学生独立思考，尝试在竖式上表示出退位的过程和结果。

2.结合数位顺序图（如下图）的动态演示，通过“学生指挥，教师板书”的方式，师生合作在黑板上形成如右图所示的竖式。

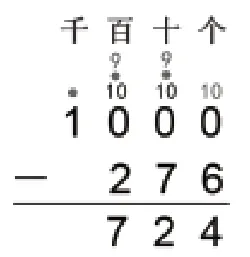
3.同桌交流，相互提问：个位上的10是怎么来的？十位和百位上的数为什么都变成了9？

4.回顾与小结。我们是怎样解决退位的问题的？

听过容易忘记，看过就记住了，做过就理解了。通过在计数器上拨珠，学生不仅亲身经历了连续退位的过程，而且理解和掌握了竖式计算的方法。