CO2中速度5~7 km/s自由飞圆球流场参数的实验测量和数值模拟
2020-11-03廖东骏简和祥谢爱民王宗浩
廖东骏, 柳 森, 黄 洁, 简和祥, 谢爱民, 王宗浩
(中国空气动力研究与发展中心, 四川 绵阳 621000)
0 引 言
火星大气以CO2为主,目前成功着陆的火星探测器进入火星大气的速度主要在5~7 km/s之间[1]。CO2振动特征温度低,高超声速条件下更易发生化学反应,而火星稀薄大气的低密度环境使得气体分子间的碰撞不足以达到热力学平衡和化学平衡状态。因此,探测器在进入火星大气的过程中,CO2条件下的热化学非平衡效应将主导绕探测器的高超声速流动。探测器激波与边界层中非平衡效应是潜在的“宇航任务杀手”之一[2],显著影响探测器进入过程中的气动力系数、气动热载荷和绕探测器流场组分分布等因素,从而影响探测器的控制、热防护和联络通信等性能。因此,需要准确描述探测器在以CO2为主的火星大气环境中高超声速进入时的非平衡流动特性,为探测器的设计提供依据和验证。
数值模拟和地面实验是获得探测器在以CO2为主的火星大气中高超声速进入时非平衡气动特性的2种主要手段。在数值模拟方面,目前主要基于Park的双温度非平衡模型[3]和Park′94化学反应动力模型[4]对CO2中的非平衡绕流进行数值模拟。相关研究表明,当CO2中来流速度低于8 km/s时,采用简化的Park′94 5组分(CO2, CO, O2, O, C)或8组分(N2, O2, NO, O, N, C, CO, CO2)和双温度非平衡模型就可以较好地描述火星大气主要成分CO2或CO2-N2混合气体中的非平衡流动[5-7]。本文也拟基于上述热化学模型对实验流场进行模拟,通过对比实验数据验证模型准确性,并分析流场参数。
在地面实验方面,主要采用激波风洞和膨胀管等高焓脉冲设备研究CO2条件下的非平衡流动,测量的数据包括激波脱体距离、气动力系数、热通量和辐射光谱等多种流场参数[8-11]。但部分高焓脉冲设备来流的热化学状态可能存在不确定性[12]。MacLean等[13]在LENS I激波风洞和LENS XX膨胀管风洞上进行的CO2中火星探测器缩比模型非平衡绕流测量对比实验表明,反射式激波风洞的来流存在已离解气体。Matthew等[14]研究评估了T5和LENS I激波风洞在火星探测器非平衡流场测量实验方面的能力,发现驱动气体对实验气体的污染也是导致来流状态不确定的原因之一。诸如上述的问题导致部分高焓脉冲设备实验测量结果与其他设备存在差异,并给数值模拟验证带来困难。弹道靶自由飞实验可同时模拟真实的气体介质、雷诺数和马赫数,可复现真实的飞行环境[15]。已有部分研究在弹道靶上测量了CO2中飞行速度5 km/s以下的探测器缩比模型气动力、动稳定性、圆球和探测器缩比模型的激波脱体距离等[16-19]。然而,弹道靶自由飞实验的模型尺寸较小、测试手段有限、测量难度大,需要精确的测量方法以获得可靠的实验数据。激波脱体距离是弹道靶实验中直观且易于测量的实验数据,圆球模型是研究激波脱体距离的标准模型之一,无法正确预测圆球激波脱体距离意味着无法正确预测飞行器的激波形状和压力分布,从而影响飞行物体总体气动特性的预测[20]。圆球激波脱体距离一般随来流速度升高而呈现逐渐减小的趋势,在一定程度上反映了流动中化学反应的剧烈程度,但目前较缺乏在弹道靶中获得的CO2条件下飞行速度5 km/s以上的圆球激波脱体距离实验测量数据,需要开展测量实验补充相关数据。
本文针对火星探测器进入速度范围5~7 km/s的状态,在中国空气动力研究与发展中心超高速空气动力研究所(HAI,CARDC)超高速弹道靶上测量CO2条件下自由飞圆球的激波脱体距离。研究CO2条件下约5~7 km/s速度范围内激波脱体距离随来流速度的变化关系,将测量得到的激波脱体距离实验数据与采用双温度非平衡模型和简化的Park′94 5组分6反应模型数值计算的结果进行对比验证,并采用数值方法计算圆球绕流的温度和组分分布等流场参数,以进一步分析本文实验状态下自由飞圆球的热化学非平衡绕流特性。
1 超高速弹道靶自由飞实验
1.1 实验设备
自由飞圆球激波脱体距离的测量实验在中国空气动力研究与发展中心超高速空气动力研究所的超高速弹道靶上进行,实验设备和测试系统的布置如图1所示。实验的靶室包括爆震段和实验段,由真空系统置换靶室内实验气体并提供预定的靶室压力。口径16 mm的二级轻气炮将圆球加速到预定速度并在靶室内自由飞行。采用脉宽10 ns的YAD激光器作为光源对圆球绕流流场进行阴影成像,阴影光路的布置和测试方法可参考文献[21]。靶室的压力和温度由电子真空计和温度计测量。

图1 实验设备和测试系统示意图
1.2 圆球模型与实验状态
圆球模型直径D=6 mm,材质为氧化铝,质量为0.45 g。氧化铝圆球为陶瓷材料烧结制成,其直径误差<0.01 mm。模型飞行速度V选取为针对火星探测器进入速度的范围约5~7 km/s,靶室压力p0选取为约11 kPa,靶室温度T0为室温。图2给出了圆球模型的照片。

图2 实验模型
1.3 实验结果
实验在纯CO2条件下进行,基于拍摄到的圆球绕流流场阴影照片测量激波脱体距离,测量方法和误差分析可见文献[18],用测量的激波脱体距离δ除以圆球半径R,就能得到无量纲的激波脱体距离δ/R。共获得6个有效的自由飞圆球激波脱体距离实验测量数据,其实际飞行速度为4.562~7.314 km/s(Ma=17.3~27.6)。表1给出了具体的实验测量数据和对应实验状态,这也是国内首次获得的CO2条件下飞行速度5 km/s以上的自由飞圆球激波脱体距离实验数据。图3和4分别给出了实验0021(V=5.715 km/s,p0=11.01 kPa,ρR=6.17×10-4kg/m2)和实验0025(V=7.314 km/s,p0=11.08 kPa,ρR=6.17×10-4kg/m2)拍摄到的圆球绕流流场阴影图像,图中可以明显地分辨出脱体激波。图5给出了本实验测量的激波脱体距离随飞行速度的变化趋势,并将其与一组先前在CO2条件下测量得到的飞行速度在5 km/s以下的半径5 mm圆球激波脱体距离实验测量数据[19]进行了对比。即使在考虑测量误差和实验环境压力差异影响的前提下,当圆球飞行速度在5 km/s以下时,圆球激波脱体距离基本随飞行速度升高呈现单调减小趋势。而当圆球飞行速度由约5.5 km/s升高到约7.0 km/s的过程中,圆球激波脱体距离随飞行速度升高呈先减小后增大的趋势,与通常认为的激波脱体距离随来流速度升高而单调减小的趋势不一致。该现象推测与该速度范围内圆球绕流流场的热化学状态变化有关,后文将结合数值模拟对其进行分析。

图3 实验0021阴影图像

图4 实验0025阴影图像

图5 激波脱体距离实验测量数据随飞行速度变化

表1 激波脱体距离实验测量数据和对应实验状态Table 1 Measured shock standoff distances and corresponding test conditions of present test
2 数值模拟
2.1 数值方法
采用带化学反应源项的二维轴对称N-S方程组作为控制方程,在坐标系(x,r,θ)下,其无量纲形式表达为:
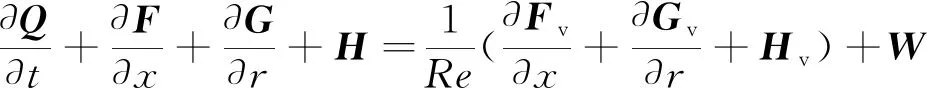
(1)
式中,Q为守恒量矢量,F、G为对流项矢量,Fv、Gv为黏性项矢量,H、Hv为有黏、无黏部分源项矢量,W为化学反应和振动源项矢量,Re为雷诺数。对双温度非平衡模型,有:
Q=(ρi,ρu,ρv,ρE,ρevib)T
(2)

(3)

化学反应模型采用简化自Park′94模型[4]的5组分(CO2,CO,O2,O,C)6反应模型,其反应方程式为:
CO2+m1←→CO+O+m1
CO+m2←→C+O+m2
O2+m3←→2O+m3
CO+O←→O2+C
CO2+O←→O2+CO
CO+CO←→CO2+C
其中m1、m2和m3为第三体组分,各反应的反应常数和三体碰撞效率选自文献[4]。各组分的施密特数Sc取为常值0.525。
热力学温度模型采用Park的双温度非平衡模型[3]。对本文涉及的2种化学反应,其反应控制温度分别取为:离解反应(AB+M↔A+B+M),正、反应控制温度Tf、Tb为:Tf=(TTvib)0.5(即振动温度指数q=0.5),Tb=T;置换反应(AB+C↔A+BC),其正、反应控制温度Tf、Tb为:Tf=Tb=T。其中T和Tvib分别为平(转)动温度和振动温度。
二维轴对称结构网格如图6所示,网格数量为12 000,并在激波位置处加密。控制方程对流项采用对称型TVD格式离散,黏性项采用中心差分格式离散,化学反应和振动源项采用一阶精度的隐式处理。壁面边界为无滑移等温壁,壁面温度Tw取为1000 K;壁面组分计算采用完全催化壁条件,壁面组分质量分数取等于来流组分质量分数,对本文实验状态,来流CO2组分质量分数取为1。

图6 计算网格示意图
2.2 计算结果及对比分析
2.2.1 激波脱体距离
图7对比了自由飞圆球激波脱体距离的实验测量数据和数值计算结果。其中红色虚线和灰色点划线分别是实验前在压力p0=11.5 kPa、T0=300 K状态下采用双温度模型和冻结气体模型计算的圆球激波脱体距离随速度变化趋势。蓝色空心方框为根据本文具体实验状态采用双温度模型计算的对应圆球激波脱体距离。上述计算涉及的化学反应动力模型均为本文选取的5组分6反应模型。冻结气体模型计算的激波脱体距离随速度升高而呈单调减小趋势。双温度模型计算的两组结果则表现出相似的变化规律:当圆球飞行速度在约5.5 km/s以下时,激波脱体距离随速度升高而减小;当飞行速度在约5.5~7.0 km/s时,激波脱体距离随速度升高反而增大;当飞行速度超过7.0 km/s时,激波脱体距离又随速度升高而呈缓慢下降趋势。该变化规律与实验测量的激波脱体距离随速度变化趋势基本一致。表2对比了根据本文实验状态采用双温度模型和5组分6反应模型计算的激波脱体距离与对应实验测量数据的偏差,可见采用本文计算方法得到的圆球激波脱体距离基本再现了本文实验测量数据。
此外,还针对不同圆球直径、不同双尺度参数和不同振动温度指数q等条件计算了本文实验状态下的激波脱体距离。得到的计算结果均表现出激波脱体距离在来流速度约5.5~7.0 km/s时随来流速度升高反而增大的趋势。只有在假设流动的化学反应冻结时,数值计算才能得到激波脱体距离随来流速度升高而始终单调减小的结果。由此推测,本文实验测量数据所体现出的自由飞圆球激波脱体距离随飞行速度变化的趋势应与其绕流热化学状态有关,需进一步计算其流场温度和组分分布进行分析。

图7 自由飞圆球激波脱体距离的实验测量数据和数值计算结果对比

表2 双温度模型和5组分6反应模型计算的激波脱体距离与实验数据的偏差
2.2.2 流场温度分布
选取本文飞行速度不同的3个实验,分别为:实验0021(V=5.715 km/s)、实验0024(V=4.562 km/s)和实验0025(V=7.314 km/s),并根据其实验状态计算其流场温度分布。图8(a)、(b)分别对比了根据具体实验状态计算得到的实验0021和实验0024、实验0021和实验0025的驻点线平动、振动温度分布。在激波后靠近激波一侧,上述算例的平动温度T对比振动温度Tvib均有显著差别,表现出显著的热力学非平衡现象。但对比上述各算例的温度变化趋势,尽管其温度分布位置由于脱体激波位置不同而有所差异,但其总体分布趋势是类似的,松弛距离也基本相同。由此推测,热力学非平衡并非是引起来流速度约5.5~7.0 km/s时激波脱体距离随速度升高反而增大的原因。


图8 驻点线平动温度T和振动温度Tvib分布数值计算结果对比
2.2.3 流场组分分布
进一步计算上述3个算例的流场组分摩尔质量分数分布。图9(a)、(b)分别对比了根据具体实验状态计算得到的实验0021和实验0024、实验0021和实验0025的驻点线各组分摩尔质量分数分布。上述算例激波后靠近激波一侧的流场组分含量有显著变化,表明激波层中产生了剧烈的化学反应。结合图8的计算结果,可推测本实验状态下自由飞圆球波后靠近激波一侧区域的流场主要处于热化学非平衡状态。对比实验0021和实验0024的计算结果,当圆球飞行速度由4.562 km/s提高到5.715 km/s时,组分CO2和O2的含量显著降低,组分CO和O的含量明显升高,而组分C的含量没有发生变化,基本为0。该结果表明,当来流速度由约4.5 km/s升高到约5.5 km/s时,激波后CO2迅速离解成CO和O,并与O发生置换反应生成O2,生成的O2也迅速离解,而CO的离解和置换反应尚未发生,没有C生成,仍处于化学冻结状态。对比实验0021和实验0025的计算结果,当圆球飞行速度由5.715 km/s提高到7.314 km/s时,组分CO含量有所降低,组分CO2和O2含量显著降低,基本接近于0,组分O的含量有所升高,而组分C的含量也明显升高了。该结果表明,当来流速度由约5.5 km/s升高到约7.0 km/s时,CO2和O2离解反应的程度进一步加大,已基本完全离解,而CO也已开始离解,在波后靠近激波一侧处于化学非平衡状态,与来流速度5.5 km/s以下CO处于化学冻结的状态不同。CO离解后生成C和O,物质的量增加了,波后气体体积(物质的量×气体摩尔体积,其中后者为常量)相对增大,而气体总质量不变,因此波后气体密度相对降低。根据Lobb[22]提出的激波脱体距离δ的理论关系式:


图9 驻点线组分摩尔质量分数分布数值计算结果对比

(4)
式中,L为常数,对圆球其取值为0.41,D为圆球直径。对来流密度ρ∞基本一致的本文实验状态,当波后密度ρs降低时,激波脱体距离将升高。图10对比了根据实验0021和0025状态计算的驻点线密度分布,可见当来流速度由约5.5 km/s(0021)升高到约7.0 km/s(0025)时波后密度确有降低。故根据上述计算结果推测,当来流速度在约5.5~7.0 km/s的范围内时,组分CO开始发生显著离解,使得其波后密度随速度升高而降低,导致激波脱体距离反而随速度升高而增大。
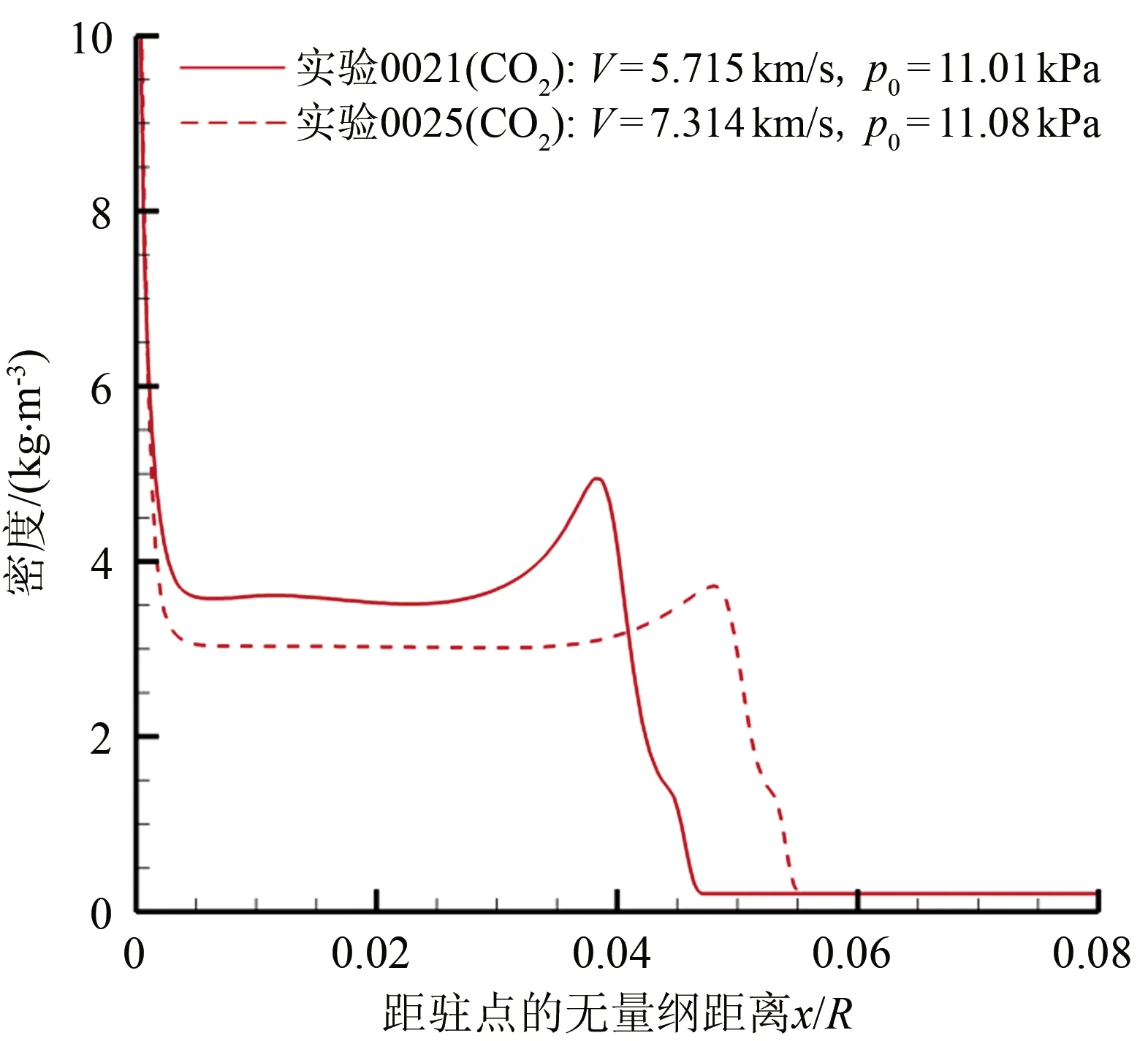
图10 实验0021和实验0025状态下驻点线密度分布数值计算结果对比
3 结 论
本文在中国空气动力研究与发展中心超高速空气动力研究所弹道靶上测量了CO2中针对火星探测器进入速度范围5~7 km/s条件下的自由飞圆球激波脱体距离,并通过与数值计算得到的流场参数对比,得到以下结论:
(1) 在本文实验状态下,圆球飞行速度约5.5~7.0 km/s范围内,圆球激波脱体距离反而随飞行速度升高而增大;
(2) 采用Park的双温度非平衡模型和5组分6反应CO2化学反应动力模型可基本再现本文自由飞圆球激波脱体距离实验测量数据,且根据计算结果推测,本文实验状态下自由飞圆球波后靠近激波一侧区域的流场主要处于热化学非平衡状态;
(3) 根据计算结果推测,当来流速度在约5.5~7.0 km/s的范围内时,流场组分CO开始发生显著离解,这是引起圆球激波脱体距离在该速度范围内随速度升高反而增大的可能原因。
