扰动激波冲击界面不稳定性：反射激波效应

权 通, 廖深飞, 邹立勇,*, 邱 华

(1.西北工业大学 动力与能源学院, 西安 710072; 2.中国工程物理研究院流体物理研究所 冲击波物理与爆轰物理重点实验室, 四川 绵阳 621900)

0 引 言

当激波冲击两种不同密度流体的界面时，界面上的扰动会随时间增长，最终出现湍流混合结构，这种现象称为Richtmyer-Meshkov(RM)不稳定性[1-2]。RM不稳定性在天体物理[3]、惯性约束聚变(Inertial Confinement Fusion，ICF)[4-5]、水中爆炸[6]以及常规兵器[7]等研究领域中有着广泛的应用背景，其界面演化机制包括由激波折射、反射、衍射、聚焦、发散等引起的压力扰动，以及由压力梯度和界面密度梯度不共线引起的斜压涡量沉积。

半个多世纪以来，国内外专家和学者从理论分析、实验研究和数值模拟3个方面针对RM不稳定性问题开展了大量的研究，并取得了丰硕的学术成果[8-11]。在实际工程应用中，界面往往受到激波的多次加载，因此，研究反射激波作用下的RM不稳定性显得尤为重要。1976年Andronov等[12]首次研究了反射激波作用下的RM不稳定性问题，在随后的几十年里，研究者们陆续针对这一问题，开展了系列研究，涉及到单模[13]、多模[14]、气泡[15]、气帘[16]和气柱[17-19]等多种界面情形。这些工作表明，反射激波的二次冲击作用会显著加快界面扰动的增长。

需要说明的是，以上研究只考虑了入射激波是均匀激波的情形。无论如何，在实际工程应用中，激波作用于界面之前往往是扰动激波，如在ICF中，在非均匀激光照射下，靶丸内爆产生的冲击波必然是非均匀的，同时靶丸表面粗糙度也会对冲击波造成干扰[4-5]。在扰动激波的冲击下，界面也会失稳变形，而目前国内外学术界关于这类问题的研究较少。Ishizaki等[20]通过数值模拟发现，在正弦形激波的诱导下，界面演化规律与经典RM失稳现象存在很大差异，界面扰动增长率依赖于激波到达界面时的相位。刘金宏等[21]利用竖式激波管对绕柱激波作用下的RM不稳定性问题进行了实验研究,并分析了激波强度对界面演化的影响。针对不同的入射波形，Zou等[22]对绕柱激波诱导的界面演化过程进行了实验及分析，指出压力扰动机制在界面演化过程中起主导作用，经过与经典的Richtmyer理论解对比发现，绕柱激波诱导的界面演化增长率明显小于传统基于经典RM理论预估得到的扰动增长率。Liao等[23]进一步研究了绕柱激波作用下的界面发展的Atwood数(定义为A=(ρ2-ρ1)/(ρ2+ρ1)，ρ1和ρ2分别为界面两侧流体的密度)效应，表明扰动振幅增长率随Atwood数的增加而减小。另外，Zhai等[24]还研究了多圆柱情形下绕柱激波冲击界面的RM不稳定性问题。最近，Zou等[25]数值模拟研究了绕柱汇聚激波冲击下的界面不稳定性，定量分析了脉冲速度振荡、连续压力振荡及几何汇聚效应对界面演化的影响，提出了一种改进的脉冲模型来预测扰动激波冲击下界面扰动的增长。

本文在前期绕柱激波入射阶段冲击界面演化工作[22]的基础上，通过高速纹影技术和Mie散射技术，进一步获得了反射激波作用下N2/SF6界面演化图像，对反射激波二次冲击后的界面演化过程进行研究，并将实验结果与理论模型结果进行了对比分析。

1 实验方法

1.1 实验装置及初始条件

实验在图1所示的竖式激波管中开展，激波管由驱动段(1.60 m)、被驱动段(4.22 m)和实验段(0.31 m)组成，内腔截面尺寸为100 mm × 100 mm。驱动段填充高压N2，被驱动段填充常压N2，二者之间用聚乙烯薄膜隔开，采用电加热电阻丝破膜方式产生平面入射激波。在激波管侧壁安装了3个压力传感器，用于测量初始平面入射激波速度和触发高速摄影系统。将直径为d的刚体圆柱安装在界面上方、其圆心到界面距离为l的位置，平面入射激波自上而下传播时，遇到刚体圆柱发生绕射，形成入射扰动激波。采用与Jacobs等[26]类似的方法，在实验段底部和低压段顶部分别同时缓慢充入SF6和N2，2种气体在观测段顶部相遇后，从两侧狭缝中溢出，形成无膜初始均匀界面。在我们前期入射阶段实验工作[22]中，为研究直径d和距离l对扰动激波冲击界面时刻的波形及随后界面演化过程的影响，定义了无量纲距离η=l/d，并开展了3种不同η情形的实验，具体参数见表1，所有情形下入射激波马赫数均满足Ma= 1.22±0.01。本文关注的是入射扰动激波冲击界面后，其透射激波在实验段底部端壁处反射，从而二次冲击入射阶段形成的N2/ SF6界面。因此，用无量纲距离η表征反射激波二次冲击前界面的初始形状。

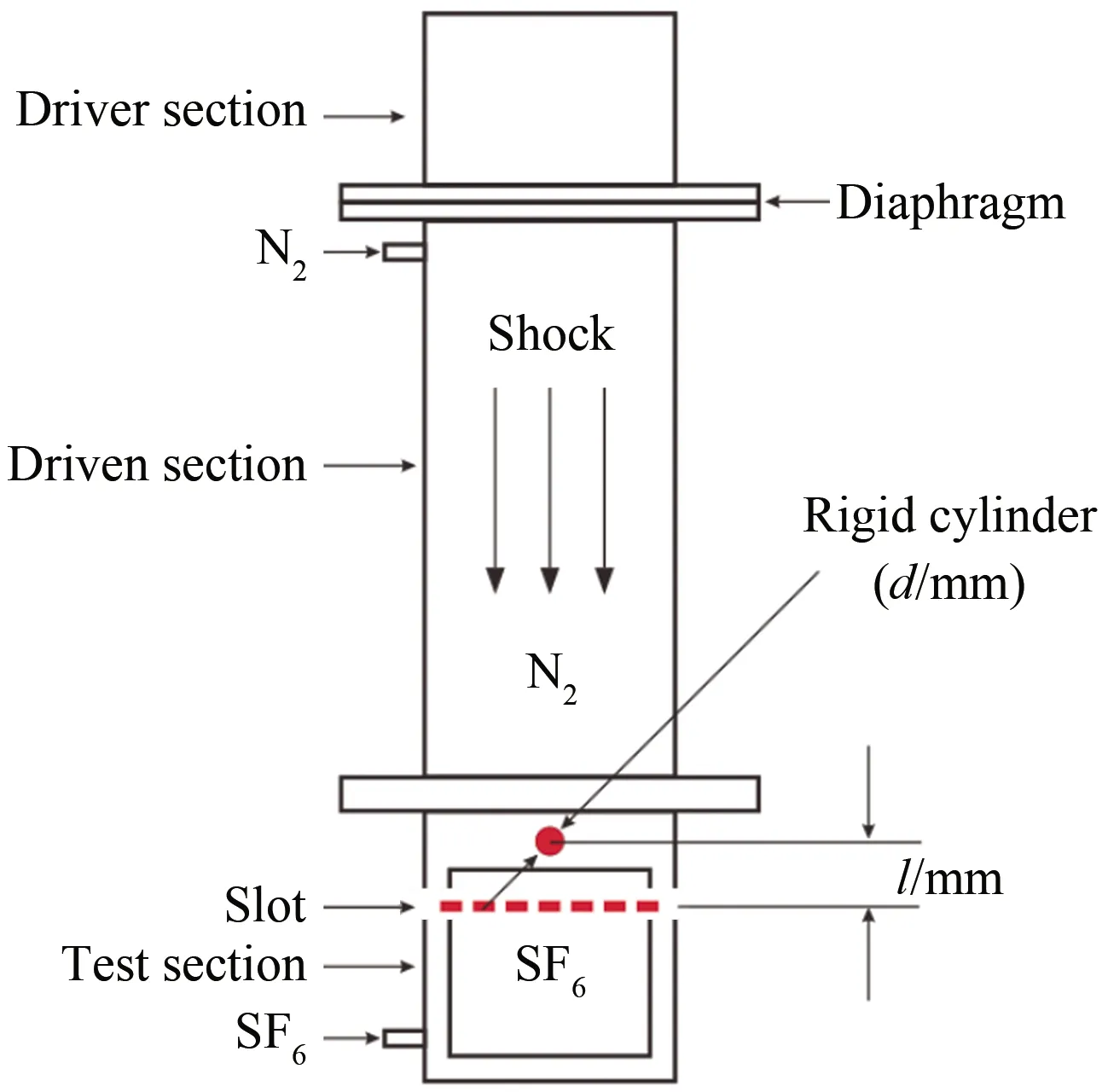
图1 竖式激波管示意图

表1 3种情形的实验参数Table 1 Experimental parameters for three cases

1.2 测试方法

图2给出了实验采用的2种测试方法。图2(a)为高速纹影系统示意图，由氙灯光源(功率500 W)、狭缝、凹面镜(直径300 mm，焦距3 m)、刀口和高速摄像机(Photron FASTCAM，幅频取为6300帧/s)等组成。图2(b)为平面Mie散射系统示意图，重气体SF6从高压气瓶充入测试段上方的气箱中，通过转式测速仪和小型截止阀来控制流速。当气箱中SF6体积达到98%以上(通过SF6气体分析仪FT-103P监测)时，为便于观测，将烟雾发生器产生的白色乙二醇烟雾充入SF6气箱中。为了让SF6和乙二醇烟雾良好混合，烟雾喷嘴设计在气体箱的底部侧壁位置。需要说明的是，乙二醇烟雾与重气体体积比大约为1∶105，这意味着添加乙二醇烟雾对重气体的密度影响很小(低于0.1%)。实验中乙二醇烟雾颗粒直径约为0.5 μm，其对SF6气体的良好跟随性已在Zou等[27]及Rightley等[28]的类似实验中得到验证)。实验时激光器发出的柱形激光(频率10 kHz，波长532 nm，脉宽10 ns)通过一组透镜和反射镜后，转化为厚度约1 mm的片光源，透过实验段底部玻璃窗照射流场，采用高速摄像机(Photron FASTCAM，幅频取为10 000帧/s)对界面演化过程进行拍摄，进而获得流场中界面演化结构图像。

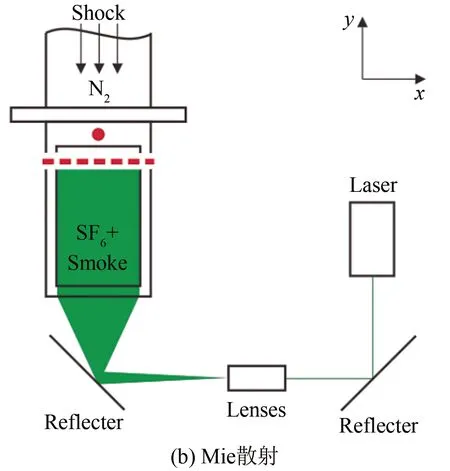
图2 两种测试技术示意图

2 实验结果与讨论

2.1 反射激波作用下界面演化形态

图3给出了η=4.0情形下入射激波和反射激波冲击N2/SF6界面演化纹影像，关于入射阶段的界面演化规律，我们前期已有分析[22]，所以这里主要讨论反射阶段。令t=0 ms为反射激波刚好到达界面的时刻，由图可知，入射扰动激波由于在运动过程中的不断整形和致稳趋势，t=-0.12 ms时刻从激波管下端壁向上运动的反射激波的振幅已衰减至几乎为零，因而可以近似当作平面激波来处理。 反射激波到达之前，界面演化为“Λ”形结构，两侧呈向下凹陷，中心有1个N2气腔。因此，反射激波作用后的界面演化过程可近似处理为平面激波诱导的经典RM不稳定性问题。反射激波从重流体SF6进入轻流体N2后，界面发生了相位反转，随后整体的“Λ”形界面演化成气泡，中间的气腔处形成尖钉。随着时间的推移，尖钉和气泡逐渐增长。t=1.47 ms时，界面下方可以看到一道来自下端壁的反射稀疏波，这道稀疏波将对界面演化产生影响。本文只考虑反射激波作用下的界面不稳定性问题，因此只对反射稀疏波到达界面前的实验结果进行分析。

图3 高速纹影技术获得的入射阶段和反射阶段N2/SF6界面演化图像 (η =4.0)

由于纹影观测技术沿光路方向有积分效应，为了获得更精细的实验图像，进一步采用平面Mie散射技术得到反射激波二次冲击N2/SF6界面演化图像(见图4)。可以看到，η=4.0情形下，反射激波作用之前，界面总体呈现为“Λ”形，中间上部为开口的N2气腔(实线圆圈区域)，两侧各有一个界面台阶(虚线圆圈区域)，这与图3观察到的结果是一致的。随着η的减小，气腔位置越来越深，面积逐渐减小，上部逐渐闭合。当η=2.0时，气腔几乎完全消失。反射激波冲击界面后，从图4中可以观察到与图3类似的相位反转以及随后的气泡和尖钉发展过程。当η=2.0时，界面演化总体上呈现为一个气泡结构，而当η=3.3和4.0时，在气泡之外，还出现了界面中心位置的尖钉结构；当η=3.3时，界面中心的尖钉结构相当明显，距离气泡结构很近，位于气泡上沿的下方；当η=4.0时，界面中心的尖钉则较为纤细，距离气泡结构较远，位于气泡上沿的上方。这是由不同η情形下反射激波冲击前的界面形状及位置差异造成的。

图4 Mie散射获得的反射激波作用下N2/SF6界面演化图像。实线圈区域为气腔，虚线圆圈区域为台阶，a为混合区宽度

图5以η= 4.0情形为例，对图4中气泡和尖钉结构的形成原因进行说明。反射激波由下向上传播的过程中，由于界面密度梯度与激波压力梯度不共线，引起斜压涡量沉积，“Λ”形界面左侧和气腔右侧的斜压涡量为负(顺时针方向)，“Λ”形界面右侧和气腔左侧的斜压涡量为正(逆时针方向)。在斜压涡作用下，总体上“Λ”形界面结构向下翻转形成气泡，而界面中心气腔则向上翻转形成中心尖钉。随着η的逐渐减小，中心气腔面积更小、位置更深，因而反射激波冲击后，中心尖钉高度逐渐变小，η= 2.0情形下，中心尖钉完全消失。

图5 反射激波作用下界面斜压涡量沉积示意图

2.2 实验结果和理论模型的定量对比

如图6(a)图像所示，反射激波作用前界面图像形状与标准“Λ”形较为接近。为便于与理论模型进行比较，这里将图6(a)中的界面近似处理为标准“Λ”形界面。首先，提取界面轮廓曲线上的坐标点，如图6(b)中圆点所示；然后，采用分段双线性方法进行拟合，得到如图6(b)黑色实线所示的标准“Λ”形界面。定义初始振幅a0为标准“Λ”形界面顶点与底部端点连线的垂直距离，初始波长λ0为标准“Λ”形界面底部两端点间距W0的2倍，波数k=2π/λ0，初始夹角θ0为标准“Λ”形界面的顶角。a0、λ0和θ0之间的关系为：

图6 反射激波到达前的扰动界面形状

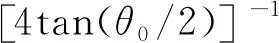
(1)

表2给出了3种情形下的a0、λ0、θ0和a0/λ0等界面参数，界面初始振幅和初始波长的比值a0/λ0随η的增加而减小。当η=2.0和3.3时，a0/λ0均大于0.1，不满足线性初始条件，而当η=4.0时，a0/λ0小于0.1，满足线性初始条件。

表2 “Λ”形界面参数Table 2 Parameters of “Λ” shaped interface

Mikaelian[29]通过傅里叶分析法发现，“Λ”形界面可以表示为系列正弦界面相加的形式：

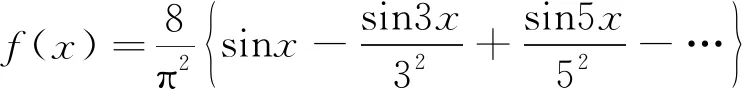
(2)

取一阶近似可得到:

(3)

也就是说，“Λ”形界面和与其振幅、波长相等的正弦单模界面具有81.8%(8/π2)的相似度。因此，后续可采用基于正弦界面的理论模型来比较分析反射阶段混合区宽度的演化规律。

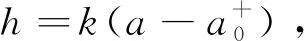
图7中点状图为无量纲处理后的实验混合区宽度随时间变化曲线。在初始冲击压缩阶段，混合区宽度逐渐减小，反射激波离开界面后，伴随着相位反转过程的发生，混合区宽度进一步减小。此后，混合区宽度开始逐渐增加，演化早期混合区宽度是线性增长的，随着时间的发展，界面扰动振幅越来越大，混合区宽度开始呈非线性增长趋势。还可以看到，在η= 2.0和3.3时，混合区宽度线性增长的持续时间较短，而η= 4.0时混合区宽度线性增长的持续时间较长，这是因为只有该情形下界面的初始振幅与波长之比a0/λ0小于0.1，满足线性初始条件。

图7 混合区宽度随时间变化曲线：实验和MB模型对比

针对激波冲击重/轻界面情形，在相位反转发生后的混合区早期发展过程，Meyer和Blewett[30]修正了经典的Richtmyer模型[1]，提出初始振幅取波前和波后振幅的平均值，由此给出了振幅线性增长率的修正公式(MB模型)：

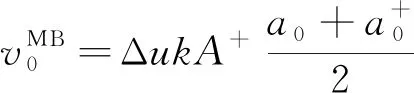
(4)

表3 理论模型增长率 Table 3 Growth rate calculated by theoretical model

随着界面的演化发展，线性模型不再适用，混合区宽度开始非线性增长，对此Dimonte和Ramaprabhu[31]提出了一种弱非线性理论模型(DR模型)，用来计算线性阶段和非线性段早期尖钉和气泡前沿的增长率。该模型公式为：

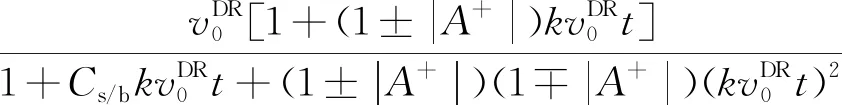
(5)

(6)

其中，vs和vb分别为尖钉和气泡前沿增长率，Cs和Cb为无量纲参数，由初始波数、初始振幅和波后界面Atwood数确定。对式(5)积分，可得到尖钉和气泡前沿的位移as和ab，进而得到界面混合区宽度a=(as+ab)/2。

对于大振幅情况下的界面演化增长率，Dimonte和Ramaprabhu[31]提出作如下修正：

(7)

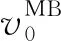
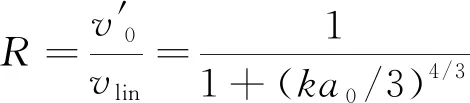
(8)

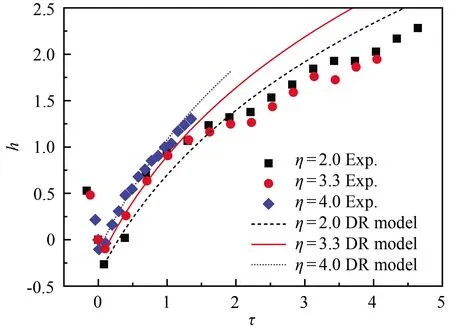
图8 混合区宽度随时间变化曲线：实验和DR模型对比

3 结 论

利用竖式激波管装置开展了绕柱扰动激波冲击N2/SF6界面不稳定实验，分析研究了反射激波作用下的界面演化过程，得到以下结论：

(1) 反射激波到来前，界面已演化成“Λ”形结构，包含两侧的台阶和中心的气腔。在反射激波的冲击作用下，“Λ”形界面整体上演化为气泡结构，在η=3.3和4.0情形，界面中心气腔还演化出尖钉结构，而在η=2.0情形，由于中心气腔太小，没有尖钉结构出现。

(2) 界面演化先后经历了压缩阶段、反相阶段、线性增长阶段和非线性增长阶段。MB模型能够预测线性段混合区宽度的增长趋势，而DR模型则可以合理地预测线性阶段和非线性阶段混合区宽度的增长规律。相比较而言，在η=4.0情形下，DR模型的预测效果最好，而在η=3.3情形下，由于气泡混合区宽度发展受到中心尖钉结构的影响，预测效果最差。

致谢:感谢国家自然科学基金(11672277，11602247，51676164，91952205)对本文研究工作的支持。感谢刘金宏在实验过程中提供的技术支持。