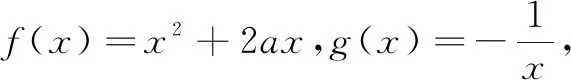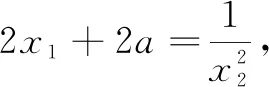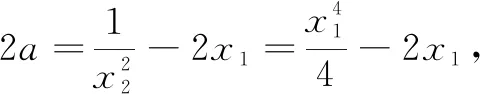运用“一点三方程”求解曲线的切线问题
2020-11-01吴志峰
吴志峰
(福建省厦门外国语学校石狮分校,362700)
一、问题的提出
最近,笔者在教学过程中遇到如下数学问题.
引例已知直线y=ax+b(b>0)与曲线y=x3有且只有两个公共点A(x1,y1),B(x2,y2),其中x1 (A)-1 (B)0 (C)1 (D)a 所以2x1+x2=0,选B. 反思本题学生的解答不够理想,要么是题意理解不够深刻,没有看出是切线问题;要么是面对含参数的切线问题解题思路不明,无法制定明确、有效的解题方案.事实上,对于涉及直线与曲线相切的问题,笔者认为处理的关键是抓住“一点三方程”,即抓住切点及以下三个方程:切点在曲线上,切点坐标满足曲线方程;切点在切线上,切点坐标满足切线方程;曲线在切点处的导数等于切线方程的斜率.本文从以下几方面介绍一点三方程法解决涉及曲线切线的有关问题,通过明确示范,进一步提高学生的数学运算素养. 直线与二次曲线相切,通常只需将直线与二次曲线方程联立,通过一元二次方程有唯一解,由判别式为零来获得切点等信息,从而求出切线方程. 由对数均值不等式知上式显然成立. 综上,x1x2>e2成立. 评注在解含有参数的极值点偏移问题时,常常利用题目已给的式子进行加、减两类运算,然后构造出(指数)对数均值不等式进行证明. 例5已知函数f(x)=x-aex(a为常数)有两个不同的零点x1,x2,请证明:x1+x2>2. 证明借助a作为媒介,构造指数均值不等式. 由指数均值不等式(结论2)知上式显然成立,因此x1+x2>2成立. 例1直线y=x+m与抛物线y=x2相切,则切线方程为______. 对于非二次曲线的切线问题,联立方程组所得一元方程往往不是一元二次方程,此时判别式法就不再适用了,相应问题一般可利用导数的几何意义来进行处理. 1. 已知切点或切线方程的情形 例2求曲线f(x)=x3+2x-1在x=1处的切线方程. 解依题意,由f(1)=2,可知切点为A(1,2).又f′(x)=3x2+2,由导数的几何意义,可知切线斜率为k=f′(1)=5.于是,所求切线方程为y-2=5(x-1),即y=5x-3. 评注若将本题中的切线方程y=5x-3与曲线方程y=x3+2x-1联立,整理可得x3-3x+2=0,即(x-1)2(x+2)=0,解得x=-2或x=1.由此可见,直线与曲线相切时不一定只有一个交点.因此,对于非二次曲线无法用判别式法来求切点. 2.切点或切线方程皆未知的情形 如同引例,此类情形问题的综合度较高,常规解题思路是利用导数的几何意义,先假设切点,根据切点的坐标满足曲线的方程、切点在切线上,以及切线的斜率等于曲线所对函数的导数在切点处的值来进行求解.有时要注意“在”跟“过”这两个字眼的区别:对“在某点处的切线”,此点是切点;对“过某点的切线”,此点未必是切点(但也可能包括前一种情形). (1) 无参数情形 例3已知函数f(x)=xlnx+2,若直线l过点Q(0,1),并且与曲线y=f(x)相切,则直线l的方程为______. 解点Q显然不是切点,设切点P(x0,y0),则 y0=x0lnx0+2. ① 又f′(x)=lnx+1,由kPQ=f′(x0),得 ② 联立① 与②,解得x0=1.从而切点P(1,2),切线斜率f′(x0)=1,可得切线l的方程为y=x+1. 例4已知函数f(x)=x3-3x+1,若直线l过点Q(2,3),并且与曲线y=f(x)相切,则直线l的方程为______. 解计算知点Q在已知曲线上. 若点Q是切点,由f′(x)=3x2-3,易得直线l的方程为y=9x-15. 综上,l的方程为y=9x-15或y=3. 评注由例2知直线与曲线相切时,直线与曲线不一定只有一个交点.因此,对于直线过某点与曲线相切的问题,在切点不明确时,必须对该点进行分类讨论. (2) 含参数情形 例5若直线y=x+a是曲线y=xlnx+1的切线,则实数a的值为______. 解设直线l与f(x),g(x)图象的切点分别为P(x0,y0),Q(x1,y1),则y0=x0+ex0,f′(x)=1+ex. 若x1=1同理可得出矛盾,从而x0≠1,x1≠1. ③ ④ x0=a-x1. ⑤

二、直线与二次曲线相切的问题



三、直线与非二次曲线相切的问题


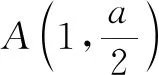
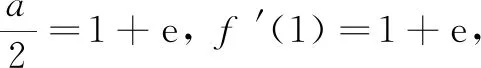


四、 综合问题举例