强磁对空间带电粒子环境影响研究

2020-10-31尚逸帆王义元黄朝艳

载人航天 2020年5期

尚逸帆，赵展，王义元，黄朝艳，王爽

(1. 上海宇航系统工程研究所，上海201109； 2. 南京航空航天大学航天学院，南京210016)

1 引言

目前常规遥感卫星、导航卫星、通信卫星自身磁场远低于1T 量级，常规卫星电磁兼容(Electromagnetic Compatibility Design， EMC)设计也未对强磁环境做针对性考虑。随着电磁技术在航天领域的广泛应用，越来越多具有强电磁特性(强度达到1 T 量级)的载荷运用于空间任务中。例如，在轨服务飞行器采用强电磁对带磁性碎片吸附[1-2]，执行碎片清除任务；自身有较强磁场的质谱仪可用于空间环境分析[3]；100 kW 级以上核动力航天器与大功率电推力器组合使用，可执行空间往返运输任务；大功率磁等离子体推力器工作实现轨道转移，同时也会产生强磁场[4-5]。上述载荷工作时均产生强磁场，中心磁场可以达到1 T量级，对空间带电粒子传输轨迹产生影响，同时也改变了卫星在太空环境下受辐照特性。

国内外针对空间辐射防护有长期研究[6]，主要辐射源有地磁捕获辐射、太阳粒子辐射以及宇宙射线等，由于传统应用卫星本身磁场较弱，在卫星辐射防护设计中，只需要考虑空间本底辐射环境。在此基础上，邓佳欣等[7]对磁力矩器工作时磁场效应进行分析，由于其磁场相对较弱，磁力矩器磁场使1 keV 以下的带电粒子产生不均匀分布，这种不均匀分布导致局部材料带电，对辐射防护几乎无影响。

针对带有强磁特性卫星的空间辐射防护问题，在传统防辐射措施的基础上，本文重点研究空间带电粒子在强磁载荷作用下的通量变化，通过建立模型并仿真计算，定量分析带电粒子通量在卫星不同位置变化率，明确通量增加显著区域。

2 强磁对带电粒子影响模型

2.1 粒子运动模型

带电粒子在磁场中主要受洛伦兹力作用，描述方程为式(1)、式(2):

式中，m 为粒子质量，q 为粒子电荷量， v 为粒子在磁场中的运动速度， r 为粒子在磁场中的位置，B 为卫星产生的强磁场。

由于卫星本身载荷工作产生的磁场达到1 T量级，且磁场厚度较小，地球磁场强度约为50 ～60 μT，比强磁载荷低4 个数量级以上，因此研究强磁载荷影响时可忽略地磁场。

2.2 粒子入射分布模型

空间辐射环境主要包括辐射带电子、质子、宇宙射线粒子以及太阳耀斑质子等[6，8]。按照粒子入射方式不同，分别提出各向同性入射和定向入射模型。

采用蒙特卡洛方法模拟入射粒子源，使用随机数ζ1，2⊂ 0，1[ ] 来定义球面上初始入射粒子的随机位置和速度分量，用来描述带电粒子从各方向等概率入射目标区域， v 表示入射粒子的速度值，θ 表示速度矢量与z 轴的夹角，φ 表示速度矢量在xOy 平面的投影与x 轴的夹角。描述方程为式(3)、式(4):

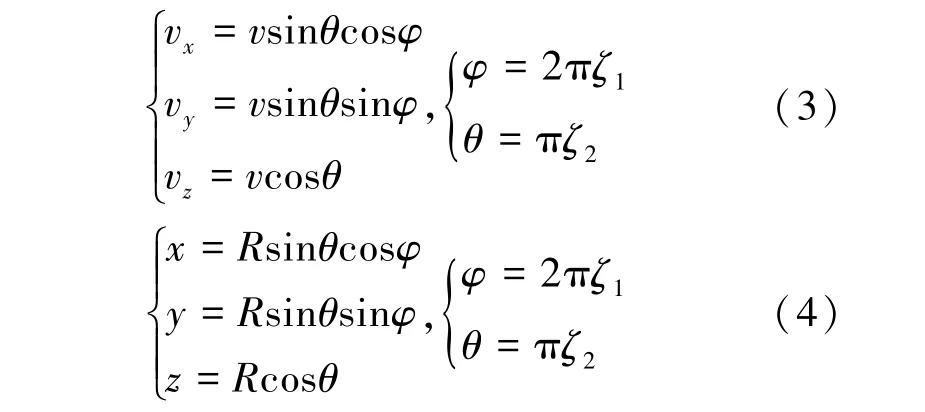
速度坐标表示为 v，φ，θ{ }，位置坐标表示为{ R，φ，θ}。

图1 为利用蒙特卡洛方法模拟粒子源入射区域情况，粒子源入射模型呈各向同性分布。

图1 蒙特卡洛方法模拟各向同性入射粒子源Fig.1 Monte Carlo simulation of isotropic incident particle source

针对定向辐射特性建立模型，入射方向具有确定，入射位置具有随机性。同上，使用随机数ζ1，2⊂ 0，1[ ] 来定义球面上初始入射粒子的随机位置分量和入射速度，用θ0和φ0来描述定向辐射方向与坐标轴的夹角。速度大小用v 表示，为随机变量。描述方程为式(5)、式(6):

速度坐标表示为 { v，φ0，θ0}，位置坐标表示为 R，φ，θ{ }。

2.3 磁场影响评价模型

为有效评价磁场对带电粒子分布或能谱的影响，采用Hoffman 使用的方法[9]，即通过无磁场与有磁场进入指定区的带电粒子数来评价作用效率。磁场影响评价指数为式(7):

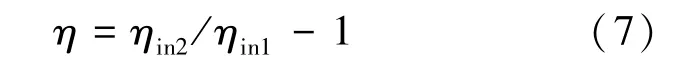
式中，η 表示通量增加率， ηin2和ηin1分别表示有磁场和无磁场时进入指定区域的粒子数。η ＞0 表示粒子通量增加， η ＜0 表示粒子通量减少。

由于粒子电荷质量比不同，在磁场中的转弯半径不同。因此，对同种粒子中不同能量的粒子进行统计，ηin2(β) 和ηin1(β) 表示能量为β 的粒子在有无磁场的粒子数统计， A(β) 为能量为β的粒子在入射粒子中所占的比例。对粒子不同能谱分别计算作用效率，并按所占比例加和，得到同种粒子中不同能量的综合作用效率，如式(8)所示:

3 粒子受磁场影响分析

根据任务和载荷的不同，卫星自身产生的强磁场不同。以卫星包络内部的柱形磁场为例进行分析。强磁场影响范围外径为1 m，高度为0.5 m，磁场分布呈轴对称，中心位置磁场强度最强，可达1 T以上。

磁场对空间粒子能谱的影响实际上是对单个粒子影响的集体效应。带电粒子在磁场中的运动特性，与带电粒子参数(质量、电荷、能量)和磁场分布有关。首先，从微观角度讨论磁体磁场作用下的典型粒子(电子、质子和重离子)运动轨道特性；然后，分析磁体磁场作用下典型能谱(辐射带电子、质子能谱和银河宇宙线重离子能谱)的变化规律[10]。

3.1 电子运动轨迹影响

取入射位置和方向相同，能量分别为0.1 MeV和1 MeV 的辐射带电子，射入中心场强为1 T的柱形磁场，对其运行的轨迹进行分析，如图2 所示。

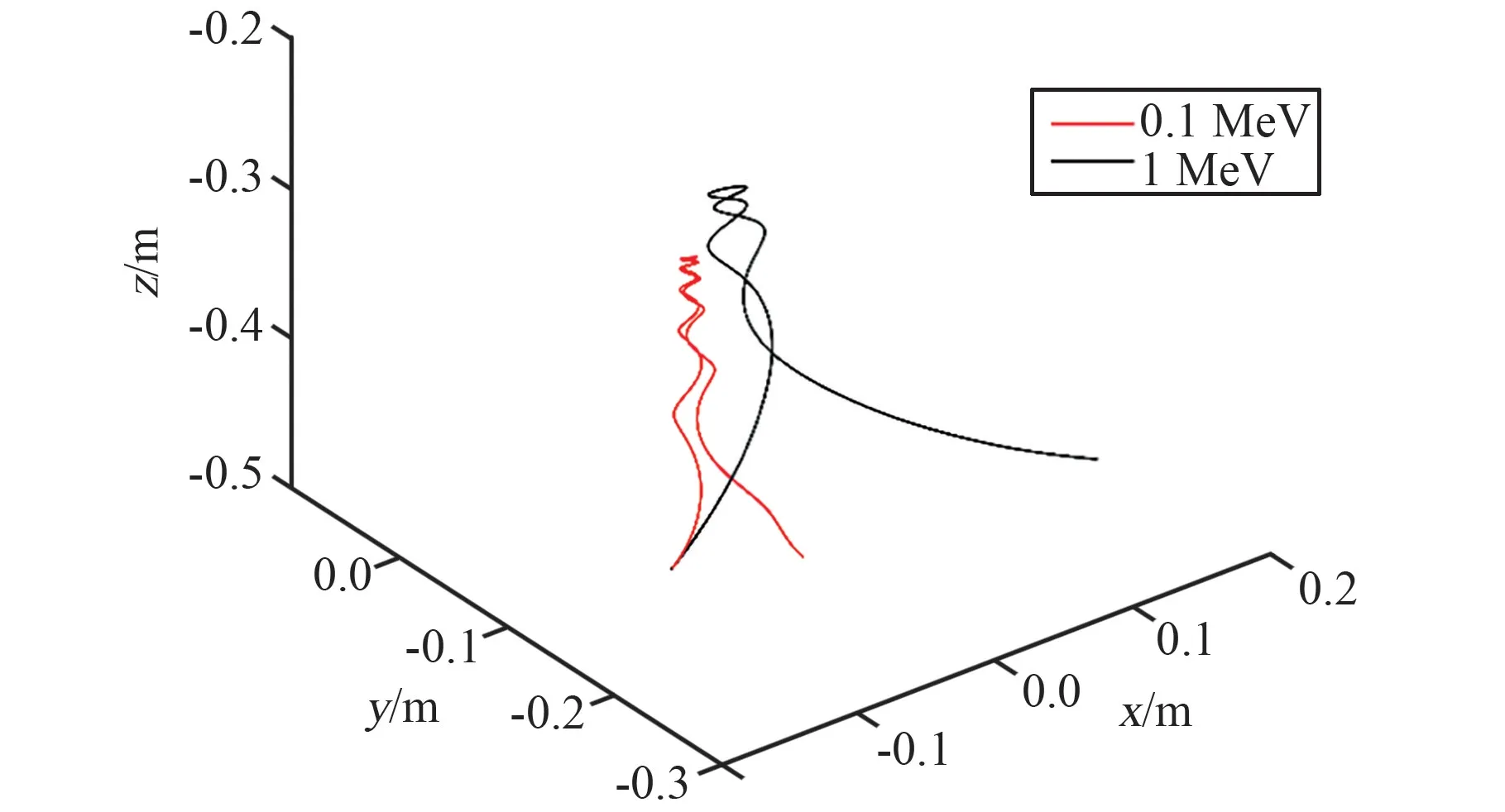
图2 0.1 MeV 和1 MeV 电子在磁场中的运动轨迹Fig.2 Trajectories of 0.1 MeV and 1 MeV electrons in the magnetic field

电子在弱磁区偏转角度较小(轨道半径大)，在强磁区因大角度偏转而产生回旋运动，0.1 MeV电子的轨道半径较1 MeV 电子的轨道半径小，即低能电子轨道受磁场偏转作用更大，且主要发生在强磁区。可以判断，在中心磁场达到1 T量级的强磁环境下，0.1～1 MeV 的电子都有较为明显的偏转。

磁体磁场形成的强磁区，对低能电子还存在强束缚作用，以入射能量为0.04 MeV 的电子进行仿真，如图3 所示。图中可以看出:以某个角度进入到强磁区的能量为0.04 MeV 辐射带电子，强磁环境对其形成束缚，使其长时间在强磁区内保持循环运动。

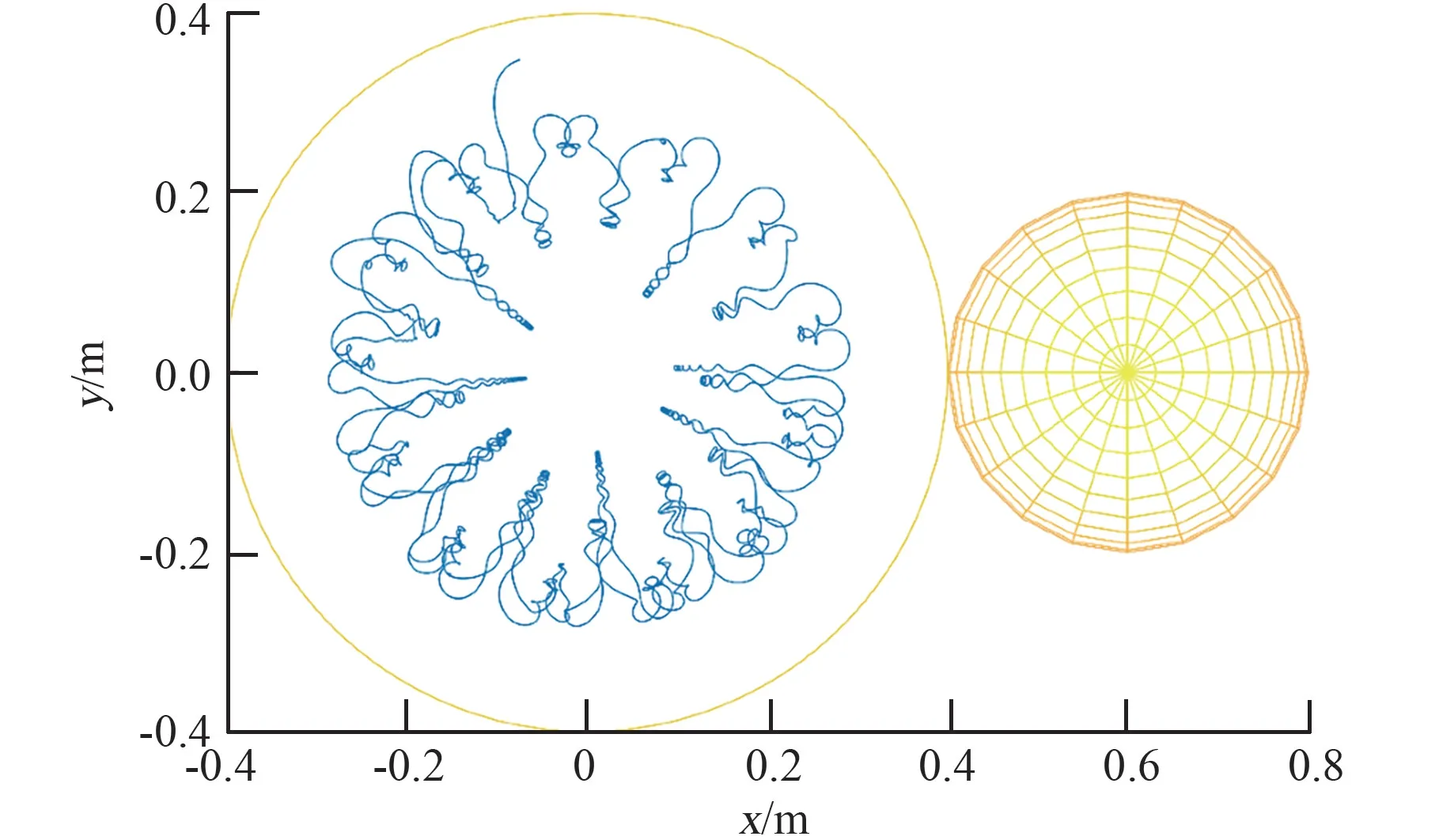
图3 0.04 MeV 电子被强磁场束缚Fig.3 The 0.04 MeV electrons bound by the magnetic field

3.2 质子和重离子运动轨迹影响

取入射位置和方向相同，能量分别为0.1 MeV和1 MeV 辐射带质子进行测试，如图4所示。图中可以看出:0.1 MeV质子仅在强磁区有小角度偏转，1 MeV质子轨道近似直线，基本不受磁体磁场影响。由于质子质量相对较大，在1 T量级的磁场环境下，0.1～1 MeV 的质子传输路径基本不受影响。

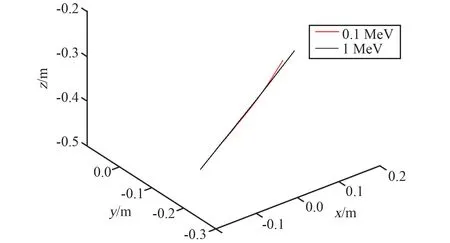
图4 0.1 MeV 和1 MeV 质子在磁场中的运动轨迹Fig.4 Trajectories of 0.1 MeV and 1 MeV proton in the magnetic field

取入射位置和方向相同，能量分别为0.1 MeV和1 MeV 银河宇宙线He 粒子进行测试，如图5 所示。图中可以看出:0.1 MeV 和1 MeV的He 粒子受磁场影响较小，运动规律与质子相似，其偏转半径更小。

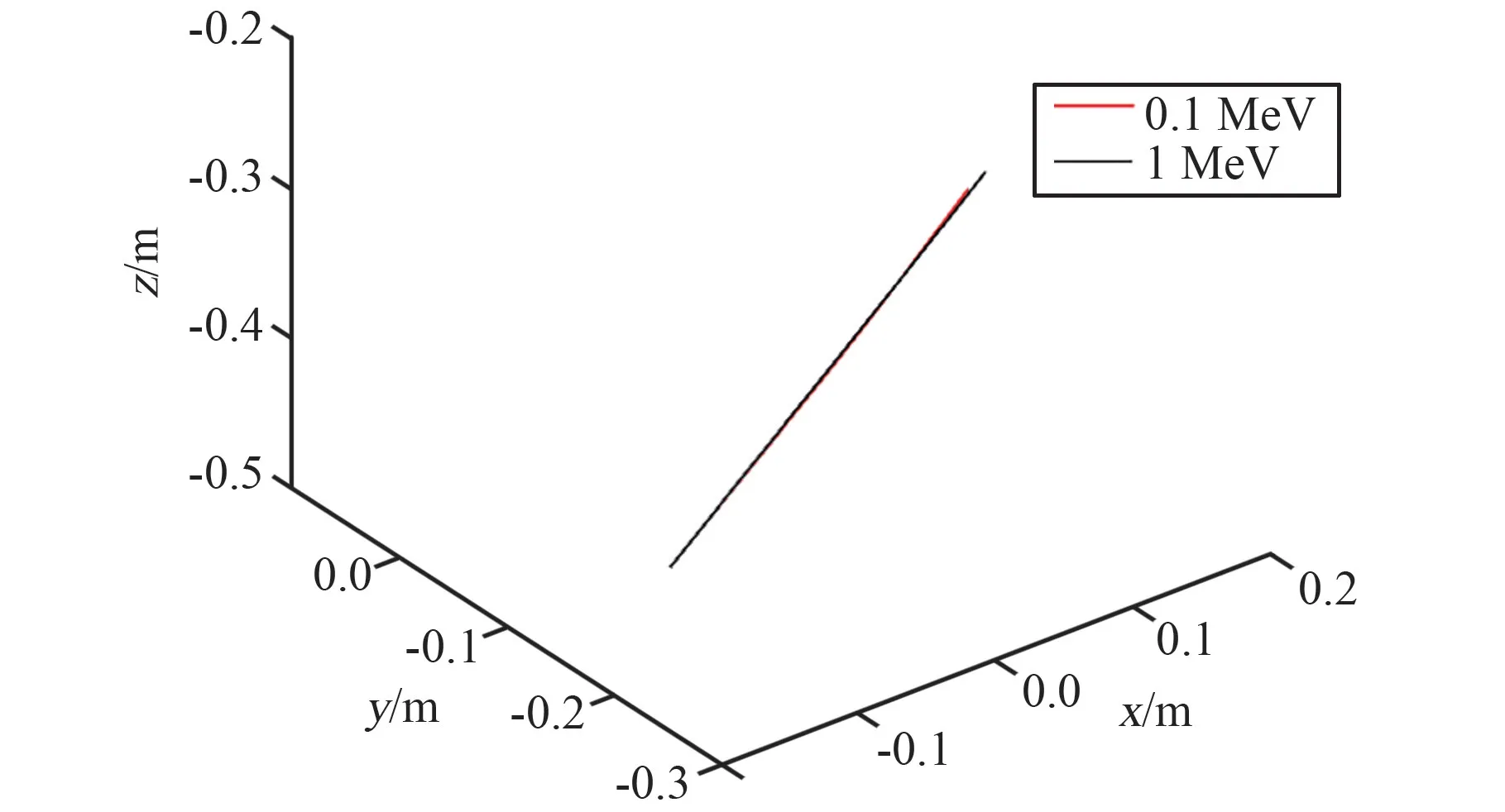
图5 0.1 MeV 和1 MeV He 粒子在磁场中的运动轨迹Fig.5 Trajectories of 0.1 MeV and 1 MeV He ion in the magnetic field

3.3 典型粒子在磁场中的运动影响分析

磁体磁场对低能段粒子产生影响较大，相同能量下，电子受磁场影响的偏转角远大于质子和重离子。质子和重离子受磁场影响比较微弱，0.1 MeV能级的质子和重离子传输仅产生微小偏转，1 MeV 及以上能级的传输几乎无影响。

4 典型粒子能谱影响分析

分别针对辐射带、太阳耀斑及宇宙射线中的典型粒子进行分析。以测试区位于磁场中心为例，分析磁体磁场对半径为0.2 m 的球体测试区内粒子能谱影响。

4.1 对电子能谱影响分析

辐射带电子主要分布在近地球空间，能量分布主要在0.04～7 MeV 之间。以测试区中心处磁体磁场对电子能谱的影响进行分析。

在磁体中心处，磁体磁场影响下，低能段辐射带电子微分通量呈大幅度下降，能量1 MeV 以下的电子微分通量下降高达30%以上，如图6 所示。图中可以看出:即使在低能段，被磁场束缚的比例仍然很低，可以忽略其影响。

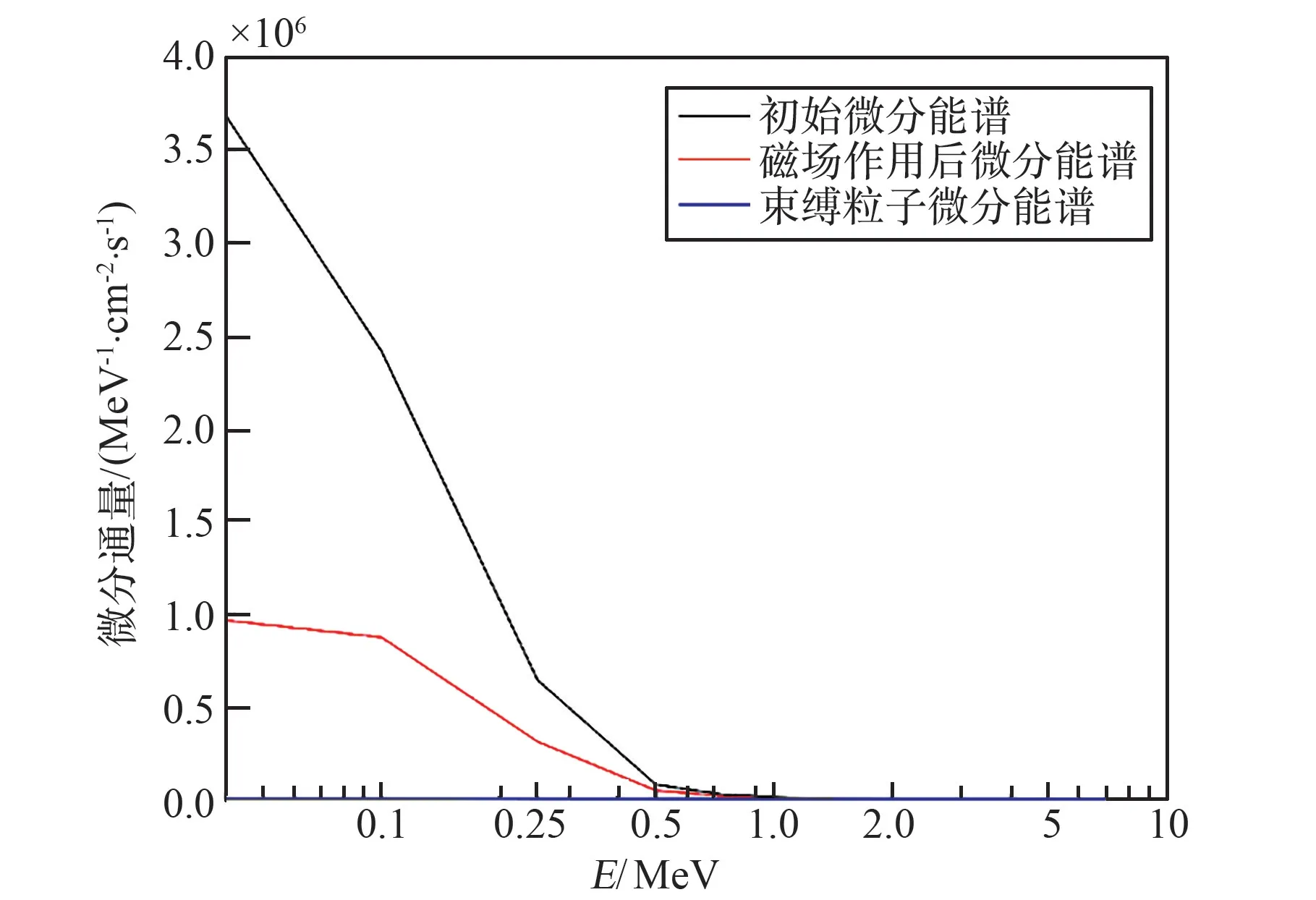
图6 磁体中心磁场对辐射带电子能谱影响Fig.6 Effect of magnetic field in the center of magnet on electron energy spectrum of radiation belt

4.2 对质子能谱影响分析

质子主要包括辐射带质子、太阳风产生的质子以及宇宙射线产生的质子。由于宇宙射线中质子能量较高，可以忽略其通量受强磁场的影响。具体如下:

1)辐射带质子:辐射带质子能量分布在0.1～300 MeV。在磁体中心处，辐射带质子初始微分能谱和磁体磁场作用后的微分能谱重叠在一起，表明磁体磁场对辐射带质子能谱基本没有影响，0.1 MeV 质子微分通量下降最大3.46%，整个能谱通量减少率1.53%。可以判断质子运动受磁场影响很小，磁场对质子能谱影响如图7 所示。

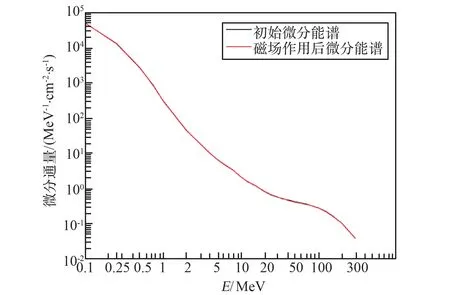
图7 磁体中心磁场对辐射带质子能谱影响Fig.7 Effect of magnetic field in the center of magnet on proton energy spectrum of radiation belt

2)太阳耀斑产生的质子:太阳耀斑产生质子呈定向辐射，考虑其入射方向不定，采用同性辐射源进行分析。磁体磁场对太阳耀斑能谱和通量基本没有影响，如图8 所示。

图8 磁体中心磁场对太阳耀斑质子能谱影响Fig.8 Effect of magnetic field in the center of magnet on solar flare proton energy spectrum

3)宇宙射线产生的质子:宇宙射线中，中低能段粒子所占比例极低，相比高能段低6 个数量级以上，粒子能量主要分布在1 MeV～10 GeV，如图9 所示。

4.3 对重离子能谱影响分析

重离子主要来源于宇宙射线，其能量分布于宇宙射线中的质子分布类似，粒子能量主要分布在1 MeV ～10 GeV，如图10 所示。图9、图10 比较可以得出:宇宙射线重离子峰值区域通量密度比宇宙射线质子通量密度大约低一个数量级。

图9 宇宙射线中质子能谱分布Fig.9 Effect of magnetic field in the center of magnet on cosmic ray proton energy spectrum

图10 宇宙射线中重离子He 能谱分布Fig.10 Distribution of heavy ions He in cosmic ray

重离子初始通量与磁场作用后的通量曲线基本一致，如图11 所示，可以得出:空间重离子受磁场影响较小。且在宇宙射线中，1 MeV 以下重离子比例极低，可以判断，在宇宙射线中重离子通量变化基本不受卫星产生磁场影响。

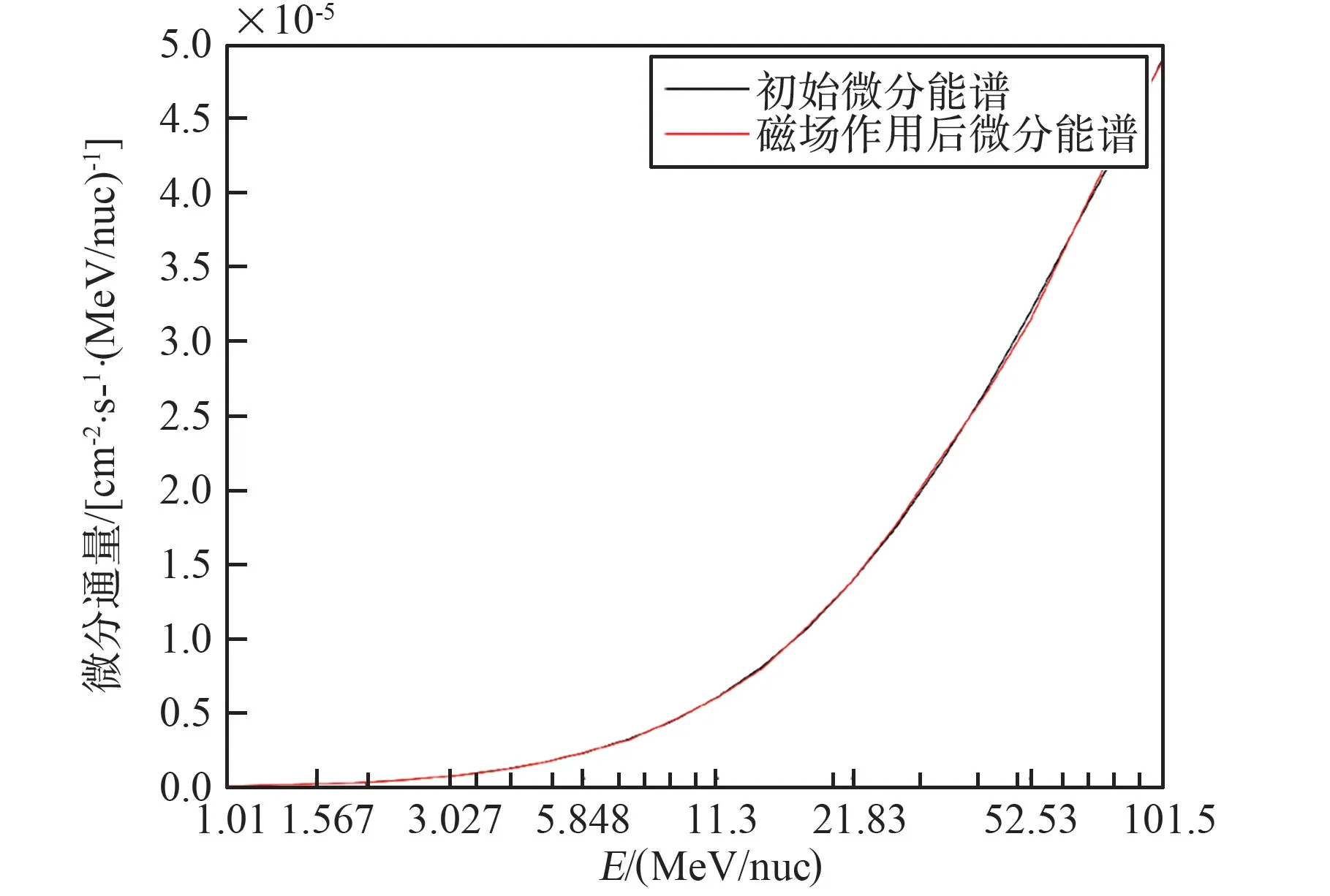
图11 磁体中心磁场对宇宙射线He 能谱影响Fig.11 Effect of magnetic field in the center of magnet on cosmic ray He energy spectrum

4.4 典型粒子能谱在磁场中作用的初步分析

针对辐射带、太阳耀斑、宇宙射线中的几种典型粒子进行初步分析。可以得出以下结论:

1)电子在辐射带中的能量较低，主要在1 MeV以下，且电子受磁场作用较强，其通量变化率较明显；质子运动状态受磁场影响较小，即使0.1 MeV 质子通量的影响变化也不超过5%。

2) 针对 0.1 MeV 能量以下的质子和0.04 MeV能量以下的电子通量密度较大，能量较低，几乎无法穿透卫星蒙皮或电机壳体，不会影响卫星辐射总剂量。但大通量密度的电子和质子可能会导致局部电荷累计而导致静电放电，可采用良好的接地设计、避免孤立导体等措施防护，不需特殊防护，本文不再深入研究。

3)重离子运动状态受磁场影响较小，且通量占比高的粒子主要分布在1 MeV ～10 GeV。因此，从工程角度出发，可以忽略重离子通量变化率受磁场影响。

4)辐射带质子和电子受到磁场俘获而产生方向性，且质子和电子方向异性。但卫星在轨运行时，每个轨道周期都存在一次南北方向的往复运动，且姿态指向与地磁场方向无特定关联。同时考虑带电粒子穿透卫星所产生的的电离效应、位移效应以及单粒子效应均具有随时间所累加的总剂量效应特点，因此，从长期在轨分析，对辐射带的质子和电子分析采用各向同性入射的粒子源模型。

综上，本文仅对辐射带电子能谱在磁场中的作用开展研究，对卫星各单机全寿命周期的辐射总剂量分析采用各向同性模型。

5 不同测试区受辐射带电子影响分析

根据典型粒子能谱在卫星产生强磁场作用下的通量变化率分析得出:辐射带电子是主要受影响的粒子。下面以磁场中心为原点，典型卫星的几个重要单机布局位置坐标作为测试区，分析辐射带电子通量变化(图12)。

5.1 试验测试区选择

以典型卫星布局为例，重点针对星敏、光电设备、仪器板等重要敏感单机设备位置[11]，设置9个测试区，测试球半径0.2 m。具体如下:O 区(0，0，0)，A 区(0.68，0，0.2)，B 区(0.6，0，0.4)，C 区(0.64，0，1.6)，D 区(0.75，0，1.5)，E 区(0.55，0，2)，F 区(0.9，0，2.2)，G 区(0.7，0，-1.7)，H 区(0.45，0，0)，坐标单位为m。

地磁场强度约为5×10-5T，卫星载荷工作产生的磁场强度达到1 T 以上，忽略地磁场影响。

5.2 测试仿真

根据粒子运动模型模拟粒子在磁场中轨迹，利用蒙特卡洛方法模拟入射粒子源。强磁场影响范围外径为1 m，高度为0.5 m，磁场分布呈轴对称，中心位置磁场强度最强，可达1 T 以上。入射粒子束取50 万，分别针对选择的9 个测试区进行无磁场和有磁场环境下的仿真，根据磁场影响评价模型分析入射电子通量变化。

从9 个测试区的数据可以看出，不同测试区域辐射带电子受到有不同程度磁体磁场影响，如图12 所示，可以得出:磁体磁场中心最强，多数电子被磁场而偏转，测试区O 电子通量降低了约60%；A、B、C、D、E、F、G 处，辐射带电子通量均有所增加，其中D、G 测试区整个能谱通量增加率超过10%，但不超过15%；所有测试区对电子束缚率都很低，被束缚电子数量不超过入射粒子总数的0.1%。