一种可变车长的元胞自动机交通流模型
2020-10-30应新洋何超杰周国兵
应新洋 何超杰 周国兵

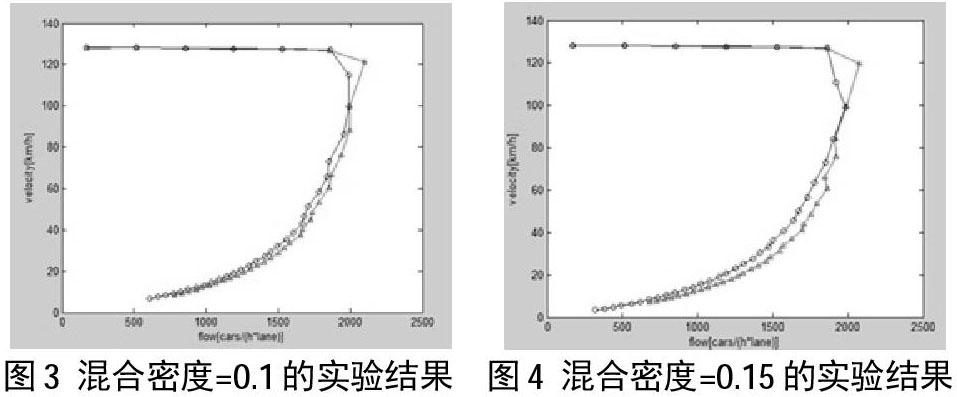
摘 要:在一维元胞自动机交通模型NaSch的基础上,提出了一种改变车辆长度来模拟混合交通流的元胞自动机交通流模型,模型考虑了交通流中大小车混合情况,并引入了车长、元胞尺寸、车辆安全间距等概念,通过元胞长度来设置不同的车辆长度,从而模拟交通流。数值模拟表明:这种可变车长的CA模型能更好的模拟实际交通情况的一般特征;不同车长的混合交通流时,大车对交通流量有一定的影响,混合密度越大对交通流的影响越大。
关键词:元胞自动机;可变车长;交通流
1 引言
随着经济和社會的发展,城市规模不断扩大,车辆保有量不断增加,交通出行问题越来越突出,并受到特别关注。交通问题的研究和解决成为城市发展过程中必须解决和改善的问题,研究交通问题,建设智能交通系统,尤其是实现交通流量的模拟、分析、控制、诱导具有现实的背景和意义。交通系统本质上是一个离散的复杂系统,具备很多非线性的特征,而元胞自动机动力学模型本质上也是离散的,它通过比较简略的微观规则来反映宏观交通现象,在描述实际交通现象时具有独特的优势,通过研究元胞自动机的理论并将其应用到城市交通的流量分析和控制中具有重要的意义和实际应用价值。交通流的非线性、复杂性和离散性与元胞自动机的特性相符合,因此国内外学者将元胞自动机模型广泛应用于交通流的研究。
2元胞自动机交通流模型[1-3]
元胞自动机,简称CA,物理学中指在离散的状态下,将元胞在元胞空间内,运用合理的、局部的规则,进行演化展示的一种动力学系统,其中元胞和时间都是离散有限的。元胞自动机主要构成部分:元胞、元胞空间、邻居和演化规则。随着元胞自动机应用推广,交通流的模拟和应用成为最主要的应用场景之一。
1986年,Wolfram提出了最初的元胞自动机交通流模型CA184号规则,1992年Nagel和Schreck Enberg在CA184号模型的基础上,提出了一维元胞自动机的NaSch模型,模型中所有的车辆都被统一设置成一个元胞长度,考虑了车辆的加速、减速、随机延迟和车辆位置的更新,较好的模拟了车辆的实际情况,得到了广泛应用。许多科技工作者在NaSch模型基础上,做了大量的工作,提出了很多改进的方法和措施,建立了基于NaSch的各种元胞自动机交通流模型,这些模型多为对相同长度的车辆构成的交通流进行研究,而在实际的道路交通中,交通流是有大车、小车等混合车流所组成的,车辆的长度是不一样的,即使是小车,不同的小车之间的长度也是不一样的,比如A车车长约为5米,B车车长约为7.5米,B车车长约为15米,这些长度不一的车辆混合在一起,统一设置成某个长度来模拟,会存在一个较大的误差。因此,本文考虑改变车长和元胞的尺寸,更好的模拟和分析车辆实际情况。
3 一种可变车长的元胞自动机交通流模型
基于车辆和元胞统一长度带来的问题,本文在NaSch模型上,考虑根据改变车长和元胞尺寸来模拟交通流。为方便问题描述,本文讨论最简单的一种情况。
设有车辆Car1和Car2,车长分别为L1和L2,元胞尺寸为L,则有:
L=GCD(L1,L2)
GCD是取最大公约数,即元胞尺寸为L取L1和L2的最大公约数。
L1=K1*L,L2=K2*L,其中K1、K2为整数,即车长为整数倍个元胞长度。
例:车辆Car1和Car2,L1=7.5,L2=15,则L= GCD(L1,L2)=7.5,元胞尺寸和车辆的某个状态可以用图1表示。
模型中,道路被划分为若干个离散的元胞,每个元胞要么是空的,要么被车辆占据,每辆车的速度取 0,1,2,…vmax,vmax是最大速度。运行过程中,即时间 t à t +1 的过程中,车辆状态变化的算法(元胞更新算法中要注意车辆的整体性移动和位置更新,如图1 中Car2移动时必须作为整体更新。)如下:
STEP1:vnàmin(vn +1,vmax); //加速
STEP2:vn àmin(vn,dsafen+ dn -1);// 减速
STEP3:vn àmax(vn -1,0); //以概率 p 随机减速
STEP4:xn àxn +vn。 //位置更新
其中vn、xn 分别表示第n辆车的速度和位置,dn =xn +1 -xn-1表示第 n +1 辆车和第 n 辆车的间距,dsafen表示第 n +1 辆车和第 n 辆车的安全间距,主要和车辆的速度有关,本文采用dsafen=k*vn,k为常量。随机慢化概率 p用来描述实际交通中的随机因素。
第一步应用加速规则,表示车辆状态将加速行驶,逐步达到最大限速,如果如果车间距足够大,当前车辆可以达到 vmax;
第二步应用减速规则,为了避免撞车,驾驶员考虑车辆的速度、位置、与前车的安全间距,确定性减速;
第三步随机减速规则,为了描述实际交通中的随机因素,用随机慢化概率 p来减速,减速规则同第二步。
第四步位置更新规则,车辆位置更新,在更新的过程中要注意,部分车长大于元胞尺寸的车辆,在移动的过程中是一起移动的,不可分离。
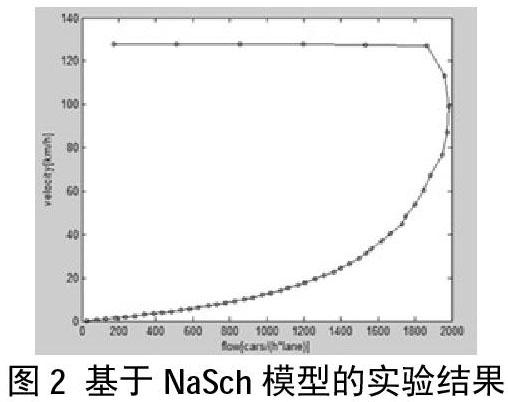
4模型实现及实验结果
本文实验采用周期性边界条件,初始模型有1000 个元胞组成,元胞尺寸为7.5m,单位时间步长t为1s,最大速度 vmax =5;对应实际道路长度LR=7.5km,实际车速为 vmax =135km/h;N是分布在LR上的车辆总数,则车辆密度 ρ=N/LR,t 时刻空间平均速度定义为:V(t)=(1/N)∑(vi(t)),平均车流量为 q =ρV。安全车间距dsafen=k*vn中的k=0.5,随机慢化概率 p=0.25,车辆初始密度 ρ=0.01,每次增加0.01,一直到ρ=1为止,然后统计车辆运行的平均速度和交通流量。
