应用题解决的心理学研究及其对中学数学教学的启示
2020-10-30吕立夏喻平
吕立夏 喻平
摘要:应用题解决的心理学研究主要集中在问题表征、情境因素、解题策略、模式识别、元认知及非智力因素对应用题解决的影响等方面。将相关研究成果应用于中学数学应用题教学,可以提炼出几点策略:丰富领域知识,形成扎实基础;加强审题训练,提升表征水平;构建变式问题,促进知识迁移;设计自我提问单,提高监控技能。
关键词:应用题解决 领域知识 问题表征 模式识别 元认知
应用题解决是数学学习的难点,因而成为心理学研究关注的问题。应用题解决的心理学研究主要集中在问题表征、情境因素、解题策略、模式识别、元认知及非智力因素对应用题解决的影响等方面。本文对相关研究做简要介绍,并由此提出中学数学应用题教学的几点策略。
一、心理学对应用题解决的一些研究
(一)问题表征
问题表征是指通过审题,明确给定的条件、目标和允许的操作,检索、激活头脑中与之相关的知识和经验,将外部的物理刺激转化为内部心理符号,形成问题空间的过程。西蒙认为,问题表征是问题解决的一个中心环节,它说明问题在头脑中是如何表现出来的。有时候问题解决的难度并不在问题本身,而在于解题者对问题表征的方式。
问题表征是一个逐步深化的过程。傅小兰等就一道应用题对34名学生进行测试,通过分析被试的解答,得出被试对问题进行表征、建立问题空间的一般过程。第一,问题信息的搜索和提取。在这个过程中,解题者需要从问题陈述中、长时记忆中提取全部有关信息;一旦搜索问题信息时遗漏了某些信息,建构的问题空间就不完整,也就无法求得问题的正确解。第二,问题信息的理解和内化。在这一过程中,解题者需要对搜索和提取的问题信息做深加工,从而正确地理解和利用问题信息,发现问题的结构,构建自己的问题空间。第三,发展隐喻约束条件与意识化,即对问题规则(约束条件)的理解和掌握在构建正确的问题空间中起着重要的作用。问题表征过程中的任何环节出了差错,都将导致构建出错误的或不完整的问题空间。因而,正确的问题表征是解决问题的必要前提。
Mayer依据提取信息的不同将问题表征划分为数字表征、关系表征、图式表征三种类型。数字表征指依据问题中的数字关系理解问题;关系表征指依据问题中的变量关系理解问题;图式表征指依据问题的内在结构理解问题。有学者依据问题的表征形式对问题做分类:(1)字面特征分类,即依据题目的文字描述而非从数学角度做出的分类(例如,把题目内容是食品的归为一类);(2)表层结构分类,即依据题目的表面信息而非从数学本质角度做出的分类(例如,把题目内容是路程问题的归为一类);(3)深层结构分类,即依据题目的数学本质做出的分类(例如,把有关路程内容的问题分为追击问题、相遇问题等)。冯虹等的研究表明,随着年级的增高,学生越来越倾向于按照题目的深层结构分类,数学成绩优秀生与差生分类的结果差异显著。
问题表征离不开对信息的搜索和提取,离不开专门知识(也就是领域知识)的支持。有研究表明,领域知识不同的学生在问题表征过程中具有不同的特点:领域知识丰富的学生更倾向于深层次表征问题,而领域知识贫乏的学生更倾向于浅层次表征问题。也就是说,如果学生头脑中具备丰富的公式、定理、问题原型和应用题模式,那么其更倾向于对问题做深层次表征,从而正确地解决问题。张维的研究也证实了这个结论。研究采用“学习—再认”范式,研究学科领域知识丰富性不同的学生(依据数学学业成绩分类)在问題表征层次上的特点。“学习—再认”是指让被试先学习一个材料,然后进行测试,判断测试题中是否出现了前面学习过的东西,包括表面特征和原理特征。结果表明,“知识丰富组”表征问题除了采用表面特征外,还会对原理特征进行表征;“知识贫乏组”为避免干扰,会丢弃原理特征,往往用表面特征来识别问题。
(二)情境因素
应用题的表述往往是有情境的,那么情境是否会对问题解决产生影响?不少学者对此进行了研究。Zhang通过“TicTacToe”式同型游戏问题发现,问题的外部结构与情境不仅是对内部意识的输入和刺激,而且具有独立于内部表征的作用,就此提出了问题的外部表征概念。他认为,外部表征是指问题情境的成分和结构,外部表征的信息只能被知觉系统察觉、分析和加工。邢强等通过对相关文献的整理、分析,提出数学应用题的外部表征影响因素主要包括文本表面特征、文本内容熟悉程度、符号、插图、问题与文本的呈现位置、不同的措辞、情境内容的现实性等。
赵继源基于一道零分率超过60%的高考数学试题——“冷轧机”应用题,设计了6道对比应用题,对高二学生展开测试。结果发现,应用题背景的熟悉程度对学生解题有显著影响;对于背景熟悉的题目,数据抽象与否对解题影响不显著,但在陌生背景下则达到了显著水平;对于背景陌生的题目,即使凸显关键信息,其影响也不明显。他还进一步发现,对于中等或中下水平的学生而言,凸显关键信息对于解题不会有任何帮助,但对于数学基础较好的学生,凸显关键信息对于解题有明显的启发作用。
章巍将代数应用题的语言描述特征分解为语量、语境、语序和关键词的隐蔽程度四个指标,通过实验逐一研究每个指标与解题效果的关系。结果表明:语量对初二学生解答代数应用题效果的影响明显,“学困生”相对于“学优生”更容易受语量的影响;语境对解答代数应用题效果的影响明显;语序对解答代数应用题的效果有一定程度的影响,但不够显著;关键词的隐蔽程度对解题结果有一定程度的影响,但不够显著,而对解题时间的影响却非常显著,即大多数学生面对关键条件隐蔽性较强的代数应用题时,会花费大量时间去寻找和发掘这些条件。
情境内容的真实性是指数学应用题的背景是真实存在的。一些学者据此定义了规则应用题和不规则应用题:规则应用题即传统的应用题,题目规范,条件充分,答案唯一;而不规则应用题由于背景真实,条件可能多余,也可能不足,答案可能无解,也可能有多解。学生解决不规则应用题时,不仅要结合数学知识,而且要基于日常生活经验。Sweller等提出的认知负荷理论可以解释为何有多余条件的应用题对学生来说是最难的。该理论认为,在解决有多余信息的问题时,解题者必须对两种信息进行加工,即正确解题所需的信息以及多余信息;解题者首先需要集中精力来区分这两种信息,然后才能对解题有关的信息进行充分的表征。
冯虹等用眼动分析法分析不同年级学生对不同类型题目(完整的、有多余条件的、缺少条件的和缺少问题的题目)的表征层次和解题策略。结果发现:不同年级学生对“题设”的相对注视次数(被试在某个兴趣区的注视次数占全部注视次数的百分比)的差异并不显著,但是对“关键信息”的相对注视次数则表现出了明显的年级特征;学生解规则题目时对“题设”的相对注视次数非常显著地小于不规则题目,解不规则题目时对“关键信息”的相对注视次数显著大于规则题目。实验还发现,学生解缺少条件的题目时正确率最高,原因在于学生对题目进行深度表征后,会添加一些很容易解答的条件或问题;而解有多余条件的题目时正确率最低,说明有多余条件的题目对学生而言最难解决。
(三)解题策略
解决应用问题有一些策略(最常用的就是画图策略)。信息区分策略是指在解题过程中将题目背景及问题分析成语义单元,对信息类型进行检验、区分,找出信息之间的相关性,目的是对这些信息进行比较,进而与问题相匹配。Littlefield等通过观察学生的眼动轨迹,发现学生一共使用了5种区分策略。(1)重读题目策略:通过重复地阅读题目,将部分信息及语义特征贮存到工作记忆中,然后对信息进行比较。(2)单一比较策略:在数字及关系词之间进行简单、直接的比较,可能会根据问题部分的要求直接列出方程。(3)以特征为基础策略:在题目中寻找与问题部分的语义特征相匹配的语义特征,通常会将注视点集中在变量名或与问题部分相似的事件、概念上。(4)“问题—引导”策略:以问题部分的语义特征为指导,对信息进行分析。(5)首次读题区分策略:对语义类型进行区分,找到解题所需的关键信息,将注视点集中在关键信息和相关数字信息上。岳宝霞等以初二学生为被试,采用眼动分析法探讨了题目难度、冗余信息和数学成绩对学生采用信息区分策略的影响,结果证实了学生解答应用题存在上述5种策略。
人们关注的另一个问题是,能力水平不同的学生是否会采用不同的策略解决问题。张锦坤等运用作品分析法分析初二优秀生、中等生和差生对两道中等偏上难度几何应用题的解答情况,以此探讨各层次学生解答应用题的策略类型。分析发现,不同水平的学生在两道几何应用题的解题过程、解题步骤上所使用的策略是不同的:优秀生的解题策略为“俯瞰型”,他们能深刻理解问题,通过不断创造中间条件灵活连接条件与问题的关系;中等生为“经验型”,表现为过度依赖过去的解题经验,对问题与条件之间关系的综合把握不够灵活;差生为“盲目型”,表现为对解题的目的指向性不强,只是试探性地从已知条件中推导出一些结果。
(四)模式识别
数学应用题存在模型,这是数学教师在教学实践中总结出来的经验。在问题解决中,解题者调用头脑中的模型来解决当前问题,就是模式识别。
施铁如通过对初一年级两组学生的对比实验发现:能否识别应用题的类型在很大程度上决定着能否迅速、准确地解答问题;要正确识别应用题的类型,需要从具体的语义情境中分出确定的、一般的结构关系,这既依赖于对当前题目信息的加工,也依赖于对记忆中贮存的有关信息的搜寻;识别题目类型的训练有利于形成解题技能,而这种训练应该围绕模型选择多种多样的变式习题来进行。
王亚同等将例子的概括化程度称为图式化程度。图式化本质上就是一种模式化。他们研究发现,利用由结构类似性形成的代數图式可以比较容易地解决目标问题。
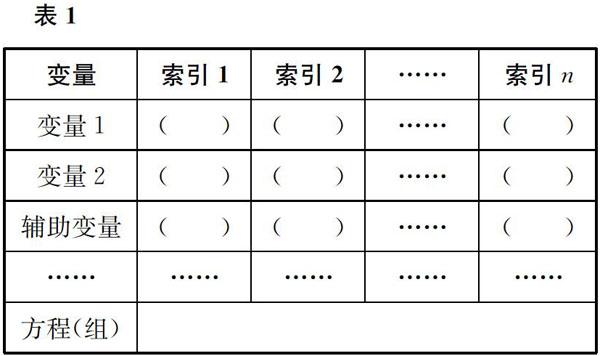
陆昌勤等做了对比实验:在实验班采用解答代数应用题的认知过程模式教学——对每道题目,学生都要填写表1;在控制班按照传统方式教学。结果表明,实验班学生解题正确率非常显著地高于控制班,因为实验班学生的头脑中形成了解决问题的模式,有优良的认知结构。
(五)元认知及非智力因素
许多研究证实,元认知及非智力因素对问题解决有显著影响。童世斌等采用对比实验,对实验班进行两个阶段的训练。第一阶段,训练掌握元认知知识,即解决问题的有效思维策略。训练内容包括:准确理解题意,理清复杂的数量关系,寻找隐含的数量关系,总结解题思路。第二阶段,训练元认知监控。利用“元认知监控自我提问单”训练学生通过自我监视和控制来确保自己在问题解决过程中运用所学的策略性知识。结果表明:学生的思维策略训练效果显著,中等生、差生的效果尤为显著;在思维策略训练的基础上加上元认知监控训练,能够更有效地提升解答数学应用题思维训练的效果。
由于数学应用题的篇幅长、背景陌生,不少学生对数学应用题有着与生俱来的畏惧感。数学焦虑是情感,也是认知方面对数学的恐惧,指学生在数学学习过程中由于过度的担心和忧虑而引起的一系列生理上和心理上的消极状态。宋广文等通过对初中学生进行测量研究,发现数学焦虑对解答应用题的成绩具有一定的负向作用。
二、对中学数学教学的启示
上述应用题解决的一些心理学研究,可以给我们一些有益的启示,从而提出如下几点中学数学应用题教学策略。
(一)丰富领域知识,形成扎实基础
掌握基础知识,形成基本技能,是教学三维目标中的第一维,也是学生发展数学核心素养的基础。事实上,上述关于领域知识的丰富的心理学研究,本质上就指向“双基”的扎实性。基础知识的厚实、基本技能的娴熟,不仅对解决应用题有举足轻重的作用,而且对解决所有的数学问题都至关重要,是数学学习质量高低的一个显性指标。
在应用题教学中,要丰富学生的数学领域知识,可考虑如下两点:
首先,帮助学生在长时记忆中贮存必需的公式、定理和法则。解决应用问题会用到大量的数学公式,如速度公式、浓度公式、复利公式等。不仅如此,解决应用题还会用到一些跨领域的知识。一是数学学科内部的跨领域。比如,许多应用题都与距离有关,而距离是线段的长度,因而,大多数求距离的应用题,可能会与平面几何、三角函数、解析几何的一些公式、定理有关系。二是跨学科领域。比如,解决数学应用问题可能会用到物理、化学、生物等学科的相关公式、法则。因此,记忆重要的知识是解答应用题的必要条件,教师应该将知识分门别类,帮助学生形成知识体系,有序贮存知识。
其次,帮助学生总结题目类型,形成解题模式。如前文所述,心理学的相关研究表明,对模式进行有效的识别是解决应用问题的关键。波利亚也提倡解题模式的训练,他提出的笛卡儿模式、双轨迹模式等就是数学解题模式的典范。事实上,许多学生对应用题的错误解答,或者是因为无法识别题目类型,或者是因为错误识别题目类型。因此,教师要帮助学生养成辨析问题类型的习惯,提升识别模式的能力。当然,这样做的前提是学生头脑中具备相关的模式。对此,可以采用“解题总结、分门别类、提炼方法、形成模式”的路径。
(二)加强审题训练,提升表征水平
审题与问题表征直接相关,审题的质量影响问题表征的质量。因此,加强对学生审题的训练十分必要。
审题教学可以分为以下几步:分层理解,分类整理,分步反推。首先,引导学生采用“首次读题区分策略”通读题目,对题目信息中的问题背景、基本元素的数量或位置关系、解题目标进行分层理解。第一遍通读,主要了解问题背景、明确解题目标。其次,引导学生采用“‘问题—引导策略”“以特征为基础策略”等进行精读,在问题的引导下借助图形或表格清晰地表述关键信息,并将文字语言进行初步的数学表征。第二遍精读,关注与解题相关的数量或位置关系。最后,引导学生分步反推,寻找已知条件与解题目标之间的联系、隐含信息以及相关知识。
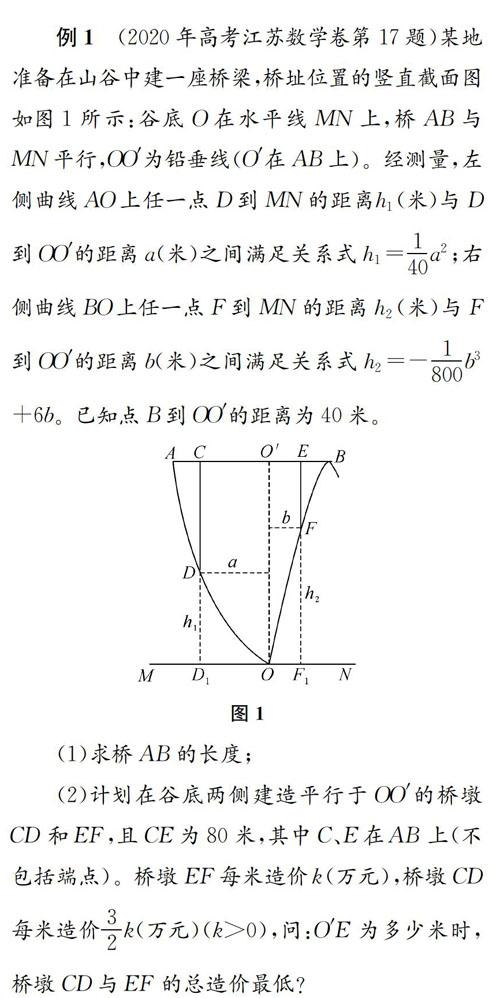
例1(2020年高考江苏数学卷第17题)某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图1所示:谷底O在水平线MN上,桥AB与MN平行,OO′为铅垂线(O′在AB上)。经测量,左侧曲线AO上任一点D到MN的距离h1(米)与D到OO′的距离a(米)之间满足关系式h1=140a2;右侧曲线BO上任一点F到MN的距离h2(米)与F到OO′的距离b(米)之间满足关系式h2=-1800b3+6b。已知点B到OO′的距离为40米。
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于OO′的桥墩CD和EF,且CE为80米,其中C、E在AB上(不包括端点)。桥墩EF每米造价k(万元),桥墩CD每米造价32k(万元)(k>0),问:O′E为多少米时,桥墩CD与EF的总造价最低?
1.分层理解。
通读题目后,可将题目的文字信息初步分为3个层次。第一层次:问题背景——在山谷中建桥梁;第二层次:与桥梁相关的元素的数量与位置关系;第三层次:解题目标——桥的长度、桥墩总造价何时最低。
2.分类整理。
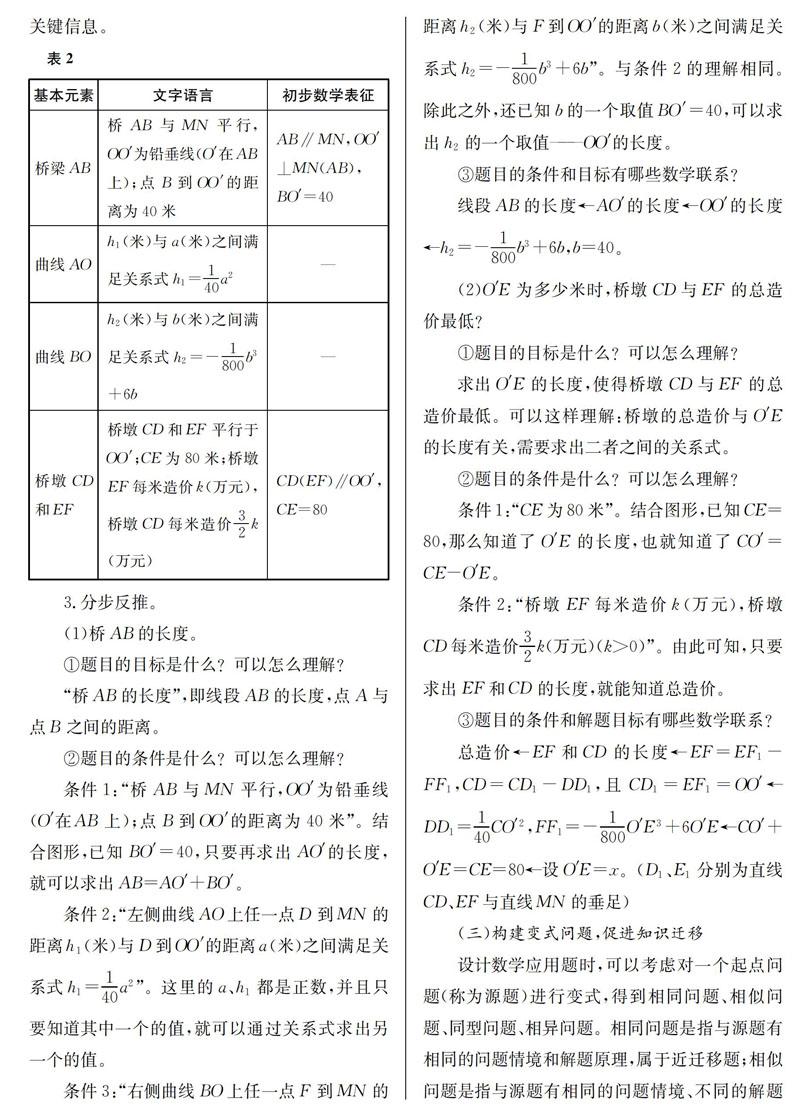
了解问题背景和解题目标后,采用“问题—引导”策略精读基本元素的数量与位置关系信息。教师可以引导学生借助表格对相关信息集中整理(得到下页表2),使学生比较清晰地抓住关键信息。
3.分步反推。
(1)桥AB的长度。
①题目的目标是什么?可以怎么理解?
“桥AB的长度”,即线段AB的长度,点A与点B之间的距离。
②题目的条件是什么?可以怎么理解?
条件1:“桥AB与MN平行,OO′为铅垂线(O′在AB上);点B到OO′的距离为40米”。结合图形,已知BO′=40,只要再求出AO′的长度,就可以求出AB=AO′+BO′。
条件2:“左侧曲线AO上任一点D到MN的距离h1(米)与D到OO′的距离a(米)之间满足关系式h1=140a2”。这里的a、h1都是正数,并且只要知道其中一个的值,就可以通过关系式求出另一个的值。
条件3:“右侧曲线BO上任一点F到MN的距离h2(米)与F到OO′的距离b(米)之间满足关系式h2=-1800b3+6b”。与条件2的理解相同。除此之外,还已知b的一个取值BO′=40,可以求出h2的一个取值——OO′的长度。
③题目的条件和目标有哪些数学联系?
线段AB的长度←AO′的长度←OO′的长度←h2=-1800b3+6b,b=40。
(2)O′E为多少米时,桥墩CD与EF的总造价最低?
①题目的目标是什么?可以怎么理解?
求出O′E的长度,使得桥墩CD与EF的总造价最低。可以这样理解:桥墩的总造价与O′E的长度有关,需要求出二者之间的关系式。
②題目的条件是什么?可以怎么理解?
条件1:“CE为80米”。结合图形,已知CE=80,那么知道了O′E的长度,也就知道了CO′=CE-O′E。
条件2:“桥墩EF每米造价k(万元),桥墩CD每米造价32k(万元)(k>0)”。由此可知,只要求出EF和CD的长度,就能知道总造价。
③题目的条件和解题目标有哪些数学联系?
总造价←EF和CD的长度←EF=EF1-FF1,CD=CD1-DD1,且CD1=EF1=OO′←DD1=140CO′2,FF1=-1800O′E3+6O′E←CO′+O′E=CE=80←设O′E=x。(D1、E1分别为直线CD、EF与直线MN的垂足)
(三)构建变式问题,促进知识迁移
设计数学应用题时,可以考虑对一个起点问题(称为源题)进行变式,得到相同问题、相似问题、同型问题、相异问题。相同问题是指与源题有相同的问题情境和解题原理,属于近迁移题;相似问题是指与源题有相同的问题情境、不同的解题原理,属于中迁移题;同型问题是指与源题有不同的问题情境、相同的解题原理,属于中迁移题;相异问题是指与源题有不同的问题情境和解题原理,属于远迁移题。
对于相同问题,通过教师对例题的讲解,学生容易实现迁移,因为这是一种模仿性解题行为。对于相似问题,由于问题情境不变而解题原理变了,学生容易受到情境的影响产生负迁移,即还是企图利用原来的原理解决,因此,解决起来存在一定的困难。对于同型问题,由于问题情境变了而解题原理不变,教师应当注意引导学生从不同的情境中概括出相同的原理,这样不仅可以提高学生解决问题的迁移能力,还能发展他们的数学抽象素养。
例如,有些代数应用题可以使用“单价×数量=总价”“速度×时间=路程”“工作效率×工作时间=工作量”等数量关系来解决。如果教师将这一系列同型问题的解答过程放在一起,引导学生归纳出一个更具有概括性的数量关系,即“单位量×单位时间=总量”,就达到了同型问题的训练目的。
例2(源题)客车从甲地到乙地需要20小时,货车从乙地到甲地需要30小时,现在两车分别从甲乙两地同时相向开出,多少小时后两车相遇?120x+130x=1
(相同问题)汤姆从自己家开车到比尔家需要4小时,比尔从自己家开车到汤姆家需要3小时。如果他们同时从自己家开车向对方家驶去,要多久才能见面?14x+13x=1
(同型问题)①将1400元奖学金按照两种奖项奖励给22名学生,其中一等奖每人200元,二等奖每人50元,则获得一等奖的学生有多少人?[200x+50(22-x)=1400]
②买了共138米的两种布料,花了540元,其中蓝布料每米3元,黑布料每米5元,则两种布料各买了多少米?[3x+5(138-x)=540]
(相似问题)两辆汽车从相距84 km的两地同时出发相向而行,甲车的速度比乙车的速度快20 km/h,半小时后两车相遇,则两车的速度各是多少?12x+12(x+20)=84
以上的源题、相同问题、同型问题、相似问题可以让学生依次解答。学生全部解决后,教师可以同时呈现问题以及对应的方程,引导学生归纳出更一般的数量关系——“部分1+部分2=总体”。这样,学生即使遇到背景陌生的应用题,只要抓住这个数量关系,去题目中寻找信息,将部分与整体分别用代数式表示出来,就可以解决一大类应用题。
(四)设计自我提问单,提升监控水平
心理学研究表明,优秀生在解决应用题时能有效地监控自己的认知加工过程,而中等生、差生则缺少有效的自我监控,但经过一段时间的元认知训练后,中等生、差生解题效果有显著的提升。因此,在教学中,教师应该有意识地对学生进行元认知训练。
元认知训练可以分为内隐训练和外显训练。内隐训练主要是通过在教学过程中示范性地解释解题所用的程序性知识和策略性知识,让学生体会元认知策略的有效性;外显训练可以通过制作一个与课堂传授的元认知策略相一致的“元认知监控自我提问单”,要求学生在解题时回答相应的问题,达到监控自己认知加工过程的目的。当学生对这一系列的元认知策略应用自如时,说明他们已将元认知知识内化,可以不再要求他们在解题时填写提问单。
“元认知监控自我提问单”的设计,可以以波利亚的“怎样解题表”为基础,根据不同时间段、不同知识点进行相应的修改。例如,上述例1审题教学中的“分步反推”环节所提的问题即是“元认知监控自我提问单”的部分问题。
整体地看,“元认知监控自我提问单”可以分为以下三个部分:
(1)审题环节:①问题的背景是什么?②解题目标是什么,应当怎么理解?③已知条件是什么,可以怎么理解?④能画一个表或者一张图,将题目中的关键信息表示清楚吗?
(2)拟定、执行方案环节:①已知条件和解题目标之间有哪些数学联系?②如果看不出有哪些联系,再观察解题目标,能否想出一道自己熟悉的具有相同或相似解题目标的问题?③如果感觉数据太抽象,能否用具体的数据替换抽象的数据寻找解题思路?
(3)回顾反思环节:①能否判断每个步骤都是正确的?②问题的答案是否有现实背景?③回顾解题过程,遇到了什么困难?有哪些收获?④解题方法是否具有一般性?是否能在其他题目的解答中利用这个方法或思路?
*本文系喻平教授团队的“数学学习心理学研究及其教学启示”(中学)系列文章之七。
参考文献:
[1] 胥兴春,刘电芝.问题表征方式与数学问题解决的研究[J].心理科学进展,2002(3).
[2] 傅小兰,何海东.问题表征过程的一项研究[J].心理学报,1995(2).
[3] Mayer R., Hegarty M., Monk C.Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers[J].Journal of Educational Psychology,1995(1).
[4] 冯虹,阴国恩,安蓉.数学成绩与代数应用题分类结果的相关研究[J].心理与行为研究,2007(2).
[5] 姜子云,邓铸.问题表征过程中信息提取的实验研究[J].心理科学,2008(3).
[6] 张维,蔡笑岳,曾苑霞.学科领域知识丰富性对中学代数问题表征层次的影响[J].心理科学,2011(2).
[7] Zhang J.The Nature of External Representation in Problem Solving[J].Cognitive Science,1997(2).
[8] 邢强,单永明.数学应用题外部表征的影响因素及启发[J].数学教育学报,2012(5).
[9] 赵继源.“冷轧机”问题为什么是高考应用题中的难题——基于实证研究的一些發现[J].数学教育学报,2007(3).
[10] 章巍.代数应用问题的文字表述对解题影响的研究[J].数学教育学报,2014(2).
[11] John Sweller.Some cognitive processes and their consequences for the organization and presentation of information[J].Australian Journal of Psychology, 1993(1).
[12] 冯虹,阴国恩,陈士俊.代数应用题解题过程的眼动研究[J].心理科学,2009(5).
[13] Littlefield J., Riser J.J.Finding the Critical Facts: Childrens Visual Scan Patterns when Solving StoryProblems that Contain Irrelevant Information[J].Journal of Educational Psychology,2005(2).
[14] 岳宝霞,苏颖,冯虹.题目难度和冗余信息对代数应用题信息区分策略影响的实验研究[J].数学教育学报,2013(6).
[15] 张锦坤,连榕.初二学生解几何应用题策略类型的研究[J].心理科学,2007(2).
[16] 施铁如.解代数应用题的认知模式[J].心理学报,1985(3).
[17] 王亚同,唐耿新.图式化程度对解决代数文字题的影响[J].应用心理学,2003(2).
[18] 陆昌勤,周谦.问题解决的实验性研究——解代数应用题的认知结构[J].心理科学,1998(3).
[19] 童世斌,张庆林.元认知训练对提高中学生解答数学应用题能力的实验研究[J].心理发展与教育,2004(2).
[20] 宋广文,李守龙.数学焦虑对初中生数学应用题成绩的影响[J].心理学探新,2009(1).
