数学实验让小数概念意义的建构看得见

2020-10-30席爱勇吴玉国

教学与管理(小学版) 2020年2期

席爱勇吴玉国

数学实验小数概念意义建构的工具技术支撑借此此以“看见”小数多重意义的多维模型建构，有效突破小数概念意义建构的思维藩篱，帮助教师优化教学资源，灵活组织教学方式，走向深度理解的数学教学实践。

一、数学实验让小数概念意义建构的多维模型看得见

小数的概念有两个来源：是源于现实世界数量的表达;二是源于数学自身数系的发展。小数可以看成是按照十进制等分的结果：因为十进制，它可以和整数建立关联;因为等分，它又可以和分数建立关联。因此，小数概念意义建构的数学实验，既可以从生活切入，也可以从整数切入，还可以从分数切人。

1.从生活切入，开展小数生活意义建构的数学实验

在小数的初步认识阶段，目前的小学数学教材都选择紧密联系学生生活实际的学习材料。因此，我们可以从生活实际切入，开展小数概念建构的数学实验。例如我们可以开展“生活中的小数探寻实验，首先开展实验调查，走进超市、菜市场、社区、医院等场所，调查用小数表示的商品价格、物品重量及各类人员的身高体重等;然后开展实验讨论，说说调查出来的小数各表示什么意思，对小数尝试进行解释说明;再次进行实验验证，请教老师、家长和专业人士，看看对小数的解释是否正确;最后回归生活实际，尝试进行实践应用。

2.从整数切入，开展小数度量意义建构的数学实验

小数和整数都是建立在十进制框架下的数。因此，小数也可以通过数学实验来建构其度量意义。首先，我们可以通过数小正防形或计数器模型的数学实验，让学生感受到10个一是1个十，10个十是1个百……识到满十进一的十进制本质;然后，我们再倒过来，把1个百平均分成10份，每份就是1个十;把1个十平均分成10份，每份就是1个一;把1个一平均分成10份，每份怎么表示呢？从而引入一位小数，每份就是0.1，10份就是10个0.1，即1。这样就自然建构了一位小数的度量意义，融通了小数和整数之间的内在关联。用胴样的数学实验方法可以建构两位小数、三位小数的度量意义，融通它们之间的内在关联。

3.从分数切入，开展小数等分意义建构的数学实验

分数的本质是把“单位1”平均分成若干份，表示这样一份或几份的数。十进分数是分母是10、100、1000……特殊分数，而小数可以看作是十进分数的改写形式。因此，我们可以从分数切人，开展基于小数等分意义的数学实验。首先借助实物米尺或线段图形等均分认识一般分数，如号、一….，指出去还可以写成0.1，这样就从十进分数自然引人小数，接着让学生借助实物或图形涂出，分别将这些分数改写成对应小数，建构一位小数和分母是10的分数的一对应关系。用胴样的方法，可以建构两位小数和分母是100的分数的一对应关系……通过开展十进分数的等分实验来认识对应小数的等分意义，实现小数等分意义的建构。

二、数学实验让小数概念意义建构的思维突破看得见

数学实验，让学生在“做”中享受完整的数学学习，给学生数学思维提供工具技术支撑，能够有效突破小数概念意义建构的思维藩篱，不断提升数学思维品质，让学生思维更清晰、全面和深刻州。

1.让思维更清晰

在小数的意义建构中，很多学生因2个0.1是0.2、3个0.1是0.3……个0.1是0.9，思维定势地认为10个0.1是0.10而不是1。在这个思维节点，可以通过数学实验，把一个正方形看作1，平均分成10份，涂1份是0.1，涂2份就是2个0.1，即0.2……涂9份就是9个0.1，即0.9，涂10份就是10个0.1，正好把一个正方形全部涂满，应该是多少呢？学生自然地看出是1，而不是0.10，并体悟到一位小数和整数一样也是满十进一。

2.让思维更全面

在小数的意义建构中，一些学生会认为一位小数就是零点几。为了突破学生数学思维的不全面，让学生认识到一位小数是几点几，可以联系生活实际开展系列数学实验。如开展探究性数学实验：1角是。元，用小数标就是0.1元;2角是台元，用小数表示就是0.2元……元1角怎样用分数和小数表示？学生联系生活实际，通过探究性数学实验，得出1元1角是会元，用小数表示就是1.1元。进一步圳导学生探究发现：1.1也是一位小数，不是零点几，而是几点几。这样，自然就会扭转学生“一位小数就是零点几”的不全面认识。

3.让思维更深刻

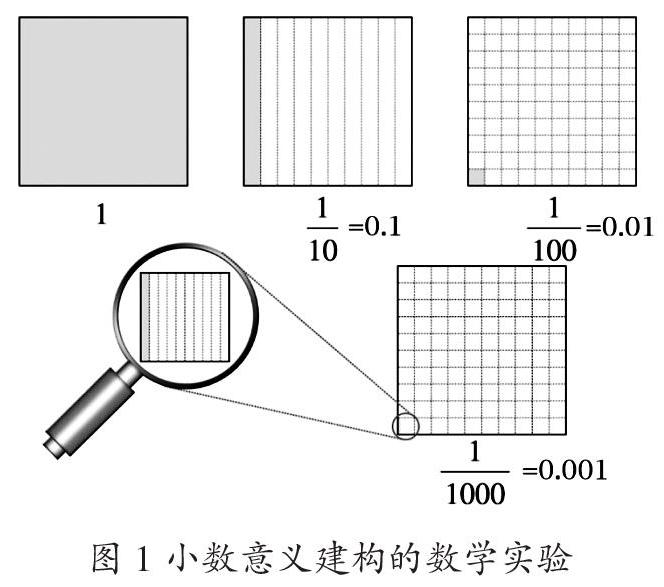
在小数的意义建构中，帮助学生理解小数相邻两个计数单位之间的进率是十，也是一个教学重难点，突破这个教学重难点同样可以通过数学实验来实现。如让学生通过正方形模型分一分、涂一涂等操作性数学实验（图1），认识到1里面有10个0.1，0.1里面有10个0.01，0.01里面有10个0.001……在此基础上进行直观想象，总结归纳小数和整数一样，相邻两个计数单位之间的进率是十。

当然，教师也可以利用米尺、数轴图等工具进行操作性数学实验，通过数一数、填一填等方式帮助学生理解小数和整数一样，相邻两个计数单位之间.的进率都是十，突破思维疑难点，使思维更深刻。

三、数学实验让小数概念意义建构的教学实践看得见

基于数学实验的课堂教学实践，让学生在做中思，在思中悟，经历连续关联、循环的序列推进，享受数学学习的完整過程。

1.连续：在数数中连续十进制概念

连续即教师要寻找与学生新知识学习相连的已有生活经验或知识经验基础，从这里延续，激发学生数学学习的积极心向，引导学生整体自然地进入数学学习状态。如引导学生通过数方块图或计数器实验，明白10个一是1个十、10个十是1个百……此基础。上总结十进制计数法，为学生进行小数的等分意义和数位意义建构一个大概念数系系统，以便实现数学知识原理、数学思维方法、数学思想价值等多方面迁移拓展。

2.关联：在十进制数系中关联小数

关联即教师要引导学生抓住数学知识的关键节点，迁移拓展关联新知，通过归纳类比等思维方式完成新知识的自我意义建构。如利用十进制计数法引导学生倒过来想：“把1个百平均分成10份，每份就是1个十;把1个十平均分成10份，每份就是1个一。同学们，你们有没有想过，如果把1再平均分成10份，每份会是多少呢？”一下子将学生的思维推向十进分数或一位小数的最近发展区，让学生自己摘“桃”，自我建构小数的等分意义和数位意义。学生通过十等分、百等分、千等分数学实验，自然就会发现分母是10、100、1000的分数都可以用小数来表示，进而发现只要是十进分数，都可以用小数表示。

3.循环：在多元表征中实现整数、十进分数和小数的统整

循环即在多元表征和实践应用中实现数学知识技能、方法策略和价值观念的循环上升，促进学生数：学素养的养成。笔者在教学小数的意义时，通过设计如下几个层级的数学实验，实现整数、十进分数和小数意义的统整。

1.自由表达，在实物图形、文字和符号表征对比中感悟小数的简约性。

（1）出示由一枚1元硬币和6枚1角硬币的图片：这是小明储蓄罐里倒出的钱，你能看出来有多少钱吗？（1元6角，或1.6元）用1.6元表示的同学是怎样想的？

（2）比较：1元6角和1.6元，你更喜欢哪种表示方法？为什么？

2.单位换算，在文字和符号表征的转换中统整十进分数和小数。

（1）在括号里填上合适的小数。

6毫米=（）厘米

6毫米=（）分米

6毫米=（）米

（2）讨论：都是6毫米，为什么后面填的数不一样？

3.对应填数，在数轴与符号对应表征中深刻理解小数进率。