基于PSO 优化极限学习机的机器人控制研究

杜玉香，赵月爱

（1.广州南洋理工职业学院 机电与汽车学院，广东 广州 510925；2.太原师范学院 计算机系，山西 晋中 030619）

机器人技术迅速发展，其应用场景更加精细化，功能性要求越来越高，控制精度和实时反馈等需求明显提升。随着模式识别技术发展与深度学习算法的日趋成熟，机器人控制迎来了新的发展机遇［1］，传统的被动接受指令，亦步亦趋的机器人控制模式正在被改变，半自动和全自动自主学习逐步嵌入到机器人控制系统中。当前，不论是在机器人应用环境感知方面，还是动作行为多样化及控制方法精细化等方面，都有了更先进的技术支持［2］，比如指令操作的多样加权融合能够让机器人实现更加复杂且精准的行为操作，灵敏感知周围环境，能够在复杂环境中实现功能应用等。

目前，关于机器人的控制研究较多，主要集中在前端的环境感知研究和后端的定位和控制算法策略研究，文献［3］结合视觉技术，采用卷积神经网络实现机器人的物体精确定位识别，识别准确度高；文献［4］采用借助极端学习机的代数矩阵求解方法，完成了并联机器人的运动控制。本文采用极限学习机算法来实现机器人的多样行为控制，并结合粒子群（Particle swarm optimization，PSO）算法来对极限学习机权重和阈值进行初值优化，有效提高极限学习机的控制效率。

1 机器人控制系统

1.1 机器人控制体系

机器人通过传感器获得环境特征，搭建环境模型，明确目标任务，生成行为控制指令，最后通过动作执行器执行行为指令。根据工作流程，可以简单将机器人功能模块划分为6个部分［5］，如图1所示。其中，传感器感知数据融合和运动规划及控制是机器人控制研究的重点内容，一般都需要算法来实现，前者需要算法对多传感器感知环境数据进行特征筛选、降维和融合等，后者需要通过算法来实现路径选择和精确控制。

1.2 机器人控制的主要行为

机器人根据感知的环境特征做出行为反馈，常见机器人反应式控制结构如图2所示。在机器人的精准控制中，是多个行为叠加求和的控制策略［6］，比如避障、姿态维持、趋向目标等行为。执行机构执行的命令通过多种行为加权后得到，而权重是与机器人环境紧密相关的，会随着环境的改变而发生变化，各种行为的权重值需要准确计算才能完成机器人的高效控制，从而保证机器人能够在复杂多变的环境中顺利运行。本文采用极限学习机来实现权重的计算。

2 PSO优化极限学习机的机器人控制

2.1 单隐层神经网络

设N个带标签的数据样本S={(xi,ti)|xi∈Rn,ti∈Rm,i=1,2,…,N}，其中 xi=[xi1,xi2,…,xin]T，ti=[ti1,ti2,…,tim]T。样本经过转换函数 g(⋅)，隐藏层节点为 N͂的神经网络训练［7］，得到输出结果为

其中：wi=[wi1,wi2,…,win]T和 βi=[βi1,βi2,…,βim]T分别表示与第i个节点相连的权重和阈值。

式（1）采用矩阵的方式可以写成

H和β相乘的具体计算方法为［8］

结合样本标签，找到合适的 ŵi，b̂i，β̂i值，满足式（4），获得稳定的网络结构模型。

将式（4）的求解方法转换得到［9］

为了求解‖Hβ-T‖的极小值，将神经网络结构中(wi,βi)的值表示为矩阵W，采用梯度下降方法求解

式中：η表示学习步长。采用这种方法求解时间加长。

2.2 极限学习机

通过梯度下降，权重和阈值在迭代中变化，而极限学习机在初始权重和阈值随机设定后，保持不变，按照此法，对式（4）进行优化［10］

当N͂=N时，采用通过常规数学方程获得wi，bi，βi的结果；若 N͂≪N ，则 Hβ=T 无法通过解常规方程的方法来求解［11］，因此需要寻找近似解 β̂i，b̂i，ŵi来满足式（7）。

根据最小范数二乘解定理，式（2）满足

H╀表示H的逆矩阵，求解方法为［12］

采用这种方法可以解决N͂≪N的问题，但必须满足g(x)是连续可微的。

2.3 PSO优化算法

将极限学习机的初始权重和阈值作为粒子群的粒子，设第i个粒子xi=(xi1,xi2,…,xiN)的飞行速度为vi=(vi1,vi2,…,viN)，以机器人趋向目标准确率作为适应度函数。分别求解各粒子适应度值，第i个粒子的适应度极大值为 pi=(pi1,pi2,…,piN)，群里所有粒子的极大值为 pg=(pg1,pg2,…,pgN)［13］。粒子速度更新方法为［14］

式中：c1和c2表示学习因子，一般情况取值c1=c2=2；ω表示上时间段的速度权重；r1,r2∈rand(0,1)；r为约束系数。

2.4 机器人控制流程

极限学习的权重和阈值是随机设定的，这样会增加算法时间，因此考虑将粒子群算法用于权重和阈值初值的优化，通过优化提高极限学习机的速度。

将障碍物坐标、目标坐标、动作行为等作为输入，将避开障的准确度和趋向目标的精度作为机器人控制的标准，通过极限学习机求解，得到相应行为动作的权值，最后通过加权求和获得动作结果。具体流程如图3所示［15］。

3 实例仿真

为了验证PSO优化极限学习机在机器人控制研究中的性能，采用Matlab进行实例仿真。仿真数据样本共计200个，1个样本数据主要包括地图栅格、障碍坐标、目标坐标、行为数据、路径数据。行为数据库主要包括9种行为，具体动作及编码详见表1。

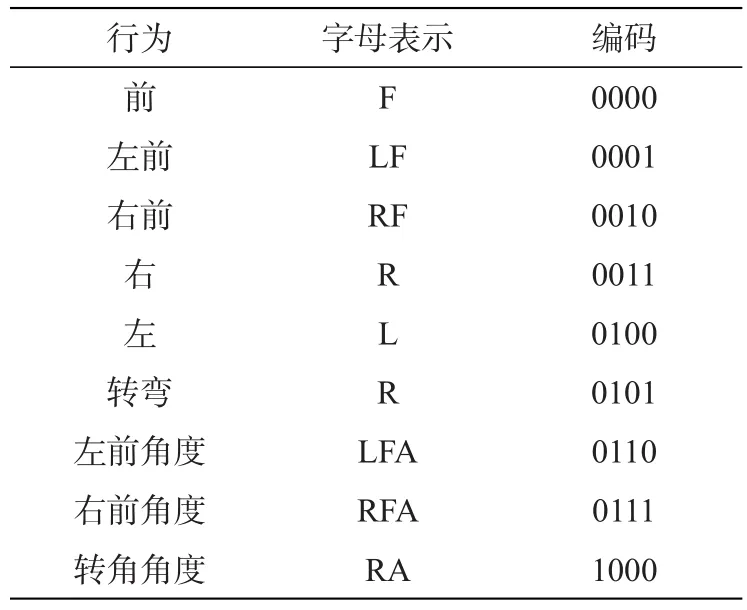
表1 机器人主要行为动作编码Tab.1 Code of main motions of robot

3.1 机器人控制路径仿真

根据样本中的障碍物坐标和目标坐标进行路径规划仿真，地图为200 cm×200 cm的正方形。选取一个样本的仿真结果如图4所示。机器人初始坐标为［-100，-100］，目标物坐标为［60，70］，障碍物点共计50个，机器人执行了左前、右转向，右前、左转向等行为操作，在二维平面中避开了所有障碍点，选择了合适路径到达了目标物坐标点。

3.2 PSO优化对机器人控制性能影响

选取极限学习机和经过PSO优化的极限学习机算法分别对趋向目标准确率和运算时间进行仿真。收敛时机器人位置距离目标坐标点1 cm范围内均表示目标趋向判定成功，否则运动控制判别失败。

考虑到极限学习机结构受隐藏层节点数的影响较大，差异化设置隐藏层节点数量，分别对不同隐藏层节点数的机器人运动控制的目标趋向准确率进行仿真，结果如图5所示。

经过PSO优化后的极限学习机在机器人控制方面目标趋向性能更优，最高准确率达到100%。在隐藏层节点数较小时，两者的趋向目标准确率相差不大，节点数增大时，两者差距拉大。当隐藏层节点数为35时，两者的趋向目标准确率不再变化。因此，对于本例实验仿真最优隐藏层节点数为35。

对两种算法的收敛时间进行仿真，比较不同隐藏层节点数下算法的收敛时间，结果如图6所示。当隐藏层节点数增多，两种算法的收敛时间均变长，但PSO极限学习机算法收敛时间明显低于极限学习机。这是因为神经网络结构增大，极限学习机需要消耗更多的时间计算权重和阈值参数，而PSO极限学习机算法因为对权重和阈值初值进行了优化，因此能够获得更优的收敛时间。

3.3 速度权重对控制算法准确率影响

速度权重ω值影响PSO的收敛速度和全局寻优性能。为了进一步验证本文算法对机器人控制的性能，选取不同的ω，计算趋向目标准确率和收敛时间。仿真结果如表2所示。ω增大，趋向目标准确率提升，但收敛时间也随之增加。这是因为ω增大更便于获得全局最优值，能够得到准确的目标坐标。综合对比，速度权重ω=1.2最适合于本文数据样本。

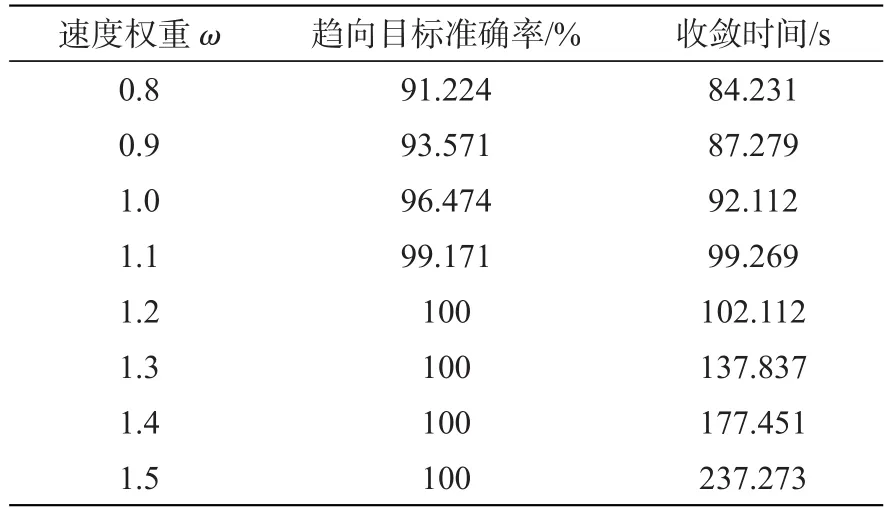
表2 不同速度权重的控制性能Tab.2 Control performance at different speed weights

4 结 论

本文提出了一种基于PSO优化极限学习机的机器人控制方法。该方法在隐藏层节点数达到一定数量时，能够实现二维地图的完美避障，并获得较高的趋向目标准确度。实验结果表明，通过合理设置PSO的速度权重，平衡趋向目标准确度可以达到100%，且收敛时间仍在可接受范围，从而有效提高了对机器人控制的性能。后续研究将进一步优化PSO算法学习因子等参数，以提高PSO优化极限学习机在机器人控制中的适应度。