飞翼无人机机动飞行非线性反步控制律设计

杨雷恒，李继广，杨璐，岳源

(1.西安航空职业技术学院 通用航空学院， 西安 710089)

(2.西安航空学院 通用航空工程技术中心， 西安 710077)

(3.中国民用航空飞行学院 航空工程学院， 广汉 618307)

0 引 言

飞翼无人机由于具有良好的隐身性能、较大的升阻比等优点受到了各国的普遍重视，得到了较快的发展。虽然飞翼布局的优势突出，但其特殊的构型也为控制律设计带来了一系列的困难：

(1) 垂尾的缺失使得航向稳定性弱，且存在更大的耦合和非线性特性[1-2]；

(2) 控制效率低下使得机动飞行时非线性、迟滞效应、不确定扰动等的影响更加突出[3-4]；

(3) 机动飞行的飞行状态快速改变使得经典控制理论所要求的平衡点并不存在，这也使得经典控制方法失去了理论基础[5-6]。

针对飞翼无人机机动飞行面临的实际问题，各国研究者提出了不同的解决方法。L.Sonneveldt等[6]、S.Sieberling等[7]、W.MacKunis等[8]从不同的理论角度出发研究了无人机的非线性控制问题。这些研究结果对解决飞翼无人机机动飞行控制律设计是有利的，但是这些方法也存在着设计过程复杂、对系统模型精确高度依赖、鲁棒性无法保证等缺点。为了解决系统鲁棒性能设计问题，E.N.Johnson等[9]、Xu Bin等[10]做了专门的研究设计，并在X-35和F-18的模型机上进行了仿真验证。这些方法虽然提高了系统的鲁棒性，但是设计过程要求系统不确定性是有界且已知的。

目前，已经发展了很多非线性控制律设计方法。在众多非线性控制方法中，反步(Backstepping)控制方法因其具有处理非线性系统控制的能力，在飞翼无人机控制系统设计上表现出明显的优势并得到了广泛的重视。然而，传统Backstepping方法同样具有鲁棒性弱、设计过程复杂等不足。为了提高系统的鲁棒性，研究者提出了改进方法[11-12]。但是，这些方法在提高系统鲁棒性的同时，也带来了奇异值计算、保守性等问题。

本文针对奇异值计算、保守性问题，提出一种改进的Backstepping方法，运用该方法进行控制器设计，并对控制器进行仿真验证。

1 系统建模

被控飞翼无人机示意图如图1所示，可以看出：该无人机是典型的飞翼布局，控制舵面主要包括升降副翼，两边舵面联动相当于升降舵，两边舵面差动相当于副翼；同时，该无人机具有阻力式方向舵。

图1 无人机示意图

为了表述方便，将无人机的姿态方程表述为如下形式：

(1)

式中：ω=[p,q,r]T；MA为无人机运动与空气的相互作用而产生的气动力矩；MT为发动机矢量喷口偏转而产生的矢量力矩；I和S(ω)分别为惯性矩阵和ω的反对称矩阵。

发动机的矢量力矩，一般用发动机的油门开度δth、发动机喷口矢量角纵向偏转角度δp和横向偏转角度δy进行调节。当发动机推力作用点到质心沿机体轴的距离为xT,推力大小表示为飞行状态和油门开度的状态函数T(x,δth)时，则发动机的矢量力矩为

(2)

无人机的姿态角运动方程为

(3)

式(1)所确定的飞翼无人机姿态方程和由式(3)确定的内环补偿控制律所组成的系统，可以表示成如下仿射非线性模型的形式：

(4)

(5)

式中：x1=[φθψ]；x2=[pqr]。

式(4)～式(5)的具体表达形式参见参考文献[2-3]。

为保证控制器的鲁棒性，将模型表示为包含有不确定性的摄动模型：

f1(x1)=f10(x1)+Δf1(x1)

(6)

b1(x1,x2)=b10(x1,x2)+Δb1(x1,x2)

(7)

b2=b20+Δb2

(8)

f2(x1,x2)=f20(x1,x2)+Δf2(x1,x2)

(9)

式中：f10(x1)、b10(x1,x2)、f20(x1,x2)、b20为系统的标称参数，其余为系统的不确定项。

2 鲁棒控制器设计

2.1 姿态角控制器设计

鲁棒自适应控制器设计的目的是在各种不确定性有界扰动的情况下，使得飞翼无人机系统的飞行状态收敛到任一指定无穷小的邻域内。令系统的误差量z1,z2∈R3为

(10)

式中：x1d,x2d为期望的系统状态轨迹。

由式(4)～式(5)可得误差状态的动态方程为

(11)

(12)

对于式(7)所确定的系统，其摄动模型可以表示为

Δb1(x1,x2)x2

(13)

令： Δ1=Δf1(x1)+Δb1(x1,x2)x2,

则：

(14)

式中：Δ1是系统的不确定项，即需要引入不确定函数进行补偿的各种不确定因素。

就实际系统而言，其不确定性是有界的，则存在一未知的正实数ρ1使得下式成立：

‖Δ1‖≤ρ1δ1(x1,x2)

(15)

式中：δ1(x1,x2)为已知的非负光滑函数。

将x2作为式(12)系统的虚拟控制量，则存在一个理想的虚拟控制量：

(16)

选取虚拟控制量为

(17)

式中：η1为需要设计的鲁棒函数系数，其作用是抵消各种不确定性因素Δ1的影响。

(18)

对式(18)求导可得：

(19)

根据文献[12-13],选择自适应调解律：

(20)

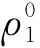
鲁棒函数系数η1和函数l1为

(21)

式中：ε1>0是需要的设计参数。

因为：

所以：

(22)

根据Lyapunov稳定性定理可知，该系统是稳定的。

2.2 角速率控制器设计与稳定性分析

由文献[12,13]可知，飞翼无人机姿态角控制器存在一个理想的控制输入：

(23)

使得式(24)成立。

(24)

式中：k2,k为要设计的大于零的参数。

(25)

对于研究对象来说，存在一个未知的正实数ρ2，使得:

‖Δ2‖≤ρ2δ2(x1,x2)

(26)

式中：δ2(x1,x2)为已知的非负光滑函数。

选取控制量：

(27)

式中：η2为期望提高系统鲁棒性而引入的鲁棒控制函数。

将式(27)带入式(24)可得：

b2(η2-Δ2)

(28)

选取Lyapunov函数：

(29)

对式(29)求导可得：

(30)

选择鲁棒函数和自适应调解律为

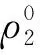
(31)

式中：

因此，系统是稳定的。

通过以上证明过程，有以下定理。

定理：对于由式(4)和式(5)所确定的系统，采用式(16)和式(27)所确定的虚拟控制量和控制量、以及自适应参数调解律，则系统的跟踪误差z1、z2参数估计误差有界，且以指数形式收敛于系统原点的一个邻域：

(32)

从以上定理可知，对于由式(4)和式(5)所确定的系统，通过调节k1、k2、σ1、σ2、r1、r2的值可以调节系统的收敛速度和收敛域。

3 仿真验证

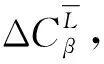
表1 偏移幅度表

为了更好地对比说明，本文采用动态逆设计方法和传统Backstepping方法进行仿真对比。其中，文献[7]提出的增量动态逆鲁棒设计方法(简称方法1)和文献[11]提出的一种滑模控制技术和Backstepping控制技术结合的无人机鲁棒非线性控制器(简称方法2)作为本文仿真的对照组。

滚转角通道响应如图2所示，曲线误差如图3所示，可以看出：三种方法具有不同程度的超调和稳态误差，但本文方法超调量更小，且没有稳态误差。但是，在方波信号的下降段，本文方法出现比较大的尖峰误差。

图2 滚转角通道方波响应

图3 滚转角通道方波响应误差

迎角通道正弦响应如图4所示，可以看出：本文提出方法具有更小的跟踪误差，而对照组方法具有相似的控制效果。

图4 迎角通道正弦响应

综上所述，本文方法在方波响应上升段和下降段的响应速度不如方法1和方法2，这也是图3中出现较大尖峰误差的原因。综合来看，本文所提出的设计方法具有较大的优势。

4 结 论

(1) 本文提出的改进Backstepping方法突破了现有非线性鲁棒设计方法对系统不确定性范数上界已知要求的限制，并充分利用系统已知的信息提高系统的性能。

(2) 该方法解决了鲁棒自适应函数设计过程中的奇异值计算问题和系统的保守性问题，具有较强的鲁棒性，和现有的方法相比具有一定的优势。