槟榔生物量预测模型建立与应用
2020-10-29陈才志周小霞王锋堂李培征陈奇李晗张瀚纠凤凤杨福孙
陈才志 周小霞 王锋堂 李培征 陈奇 李晗 张瀚 纠凤凤 杨福孙
摘 要:以海南本地種槟榔植株为材料,测量槟榔叶长(leaf length, LL)、叶宽(leaf width, LW)、叶片数(leaf number, LN)、花苞数(bud number, BN)、节数(node number, NN)、茎粗(stem diameter, SD)、株高(plant height, PH)、茎高(stem height, SH)和节间长度(internode length, IL)等可简单测量的特征指标,通过建立估测模型预测槟榔植株单片叶片干物质量(leaf dry weight, LDW)、茎杆干物质量(stem dry weight, SDW)及地上部分干物质量(aboveground dry weight, ADW)。结果表明:通过模型拟合和择优得到槟榔茎杆干物质量的估测模型为:SDW=0.2518 SD0+ 0.0423 PH23.8883,槟榔茎杆干物质积累量主要受株高(PH)、0 m茎粗(SD0)的综合影响,决定系数R2=0.7157,样本株数为36株,另外18株进行外部验证,相关系数r=0.9165;槟榔单片叶片干物质量的估测模为:LDW=3.9726 LL+2.8402 LW297.6869,槟榔单片叶干物质积累量主要受叶长(LL)、叶宽(LW)的综合影响,决定系数R2=0.6054,样本叶片数量为177片,另外88片进行外部验证,相关系数r=0.7528;槟榔地上部分干物质量的估测模型为:ADW=0.3283 SD0 + 0.0415 PH 23.7333,槟榔地上部分干物质积累量主要受0 m茎粗(SD0)、株高(PH)的综合影响,决定系数R2=0.6932,样本株数为36株,另外18株进行外部验证,相关系数r=0.9028。通过大量数据的观测分析,建立的槟榔生物量预测经验模型,可以将其作为最优生物量预测模型用于槟榔地上部分生物量的估算,具有一定应用价值。
关键词:槟榔;生物量;预测模型;养分吸收规律
中图分类号:S792.91 文献标识码:A
Abstract: In this paper, the plants of Hainan native betel nut species were used as the materials to measure the leaf length (LL), leaf width (LW), number of leaves (LN), number of flower buds (BN), node number (NN),stem diameter (SD), plant height (PH), stem height (SH) and internode length (IL). To predict the dry weight of single leaf (LDW), dry weight of the stem (SDW) and total dry weight in the aboveground part (ADW). The results showed that the estimated model for the dry weight of betel nut stems by model fitting and selection was SDW=0.2518S D0+0.0423 PH23.8883, the dry matter accumulation of betel nut stems was mainly affected by the plant height (PH) and 0 m stem diameter (SD0), the coefficient of determination R2 was 0.7157, the number of samples was 36, and another 18 were used as the external verification with a correlation coefficient r 0.9165. The model for estimating the dry weight of the leaves was LDW=3.9726 LL+2.8402 LW297.6869, the dry matter accumulation of the leaves was mainly affected by the combined effects of LL and LW, the coefficient of determination R2 was 0.6054, the number of sample leaves was 177, and another 88 were used as the external verification with a correlation coefficient r 0.7528. The model for estimating the total dry weight of the aboveground part was ADW=0.3283 SD0+0.0415 PH23.7333, the total dry weight in the aboveground part was mainly affected by SD0 and PH, the coefficient of determination R2 was 0.6932, the number of samples was 36, and another 18 were used as the external verification with a correlation coefficient r 0.9028. Based on the observation and analysis of a large number of data, the empirical model of betel nut biomass prediction was established in this paper, which could be used as the optimal biomass prediction model to estimate the biomass of betel nut.
Keywords: Areca catechu L.; biomass; prediction model; nutrient absorption
DOI: 10.3969/j.issn.1000-2561.2020.09.009
生物量作为植株群落最重要的数量特征之一,是直接反映植株生产力大小的重要指标[1]。生物量在狭义上指的是在给定时间单位面积内存在的有机物质总量,也就是植物干物質总量。林木生物量在各器官中的分配格局可以反映其适应性策略[2],植株在生长发育过程中,往往通过改变自身资源配置来提高适合度,以适应环境变化[3-4]。林木生物量包括地上生物量和地下生物量,其中茎、叶是植株地上主要组成部分,茎不仅起到机械支撑作用,而且具有输送水分以及运输养分的功能,叶片进行光合作用是积累植物生物量的主要来源[5]。茎、叶资源的配比,对植物的生长和繁殖有着直接的影响,是植物适应外界环境的综合结果[6]。目前,估算林木生物量的研究方法主要有两种方法:传统直接测量法和现代生物量间接估算法[7],传统方法主要包括相对生长模型法、皆伐法、标准木法等[8-9]。现代生物量间接估算法包括光学遥感估算法、雷达数据估测生物量[10]等。传统的直接测量法具有测量精度高的优点。因此,本研究依旧采用传统方法对槟榔植株茎、叶地上部分生物量进行模型预测,为简单、准确、快速、非破坏地估算其生物量提供有效途径,对深入探究各器官营养成分分布提供一定的理论基础。
槟榔(Areca catechu L.)为棕榈科(Palmaceae)槟榔属(Areca)多年生常绿木本植物,原产于热带、亚热带地区,是典型的热带雨林植物[11]。槟榔是海南具有垄断性的热带经济作物[12],目前已发展成为海南省第二大热带经济作物,总产值100亿元以上[13]。槟榔具有极高经济效益,是农户脱贫致富的重要经济作物,为70多万种植户、200万从业人员提供收入,成为海南主要经济支柱产业之一[13]。然而,在槟榔的种植生产上,农户多采用传统的“人种天管”的种养模式[14],大部分农户对槟榔园区的槟榔营养状况不清楚,为了提高产量,盲目增加施肥量,容易引起过量施肥的现象,不仅造成环境资源的浪费,还影响着植株的正常生长,严重时甚至烧伤槟榔根部[15]。施肥不合理导致肥料利用率低下,甚至引起槟榔植株病害,落果严重,品质低下,严重限制产量[12]。所以,为了提高槟榔产量和品质,同时又需要保护人类赖以生存的生态环境,科学、高效地使用肥料是当前主要解决途径[16]。本研究通过生物量模型,预测槟榔地上部分各器官干物质的积累量,结合植株营养元素的测定,探究槟榔养分分布和吸收规律,根据土壤供肥能力,可为判断槟榔营养的缺失提供理论依据,在作物营养供应的各个环节上,最大限度地提高肥料利用效率[17],从而在生产上达到精准施肥,提高槟榔的产量和品质,达到科学施肥及减肥增效的目的。
1 材料与方法
1.1 材料
试验样品取自海南省儋州市、万宁市、定安县和琼中县挂果槟榔园,槟榔植株为自然生长状态下9~11龄挂果槟榔树,4个地区土壤综合基本情况见表1,土壤肥力中等,种植密度为3 m(行距)×2 m(间距)。对54株槟榔样株进行全挖处理,将观测获得的54组数据均匀且完全随机地划分为3组,其中2组(36株)用于模型建立,1组(18株)用于模型的外部验证。对全挖处理槟榔植株进行分段处理,将槟榔茎杆、叶片用干毛巾擦拭干净。
1.2 方法
株高和茎粗是植株生物量的主要影响指标[18],本实验选取了槟榔植株较易测量参数和主要影响参数作为主要测定指标。包括槟榔全株的叶片数量(LN)、花苞数量(BN)、茎节数(NN)、茎节长度(IL)、0 m茎粗(SD0)、0.5 m茎粗(SD0.5)、1 m茎粗(SD1.0)、1.5 m茎粗(SD1.5)、茎高(SH)和株高(PH),以及每片叶片的叶长(LL)、叶宽(LW)(用软尺测量),用电子台秤对槟榔叶以及花器官称量总鲜重,对茎杆分区段称量茎杆总鲜重[8-9]。记录整株槟榔茎杆总鲜重、叶总鲜重以及地上部分总鲜重。将形态学指标调查之后的槟榔茎杆、叶以及花苞分别随机且均匀地取1.5 kg鲜样,置于恒温干燥箱内,105 ℃杀青30 min,随后80 ℃烘干至恒重,运用公式(1)换算出整株槟榔茎杆干物质积累总质量、叶片干物质积累总质量以及地上部分总干物质积累总质量。
1.3 数据处理
采用JMP 10、Office 2016、IBM SPSS Statistics 20、Graphpad Prism 6.02软件进行模型拟合、数据处理及分析。
2 结果与分析
2.1 各形态指标之间的相关性分析
对槟榔植株各形态指标进行相关性分析,发现0 m茎粗(SD0)和0.5 m茎粗(SD0.5)、0.5 m茎粗(SD0.5)和1 m茎粗(SD1.0)、1 m茎粗(SD1.0)和1.5 m茎粗(SD1.5),以及茎高(SH)和株高(PH)之间呈现出高度相关,相关系数大于0.8500,Pearson相关性均达0.01水平(表2)。
2.2 槟榔茎杆干物质积累量的数学模型构建与检验
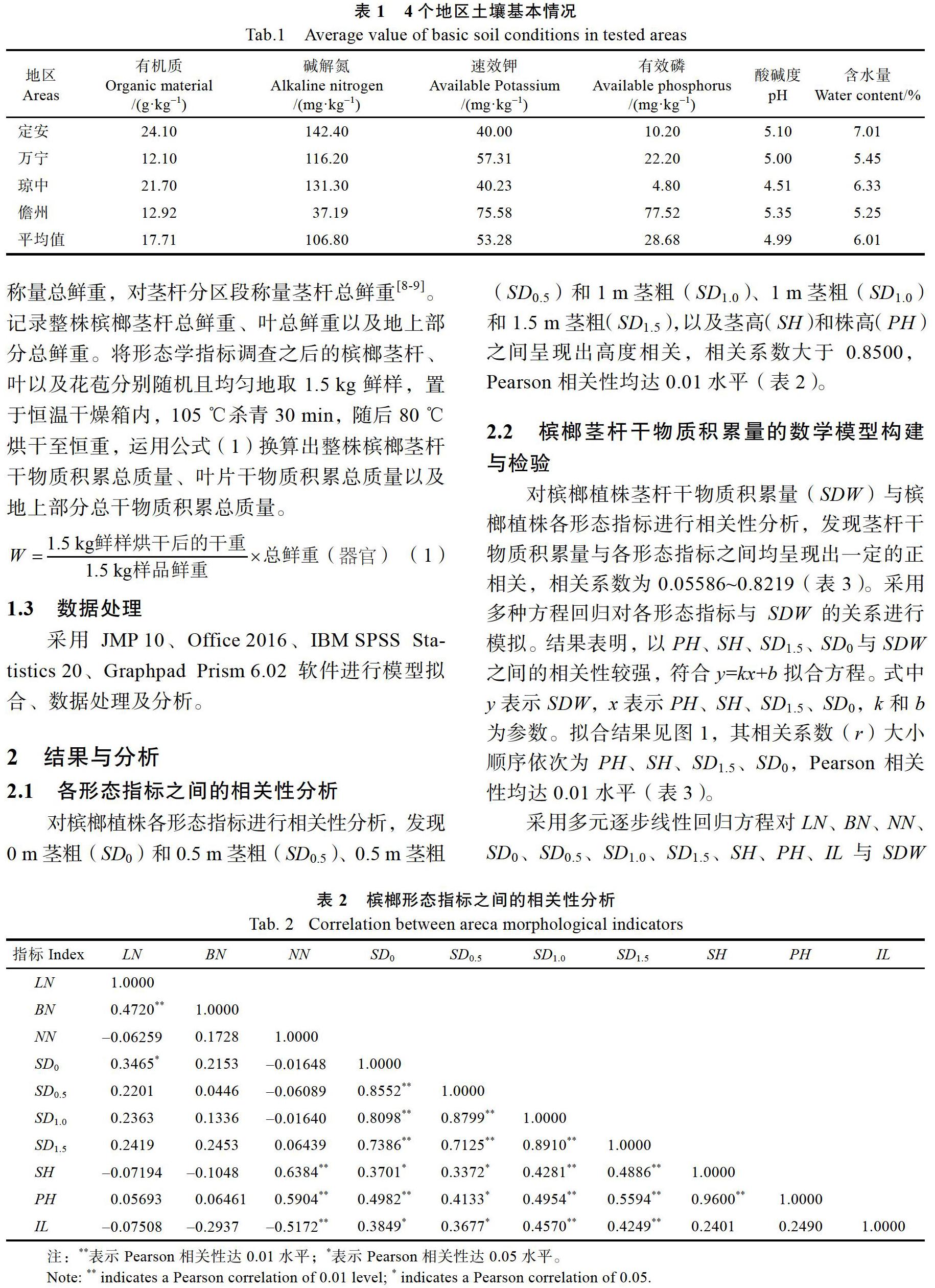
对槟榔植株茎杆干物质积累量(SDW)与槟榔植株各形态指标进行相关性分析,发现茎杆干物质积累量与各形态指标之间均呈现出一定的正相关,相关系数为0.05586~0.8219(表3)。采用多种方程回归对各形态指标与SDW的关系进行模拟。结果表明,以PH、SH、SD1.5、SD0与SDW之间的相关性较强,符合y=kx+b拟合方程。式中y表示SDW,x表示PH、SH、SD1.5、SD0,k和b为参数。拟合结果见图1,其相关系数(r)大小顺序依次为PH、SH、SD1.5、SD0,Pearson相关性均达0.01水平(表3)。
采用多元逐步线性回归方程对LN、BN、NN、SD0、SD0.5、SD1.0、SD1.5、SH、PH、IL与SDW的关系进行模拟。结果表明,以SD0、PH构建预测SDW的数学模型较优,得到预测槟榔茎杆干物质积累量的模型(公式(2))。模型拟合效果,决定系数R2=0.7157,均方根误差RMSE=6.492。F值检验结果表现为显著(P<0.0001)。
SDW=0.2518 SD0+0.0423 PH23.8883 (2)
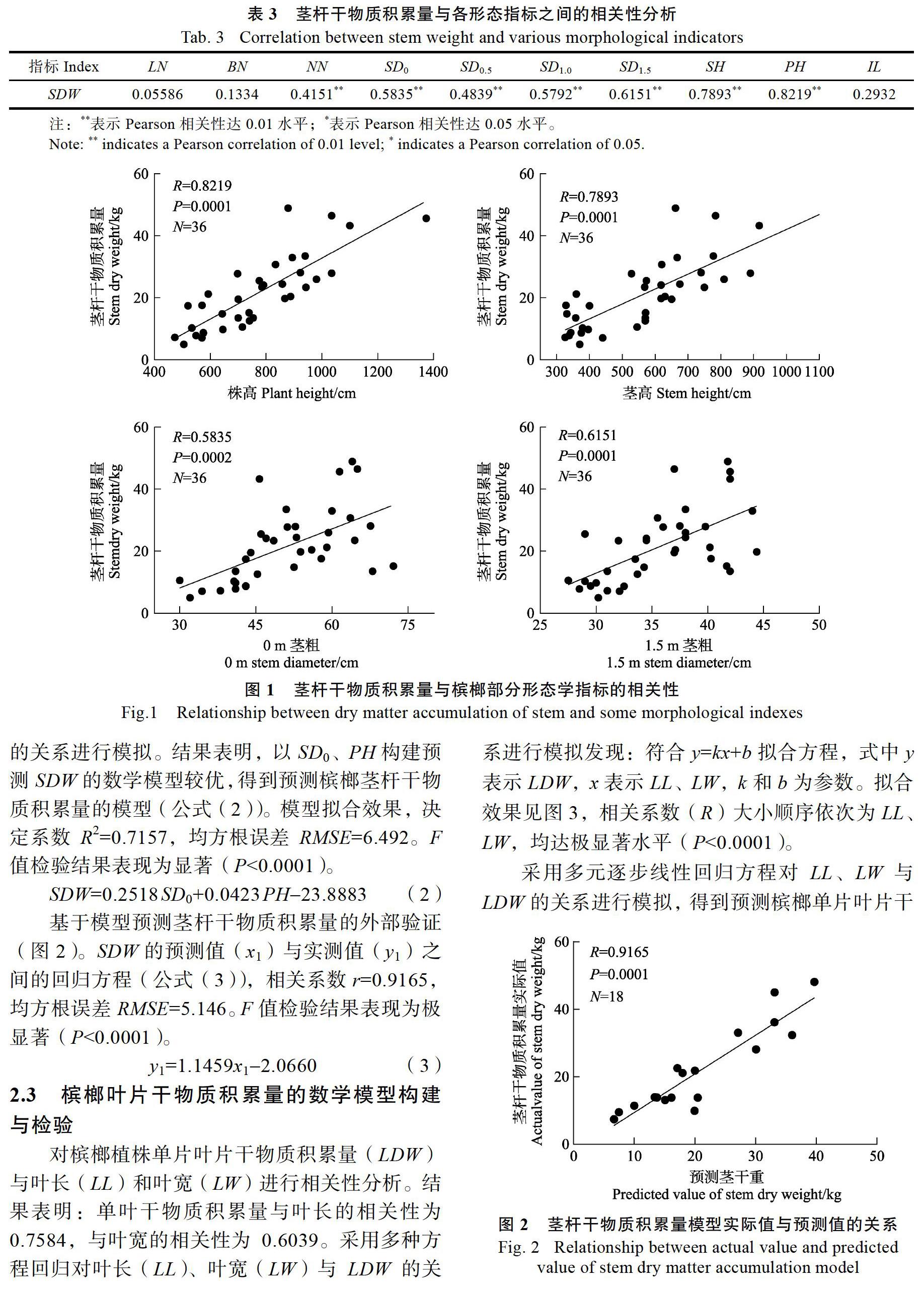
基于模型预测茎杆干物质积累量的外部验证(图2)。SDW的预测值(x1)与实测值(y1)之间的回归方程(公式(3)),相关系数r=0.9165,均方根误差RMSE=5.146。F值检验结果表现为极显著(P<0.0001)。
y1=1.1459x12.0660 (3)
2.3 槟榔叶片干物质积累量的数学模型构建与检验
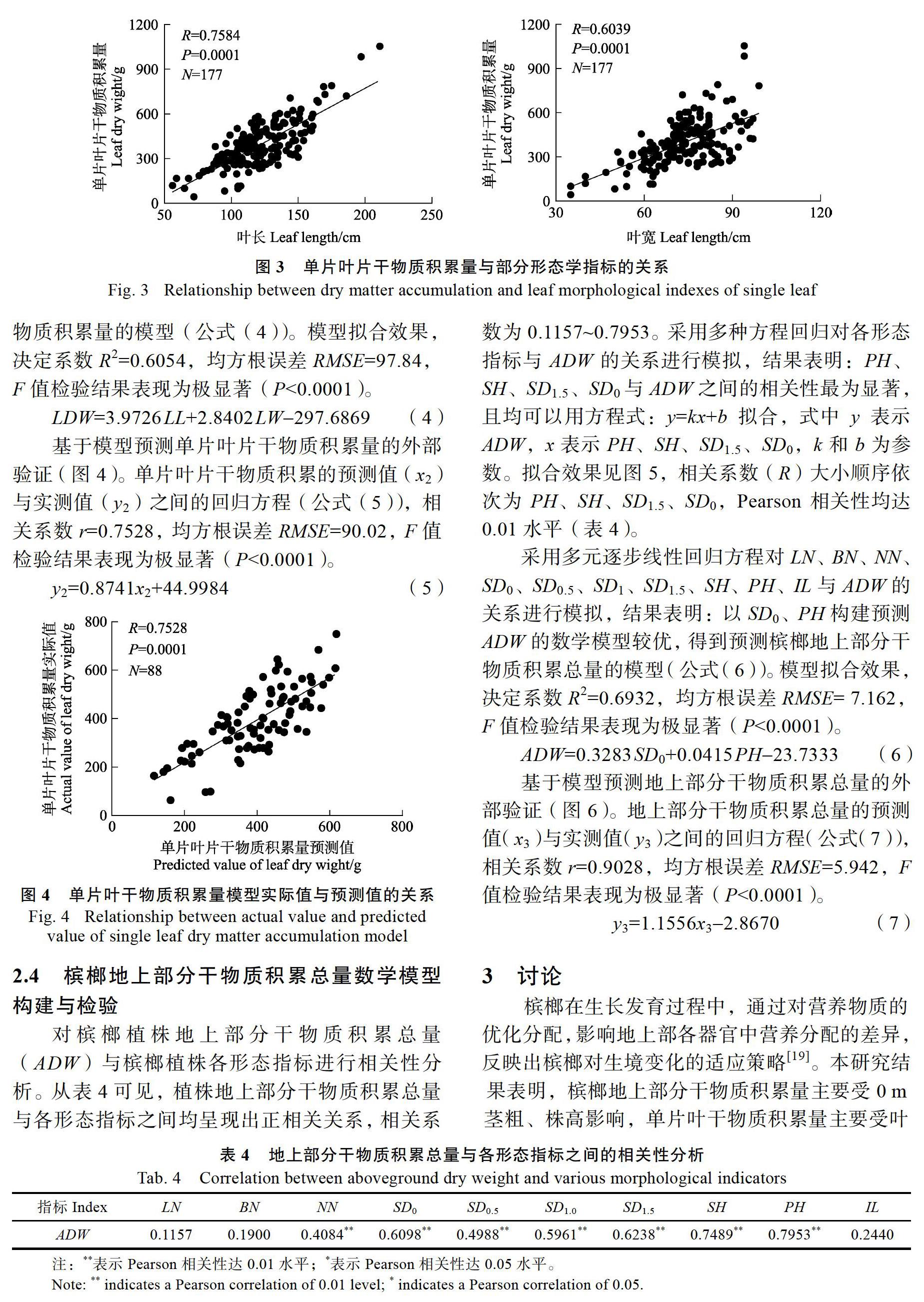
对槟榔植株单片叶片干物质积累量(LDW)与叶长(LL)和叶宽(LW)进行相关性分析。结果表明:单叶干物质积累量与叶长的相关性为0.7584,与叶宽的相关性为0.6039。采用多种方程回归对叶长(LL)、叶宽(LW)与LDW的关系进行模拟发现:符合y=kx+b拟合方程,式中y表示LDW,x表示LL、LW,k和b为参数。拟合效果见图3,相关系数(R)大小顺序依次为LL、LW,均达极显著水平(P<0.0001)。
采用多元逐步线性回归方程对LL、LW与LDW的关系进行模拟,得到预测槟榔单片叶片干物质积累量的模型(公式(4))。模型拟合效果,决定系数R2=0.6054,均方根误差RMSE=97.84,F值检验结果表现为极显著(P<0.0001)。
LDW=3.9726 LL+2.8402 LW297.6869 (4)
基于模型预测单片叶片干物质积累量的外部验证(图4)。单片叶片干物质积累的预测值(x2)与实测值(y2)之间的回归方程(公式(5)),相关系数r=0.7528,均方根误差RMSE=90.02,F值检验结果表现为极显著(P<0.0001)。
y2=0.8741x2+44.9984 (5)
2.4 槟榔地上部分干物质积累总量数学模型构建与检验
对槟榔植株地上部分干物质积累总量(ADW)与槟榔植株各形态指标进行相关性分析。从表4可见,植株地上部分干物质积累总量与各形态指标之间均呈现出正相关关系,相关系数为0.1157~0.7953。采用多种方程回归对各形态指标与ADW的关系进行模拟,结果表明:PH、SH、SD1.5、SD0与ADW之间的相关性最为显著,且均可以用方程式:y=kx+b拟合,式中y表示ADW,x表示PH、SH、SD1.5、SD0,k和b为参数。拟合效果见图5,相关系数(R)大小顺序依次为PH、SH、SD1.5、SD0,Pearson相关性均达0.01水平(表4)。
采用多元逐步线性回归方程对LN、BN、NN、SD0、SD0.5、SD1、SD1.5、SH、PH、IL与ADW的关系进行模拟,结果表明:以SD0、PH构建预测ADW的数学模型较优,得到预测槟榔地上部分干物质积累总量的模型(公式(6))。模型拟合效果,决定系数R2=0.6932,均方根误差RMSE= 7.162,F值检验结果表现为极显著(P<0.0001)。
ADW=0.3283 SD0+0.0415 PH23.7333 (6)
基于模型预测地上部分干物质积累总量的外部验证(图6)。地上部分干物质积累总量的预测值(x3)与实测值(y3)之间的回归方程(公式(7)),相关系数r=0.9028,均方根误差RMSE=5.942,F值检验结果表现为极显著(P<0.0001)。
y3=1.1556x32.8670 (7)
3 讨论
槟榔在生长发育过程中,通过对营养物质的优化分配,影响地上部各器官中营养分配的差异,反映出槟榔对生境变化的适应策略[19]。本研究结果表明,槟榔地上部分干物质积累量主要受0 m茎粗、株高影响,单片叶干物质积累量主要受叶长和叶宽的影响;茎杆干物质拟合效果>地上部分总干物质拟合效果>叶片干物质拟合效果。槟榔茎杆干物質量的估测模型为SDW=0.2518 SD0+ 0.0423 PH23.8883,决定系数R2=0.7157,均方根误差RMSE=6.492,F值检验结果表现为极显著(P<0.0001),外部验证结果相关系数r=0.9165;槟榔地上部分总干物质量的估测模型为ADW=0.3283 SD0+0.0415 PH23.7333,决定系数R2=0.6932,均方根误差RMSE=7.162,F值检验结果表现为极显著(P<0.0001),外部验证结果相关系数r=0.9028;槟榔单片叶片干物质量的估测模型为LDW=3.9726 LL+2.8402 LW297.6869,决定系数R2=0.6054,均方根误差RMSE=97.84,F值检验结果表现为极显著(P<0.0001),外部验证结果相关系数r=0.7528。
植株地上部分株高和茎粗是反映植株生物量的重要指标之一[18],黄润霞等[19]在研究木榄生物量模型时发现,木榄各器官及全株生物量与基茎之间存在较强的一次函数相关性,且决定系数较高,在引入株高之后可在一定程度上提高预测模型的拟合效果,提高预测精度[20]。范航清等[21]在研究广西海岸白骨壤红树植物地上部生物量的相关分析时发现,白骨壤红树地上部分干物质积累量与株高、茎粗等密切相关。株高、基部茎粗是植株地上部分干物质积累的主要影响因素 [22-24],这一结果与本研究吻合。但是以株高、茎粗拟合不同植株干物质积累量时表现出的函数关系不尽相同,在对灌木、竹类、乔木等植物研究中,多表现为茎粗、株高与植株干物质积累量成幂函数或指数函数关系[8,25-29],赵梦颖等[30]对内蒙古26种温带灌木最优生物量方程研究发现,株高等形态指标与生物量主要表现出幂函数和一元线性函数关系。
槟榔地上部分总干物质积累量主要受0 m茎粗、株高影响,槟榔茎杆干物质积累量主要受株高、0 m茎粗的影响,槟榔单片叶片干物质积累量主要受叶长和叶宽的影响,本研究可以通过测量槟榔0 m茎粗和株高来预测槟榔地上部分干物质积累量,也可以通过测量掉落槟榔叶的叶长和叶宽来预测叶片干物质量,判断其干物质量的丢失情况,为后续生产实践上的指导施肥提供一定的理论依据。但本研究对槟榔茎杆、叶以及地上部分各器官生物量的拟合精度分别仅为71.57%、60.54%、69.32%,生物量预测模型对茎杆、叶、地上部分生物量的拟合精度较低,在野外取样的过程中,对全株槟榔的取样上存在一定的难度,导致样本数量较少,从而对预测模型的精度产生影响。为了进一步提高预测模型的精度,在今后工作中应尽可能提高样本数量以获取更多的数据。
参考文献
[1] 杨昊天, 李新荣, 王增如, 等. 腾格里沙漠东南缘4种灌木的生物量预测模型[J]. 中国沙漠, 2013, 33(6): 1699-1704.
[2] 杨昊天, 李新荣, 刘立超, 等. 荒漠草地4种灌木生物量分配特征[J]. 中国沙漠, 2013, 33(5): 1340-1348.
[3] 仇 瑶, 常顺利, 张毓涛, 等. 天山林区六种灌木生物量的建模及其器官分配的适应性[J]. 生态学报, 2015, 35(23): 7842-7851.
[4] 冯 丽, 张景光, 张志山, 等. 腾格里沙漠人工固沙植被中油蒿的生长及生物量分配动态[J]. 植物生态学报, 2009, 33(6): 1132-1139.
[5] 郭子武, 章 超, 杨丽婷, 等. 提前钩梢对雷竹地上构件生物量分配及其异速生长关系的影响[J]. 生态学报, 2020, 40(2): 711-718.
[6] 李红丽, 智颖飙, 赵 磊, 等. 大米草(Spartina anglica)自然衰退种群对N、P添加的生态响应[J]. 生态学报, 2007, 27(7): 2725-2732.
[7] 张 倩. 塔里木河上游胡杨林地上生物量动态遥感监测[D]. 贵阳: 贵州大学, 2018.
[8] 刘景贵. 乔木生物量建模样本采集细节探讨[J]. 林业科技情报, 2014, 46(4): 68-69.
[9] 王广民, 李 庆, 吴焕荣, 等. 森林资源连续清查森林生物量建模乔木样本外业采集[J]. 山东林业科技, 2011, 41(1): 78-79, 102.
[10] 罗洪斌, 舒清态, 王 强, 等. 运用机载激光雷达和陆地卫星数据对橡胶林地上生物量的估测[J]. 东北林业大学学报, 2019, 47(7): 56-61.
[11] 黄慧德. 2015年槟榔产业发展报告及形势预测[J]. 世界热带农业信息, 2017(1): 31-39.
[12] 杨福孙, 孙爱花, 边子星, 等. 施肥对槟榔坐果率及产量的影响[J]. 安徽农业科学, 2015, 43(22): 23-25.
[13] 孙慧洁, 龚 敏. 海南槟榔种植、加工产业发展现状及对策研究[J]. 热带农业科学, 2019, 39(2): 91-94.
[14] 江湛钰. 海南槟榔业发展的现状及技术创新中存在的问题[J]. 中国商论, 2016(16): 137-138.
[15] 符之学. 万宁市槟榔种植业现状及健康持续发展措施[J]. 现代农业科技, 2018(9): 123-124.
[16] Bindraban P S, Dimkpa C, Nagarajan L, et al. Revisiting fertilisers and fertilisation strategies for improved nutrient uptake by plants[J]. Biology and Fertility of Soils, 2015, 51(8): 897-911.
[17] 白由路. 高效施肥技术研究的现状与展望[J]. 中国农业科学, 2018, 51(11): 2116-2125.
[18] 郭佳伟. 狭叶甜茅群落对增温和氮输入及其交互作用的响应研究[D]. 长春: 中国科学院研究生院(东北地理与农业生态研究所), 2015.
[19] 黄润霞, 吴卓翎, 彭江炜, 等. 广东红树植物木榄生物量模型[J]. 西北农林科技大学学报(自然科学版), 2019, 47(12): 1-10.
[20] 董利虎, 李凤日, 宋玉文. 东北林区4个天然针叶树种单木生物量模型误差结构及可加性模型[J]. 应用生态学报, 2015, 26(3): 704-714.
[21] 范航清, 尹 毅, 勞丽荣. 广西海岸白骨壤红树植物地上部生物量的相关分析[J]. 广西科学院学报, 1993(2): 25-30.
[22] 施鹏程. 三峡库区乔木生物量和碳储量研究[D]. 北京: 北京林业大学, 2014.
[23] 杨 潇. 内蒙古大青山主要森林植被生产力与碳储量研究[D]. 呼和浩特: 内蒙古农业大学, 2013.
[24] 周再知, 郑海水, 尹光天, 等. 橡胶树生物量估测的数学模型[J]. 林业科学研究, 1995(6): 624-629.
[25] 李晓明, 杨重法, 左应梅, 等. 估测木薯茎叶生物量的一数学模型[J]. 热带作物学报, 2009, 30(4): 440-444.
[26] 郑郁善, 陈 辉, 张炜银. 绿竹生物量优化模型建立研究[J]. 经济林研究, 1998(3): 4-7, 70.
[27] 曹 梦, 潘 萍, 欧阳勋志, 等. 天然次生林中闽楠生物量分配特征及相容性模型[J]. 浙江农林大学学报, 2019, 36(4): 764-773.
[28] 姚正阳, 刘建军. 西安市4种城市绿化灌木单株生物量估算模型[J]. 应用生态学报, 2014, 25(1): 111-116.
[29] 汪珍川, 杜 虎, 宋同清, 等. 广西主要树种(组)异速生长模型及森林生物量特征[J]. 生态学报, 2015, 35(13): 4462-4472.
[30] 赵梦颖, 孙 威, 罗永开, 等. 内蒙古26种常见温带灌木的生物量模型[J]. 干旱区研究, 2019, 36(5): 1219-1228.
