弃杆组概念的运动学矢量方程拼图解法

李春明,尹晓丽,刘 庆

(1.中国石油大学(华东) 中国石油大学胜利学院,山东 东营 257061;2.中国石油大学(华东) 机电工程学院,山东 青岛 266580)

自人类使用工具以来,机械学科逐渐发展起来。机械原理研究机械的结构[1]、运动[2]、受力[3]、振动[4]等,成长为理论丰富、体系完善的学科。在结构方面,多杆机构、多级杆组、多级机构在理论体系中仍占有一席之地;在动力学方面,依据理论力学知识的运动学参数矢量方程图解法获得广泛应用。但是,随着机构组合理论的完善,杆组的概念逐渐被质疑;随着各类运动学分析方法的发展,矢量方程图解法难以求解的问题逐渐引起学者重视。

研究分析杆组及高级机构的组合形式,并针对一个串连组合机构的运动学问题研究每个矢量方程均不能采用矢量方程图解法求解的问题。

1 基于机构组合的杆组概念舍弃

杆组的概念是机械原理学科的一部分内容,构件(构体)和运动副组成的组合称为杆组。将机构划分为不同的杆组,杆组的最高级别就是机构的级别。杆组和机构的等级越高说明机构越复杂。

如果从机构组合的角度研究,存在高级杆组的平面机构均可以视为由基本的平面四杆机构组合而成的机构,如图1所示[5]。

图1(a)可视为:曲柄滑块机构与双滑块机构所组成的串联机构,前置机构的连杆与后置机构的导杆连结;图1(b)可视为:凸轮机构、双摇杆(或双曲柄)机构和双滑块机构所组成的串连组合机构,第1前置机构的摆动从动件与第2前置机构的连杆连结,第2前置机构的从动摇杆与后置机构的导杆连结,弹簧保证凸轮与从动件始终接触;图1(c)可视为:曲柄摇杆机构与摇杆滑块机构所组成的串连组合机构,前置机构的摇杆与后置机构的摇杆连结;图1(d)可视为:解放机架(固定体)的曲柄摇杆机构与凸轮机构所组成的封闭组合机构,前者为基础机构,后者为附加机构,二者有2个构件分别连结;图1(e)可视为:解放机架的摇块机构和曲柄摇杆机构所组成的封闭组合机构,前者为2个独立运动的基础机构,后者为单独立运动的附加机构,前者解放的机架与后者的摇杆连结;图1(f)可视为:2个独立运动连杆机构与单独立运动轮系所组成的封闭组合机构,二者有2个构件连结;图1(g)可视为:2个独立运动连杆机构与双摇杆机构所组成的封闭组合机构,再与凸轮机构串联的复合式组合机构。

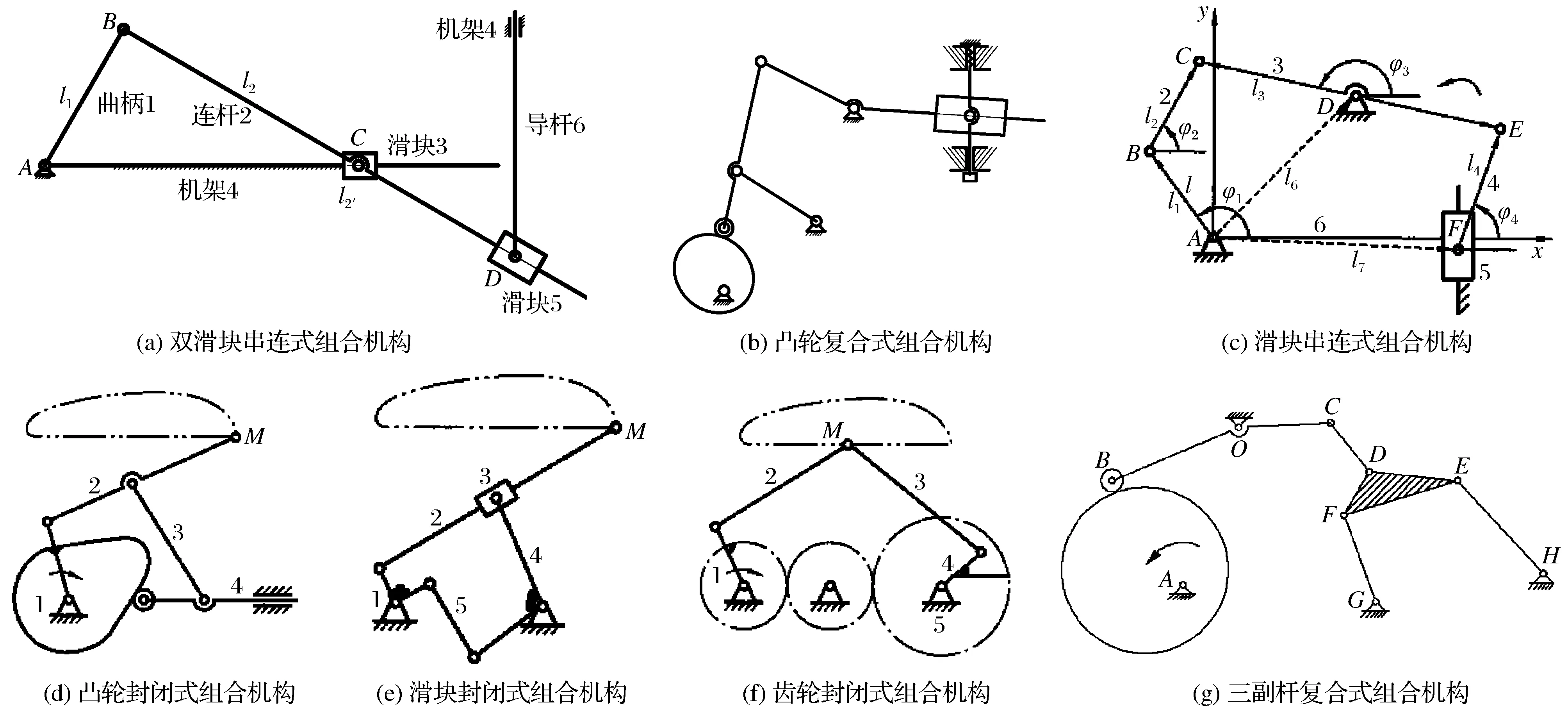
图1 7个高级机构Fig.1 7 high-level mechanisms

2 组合机构的运动学参数矢量方程

构件的运动学参数主要依据理论力学的2个运动关系所列出的矢量方程求解:

(1) 同一刚体上两点之间的运动关系。刚体上任一点的运动等于随基点的平动和绕基点的转动之和。绕基点的相对转动角速度和角加速度为构件的角速度和角加速度。

(2) 两构件重合点之间的速度和加速度关系。动点的运动等于牵连点的运动与相对运动之和。科式加速度是由于牵连运动为转动而产生的附加加速度,可由矢量的数学推导求出。

如果速度(加速度)矢量图的极点均表示速度(加速度)为零的点,且各点与极点的相对位置表示该点的速度(加速度),则构件图与速度(加速度)矢量图上相对应的图形相似,且表示点的字母绕行方向一致。根据该特点确定构件上未知点速度(加速度)的方法,称为速度(加速度)影像法。

对于图1(a)所示的组合机构,可列出以下速度(加速度)矢量方程:

(1) 构件2、构件5重合点的相对运动关系矢量方程。

(2) 构件2上,D点相对于C点的相对运动矢量方程。

(3) 构件2上,D点相对于B点的相对运动矢量方程。

(4) 构件2上,C点相对于B点的相对运动矢量方程。

设构件1为主动件(体),即运动参数已知,则已知参数为B点的速度(加速度)大小和方向、C点的速度(加速度)方向、构件5上D点的速度(加速度)方向。设构件6为主动件,则已知参数为构件5上D点的速度(加速度)大小和方向、构件2上C点的速度(加速度)方向、B点的速度(加速度)方向。

根据矢量方程的几何意义,由图1(a)可得2个位置矢量方程[6-7]:

(1)

可得投影方程组[8-10]:

(2)

如果构件1为主动件,则未知量为lB2D、θ2、x2,6;如果构件6为主动件,则未知量为θ1、lB2D、θ2,2种情况的方程数和未知量数均相等,可解。

3 倒置机构的矢量方程图解法难点

对于图1(a)所示的组合机构,通常,构件1为主动件,在构件2上C点相对于B点的相对运动矢量方程中,只存在2个未知量,可由矢量方程图解法求解。然后,又出现只含2个未知量的矢量方程,逐个求解之后,可获得全部构件的运动学参数。

如果采用机构倒置的创新方法,将主动件改换为构件6,则不存在只含2个未知量的矢量方程,各矢量方程均难以用图解法求解。

(1) 构件2、构件5重合点D的相对运动速度矢量方程为

(3)

(2) 构件2上D点相对于C点、B点的速度矢量方程分别为

(4)

(5)

(3) 构件2上C点相对于B点的速度矢量方程为

(6)

加速度矢量方程与速度矢量方程的未知量相同,也难以逐个求解。

4 基于几何意义的拼结图解法

对于图1(a)所示的机构,以A为坐标原点,以水平往右为x1轴正方向建立x1-x2直角坐标系。设机构参数如下:

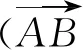
(7)

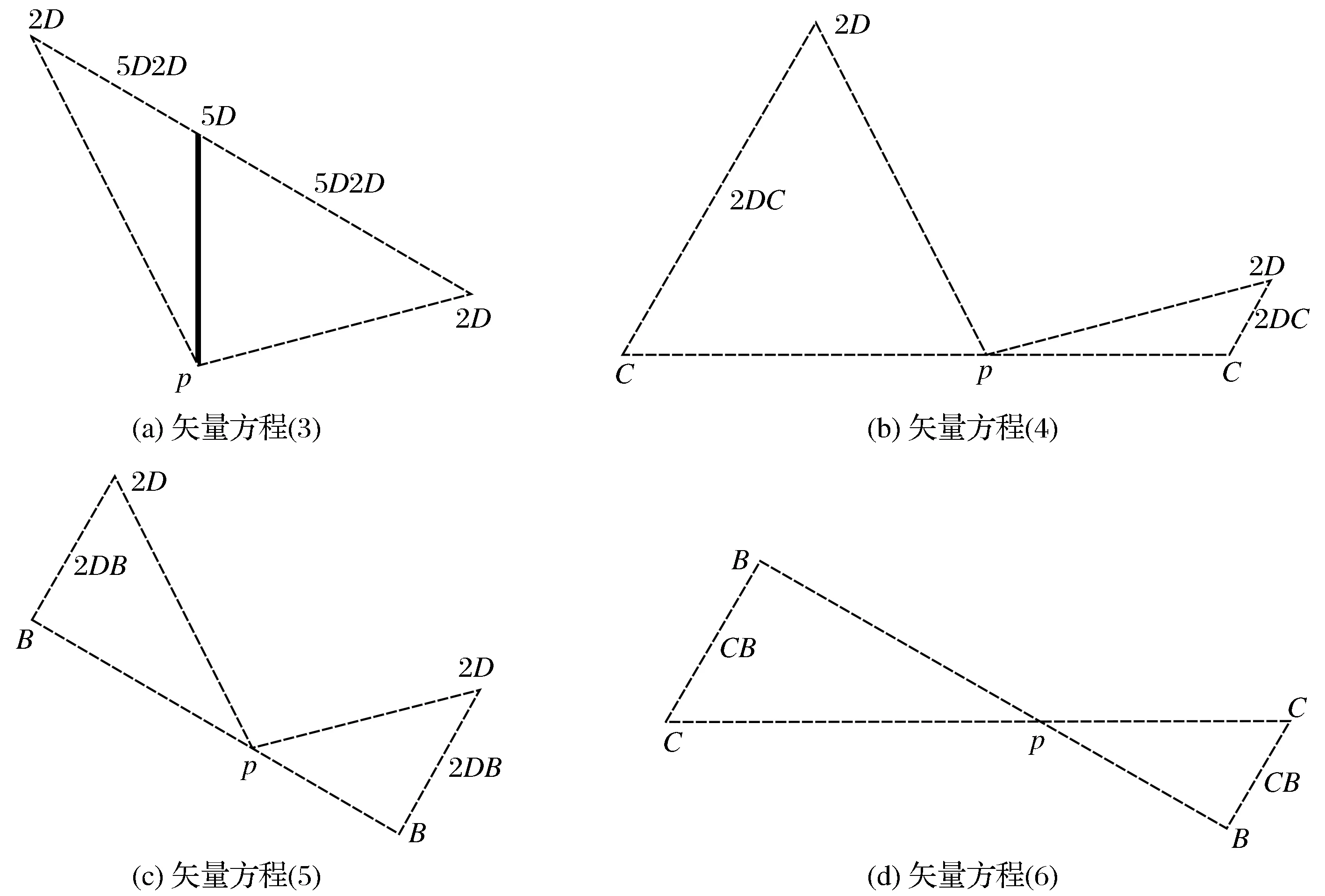
图2 4个矢量方程的矢量图Fig.2 Graphs of 4 vector equations

采用标准的速度(加速度)矢量图,即极点表示速度(加速度)为零的点,将图2的4个图拼为1张,如图3所示。根据速度(加速度)影像法的原理,以及构件2的结构形状,右边的图符合实际情况,因此,左边的图须舍弃。

根据图1(a)的几何关系,可根据正弦定理、余

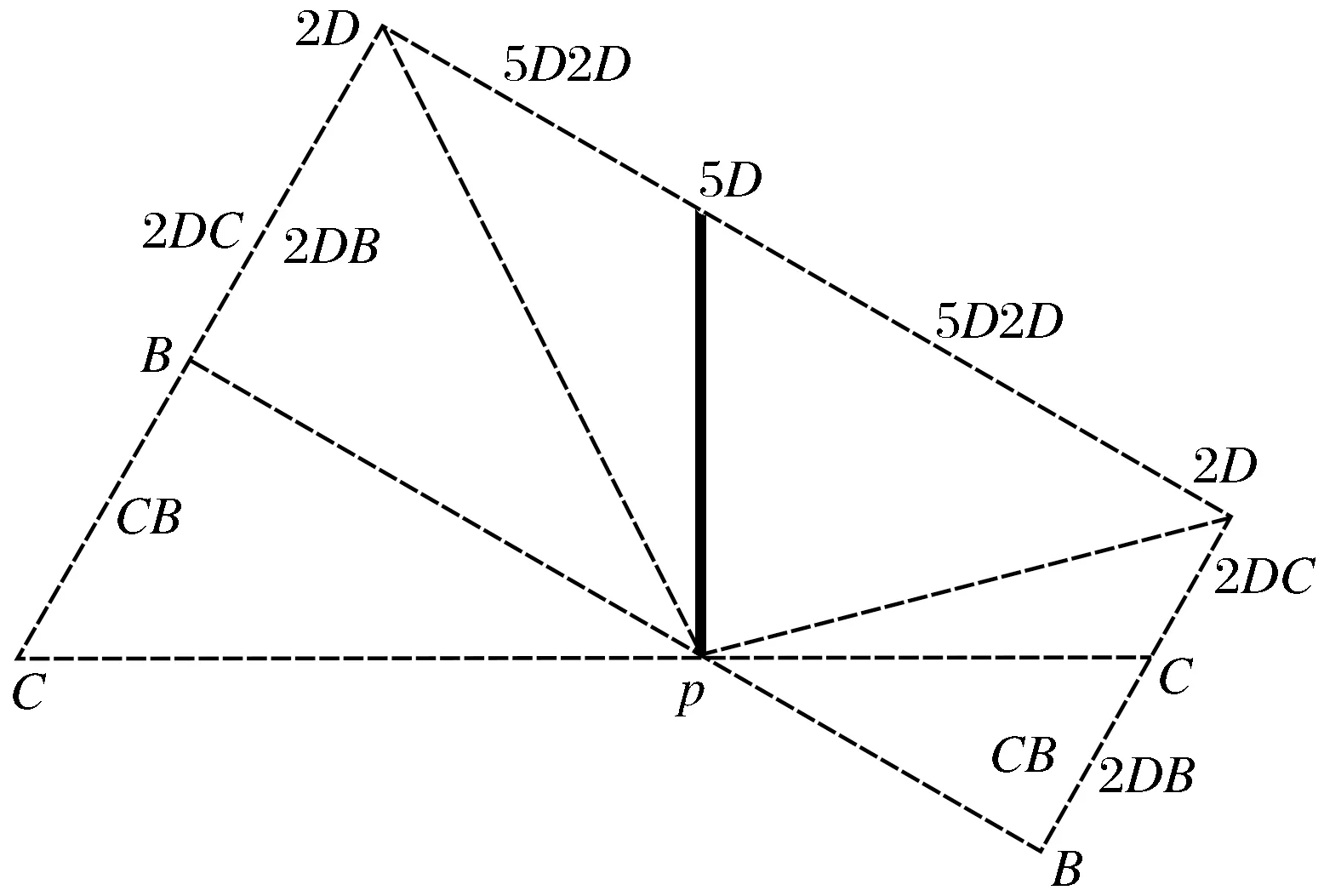
图3 直接拼接的图Fig.3 Graph spliced directly

弦定理、勾股定理等获得以下几何参数:

(8)

对于机构的一般位置,上述尺寸可在图1(a)中测出,图1(a)的绘图顺序为:

(1) 绘出固定铰接点A、滑块3、滑块5的导路;

(2) 根据θ1绘出B;

(3) 以B为圆心,以l2为半径画弧,与滑块3的导路交于C点;

(4) 延长BC,与滑块5的导路交于D点。

(9)

根据速度(加速度)影像法的原理,以及构件2上B、C、D3点之间的比例关系,可得

(10)

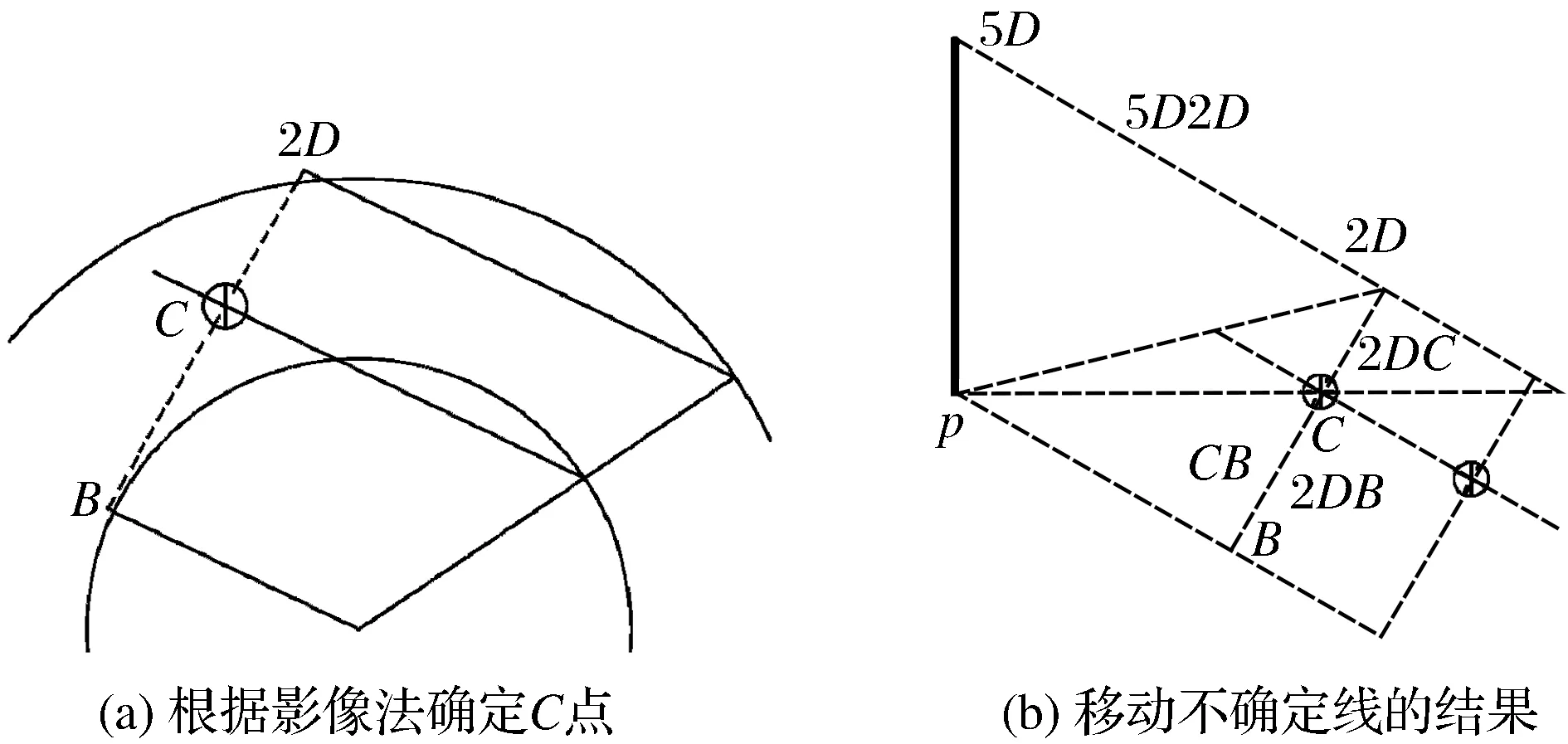
图4 拼图解法的图Fig.4 Graph of puzzle solution

(11)

求得速度矢量之后,加速度矢量方程组的科式加速度、向心加速度、相对向心加速度均可求出,其拼图求解过程与速度矢量方程组的相同。

5 结论

(1) 解析法能求解的机构运动学问题,也能用矢量方程图解法求解。研究提出的拼图解法解决了每个矢量方程均不能采用图解法求解的机构运动学问题。

(2) 借助于计算机绘图软件,图解法的求解结果可达到解析法的精度。

(3) 平面高级机构均可视为平面四杆机构经过组合而成的组合机构。杆组和高级机构的概念可舍弃。