E型倾斜腔体内纳米流体自然对流数值研究
2020-10-29金淑英马兵善
金淑英,马兵善,王 刚
(兰州理工大学土木工程学院,甘肃 兰州 730050)
在太阳能集热器、电子设备冷却、换热器和空调系统等工程应用领域中均会遇到自然对流换热现象,由于该现象的广泛存在性及实际重要性,许多学者已对其开展了大量的研究工作,取得了丰硕的成果。
实际工程中涉及的自然对流换热现象均采用水、油等传统液体作为工作介质,而传统液体的导热系数低,限制了自然对流传热速率的进一步提高。传统液体的换热性能可以通过悬浮在流体中的纳米颗粒来提高,这种悬浮有纳米颗粒的流体被称为纳米流体。自从美国Argonne国家实验室的Choi[1]首次提出纳米流体的概念之后,国内外已经有很多学者对纳米流体是否能够强化自然对流换热开展了大量的研究工作。Khanafer等[2]率先采用数值模拟方法,研究了方腔内的Cu-水纳米流体自然对流换热,结果表明纳米流体可以强化自然对流换热,并分析出在给定格拉晓夫数(Gr)条件下,传热速率随纳米颗粒体积分数的增加而增加。之后,很多学者从不同的角度对纳米流体自然对流换热进行了研究。Abu-Nada等[3]通过数值研究了倾斜腔体内Cu-水纳米流体自然对流,结果表明,添加纳米颗粒可有效改善传热,而且和Ra数较大时的传热速率对比,Ra数较小时强化传热的效果更好;当腔体倾角为90°时,传热效果最差;当Ra数较大时,纳米流体的传热强化百分率随着倾角的增加而减小。形状不同的腔体内纳米流体自然对流换热的研究也受到了关注。Mahmoodi等[4]对C形腔体内Cu-水纳米流体自然对流换热进行了数值研究,他们发现采用纳米流体作为传热工质可以强化自然对流换热。王杰等[5]采用数值模拟方法对凹槽形腔体内TiO2-水纳米流体的自然对流换热进行了研究,也发现在水中添加纳米颗粒可以强化自然对流换热。
随着电子工业的发展,人们对散热系统的散热效率提出了更高的要求。分析国内外相关文献发现,利用纳米流体提高电子元器件自然对流散热效率的研究较少。因此,以下对E型腔体内Cu-水纳米流体的自然对流换热进行数值研究,并分析Ra数、腔体倾角以及纳米颗粒体积分数对自然对流换热特性的影响。
1 物理模型和控制方程
1.1 物理模型
从电子元器件散热设备中选取一个截面——E型腔体,研究其内纳米流体自然对流换热特性,E型腔体物理模型与坐标系统如图1所示。图1中的二维倾斜E型腔体内充满了Cu-水纳米流体,腔体恒温热壁面温度均为Th,恒温冷壁面温度均为Tc,且Th>Tc,其余壁面(如图1中填充部分的所有壁面)均为绝热壁面。腔体尺寸如图1所示,其中L/H=0.2,腔体倾角γ=0°~90°。水和Cu纳米颗粒的热物性参数见表1。
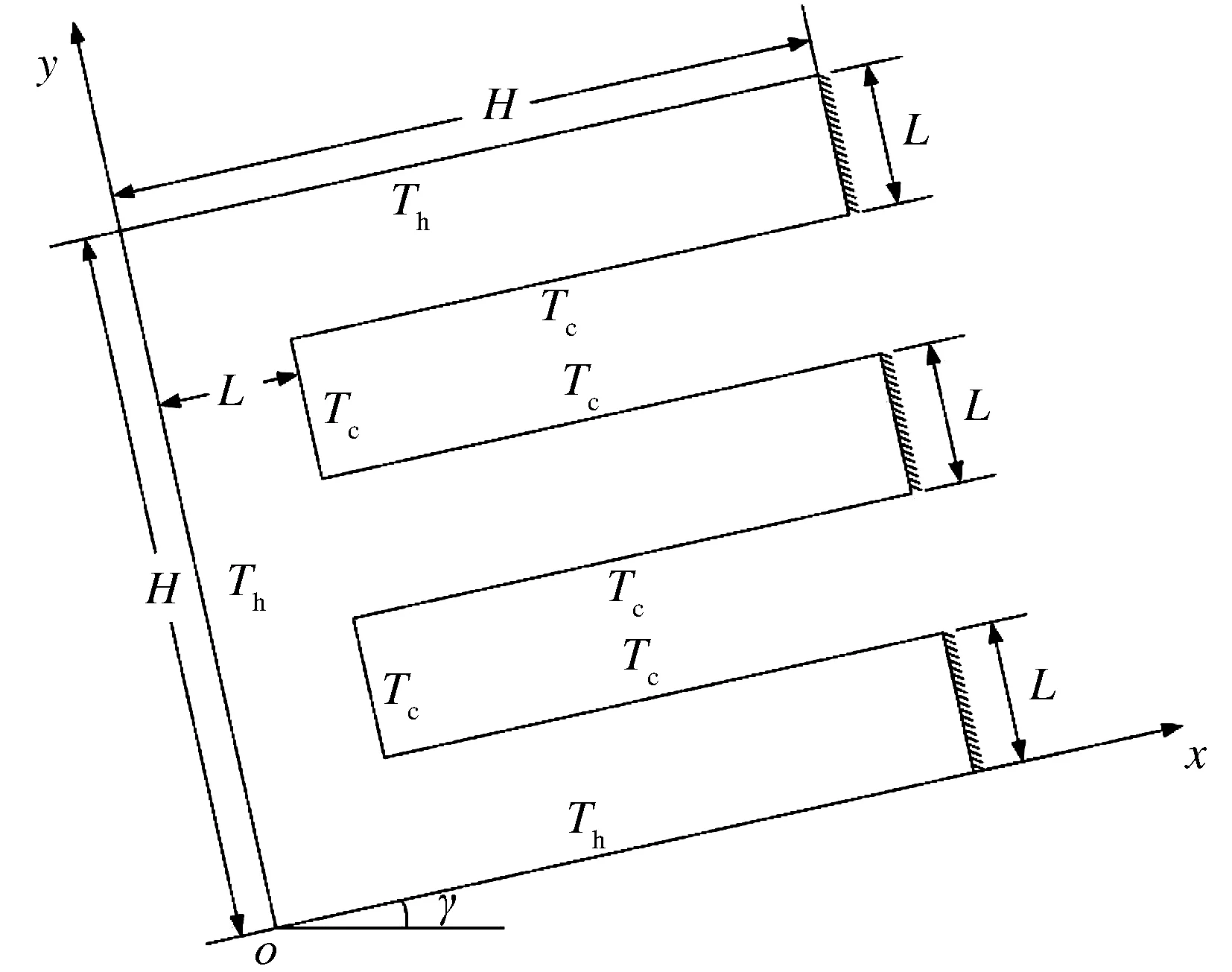
图1 物理模型与坐标系统Fig.1 Physical model and coordinate system
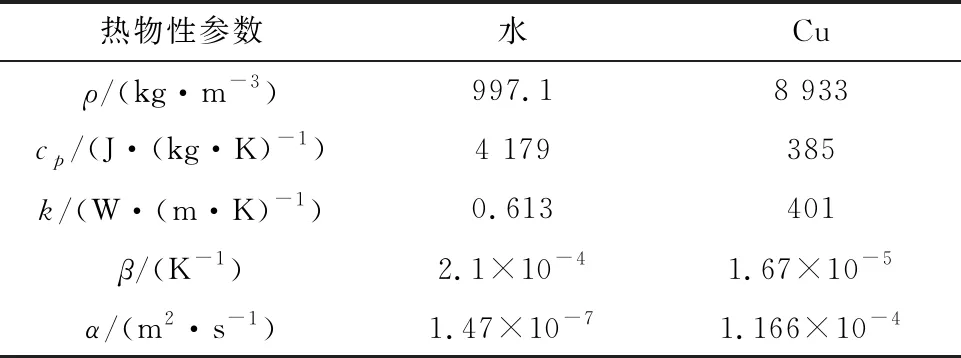
表1 水与Cu纳米颗粒的热物性参数
1.2 控制方程
在数值计算过程中,假设纳米流体为各向同性、不可压缩的牛顿流体,因浮升力引起的纳米流体密度的变化采用Boussinesq假设考虑;纳米颗粒与流体无相互滑动,纳米颗粒形状和纳米颗粒粒径分布均匀,纳米颗粒与基液处于热平衡状态;不考虑粘性耗散。二维倾斜E型腔体内纳米流体层流自然对流换热的无量纲控制方程分别为
(1)
(4)
方程(1)~(4)中涉及的无量纲量定义如下:
(5)
其中:下标f和nf分别代表纯水和纳米流体。纳米流体密度ρnf、纳米流体热容(ρcp)nf及纳米流体热膨胀系数βnf的计算公式[6]分别为
ρnf=(1-φ)ρf+φρnp,
(6)
(ρcp)nf=(1-φ)(ρcp)f+φ(ρcp)np,
(7)
βnf=(1-φ)βf+φβnp,
(8)
其中:下标np代表纳米颗粒;φ为纳米流体中纳米颗粒体积分数。纳米流体热扩散系数αnf计算公式[6]为
αnf=knf/(ρcp)nf。
(9)
纳米流体导热系数knf计算公式[7]为
(10)
纳米流体粘度μnf的计算公式[8]为
(11)
所研究问题相应的无量纲边界条件如下:
热壁面:U=V=0,θ=1,
冷壁面:U=V=0,θ=0,绝热壁面:U=V=0,∂θ/∂X=0。
(12)
无量纲流函数Ψ可以描述腔体内流体的流动强度,其定义为
(13)
努塞尔数是表征对流换热强烈程度的无量纲准则数。E型腔体热壁面平均努塞尔数Nuave的计算公式为
2 数值计算方法验证
研究采用SIMPLEC算法对无量纲控制方程进行求解,采用非均分网格,对流项采用具有较高精度的QUICK格式进行离散,使计算结果具有较高的准确性[9]。同时采用160×160、180×180、200×200、250×250及300×300共5种网格数进行网格独立性验证,通过计算发现网格数为200×200时获得网格独立解。
为了验证计算程序的准确可靠性,对文献[4]中所研究的宽高比为0.8的C型封闭腔体内Cu-水纳米流体的自然对流进行了数值求解,把计算得到的平均努塞尔数Nuave与文献[4]中的相应值进行了对比,发现结果符合较好,验证了计算程序的正确性和可靠性(见表2)。
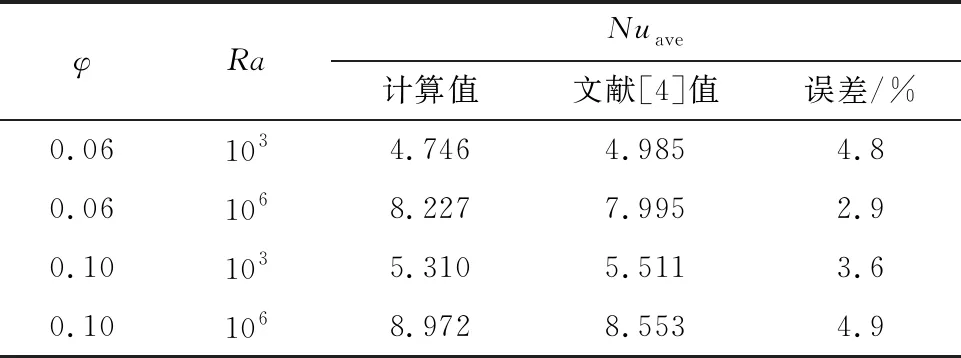
表2 Nuave计算值与文献[4]中相应值的比较
3 计算结果与讨论
数值计算中Ra数分别为104、105、106及107,纳米颗粒体积分数φ分别取值为0.025、0.05、0.075及0.1,腔体倾角的变化范围为0°、30°、60°和90°。
不同Ra数下腔体内φ=0.1的Cu-水纳米流体和纯水的最大流函数值Ψmax随腔体倾角γ的变化规律如图2所示,图2中虚线表示纯水的Ψmax随γ的变化曲线,而实线表示φ=0.1的Cu-水纳米流体的Ψmax随γ的变化曲线。由图2可知,当Ra=104时,腔体内Cu-水纳米流体和纯水的Ψmax随腔体倾角γ的变化曲线基本重合,而当Ra=105时,腔体内Cu-水纳米流体和纯水的Ψmax随腔体倾角γ变化曲线逐渐开始分开,且φ=0.1的Cu-水纳米流体的Ψmax值较纯水对应的Ψmax数值更大。同时从图2也可看出,当Ra=104~106时,腔体内Cu-水纳米流体及纯水的最大流函数值Ψmax均随腔体倾角γ变化不明显,当Ra数增大至107时,Ψmax随腔体倾角γ变化较明显。整体来说,当Ra=104~106时,腔体倾角对腔体内Cu-水纳米流体及纯水的流动强度的影响都不明显,而当Ra数增大至107时,腔体内Cu-水纳米流体和纯水的流动强度均随着腔体倾角的增大先增大后减小。出现上述现象的原因主要有:(1)当Ra数较小的时候由于浮升力较小,换热过程主要以导热为主,而随着Ra数进一步增加,流体浮升力越来越大,换热过程逐渐出现以对流为主的趋势,所以当Ra数较大时,会形成对流漩涡;(2)在E型腔体内,由于其腔体形状的特殊性,通过腔体内流场图分析发现,随着倾角的不断变化,腔体内会形成不同流动方向的冷、热对流漩涡,从而影响流体的流动强度。
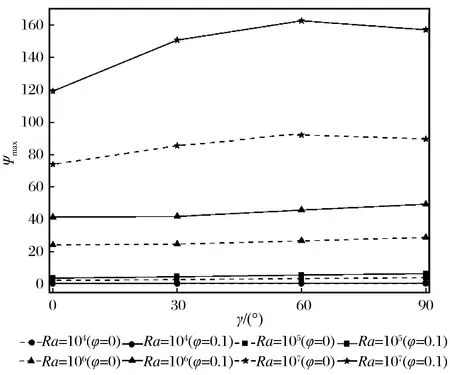
图2 不同Ra数下水和φ=0.1 Cu-水纳米流体的Ψmax随γ的变化Fig.2 Variation of Ψmax of water, and φ=0.1, Cu-water nanofluids with different Ra values
不同Ra数下腔体内φ=0.1的Cu-水纳米流体和纯水的平均努塞尔数Nuave随腔体倾角γ的变化规律如图3所示,图3中虚线表示纯水的Nuave随γ的变化曲线,而实线表示φ=0.1的Cu-水纳米流体的Nuave随γ的变化曲线。由图3可知,当Ra数较小(Ra=104、105)时,腔体内Cu-水纳米流体及纯水
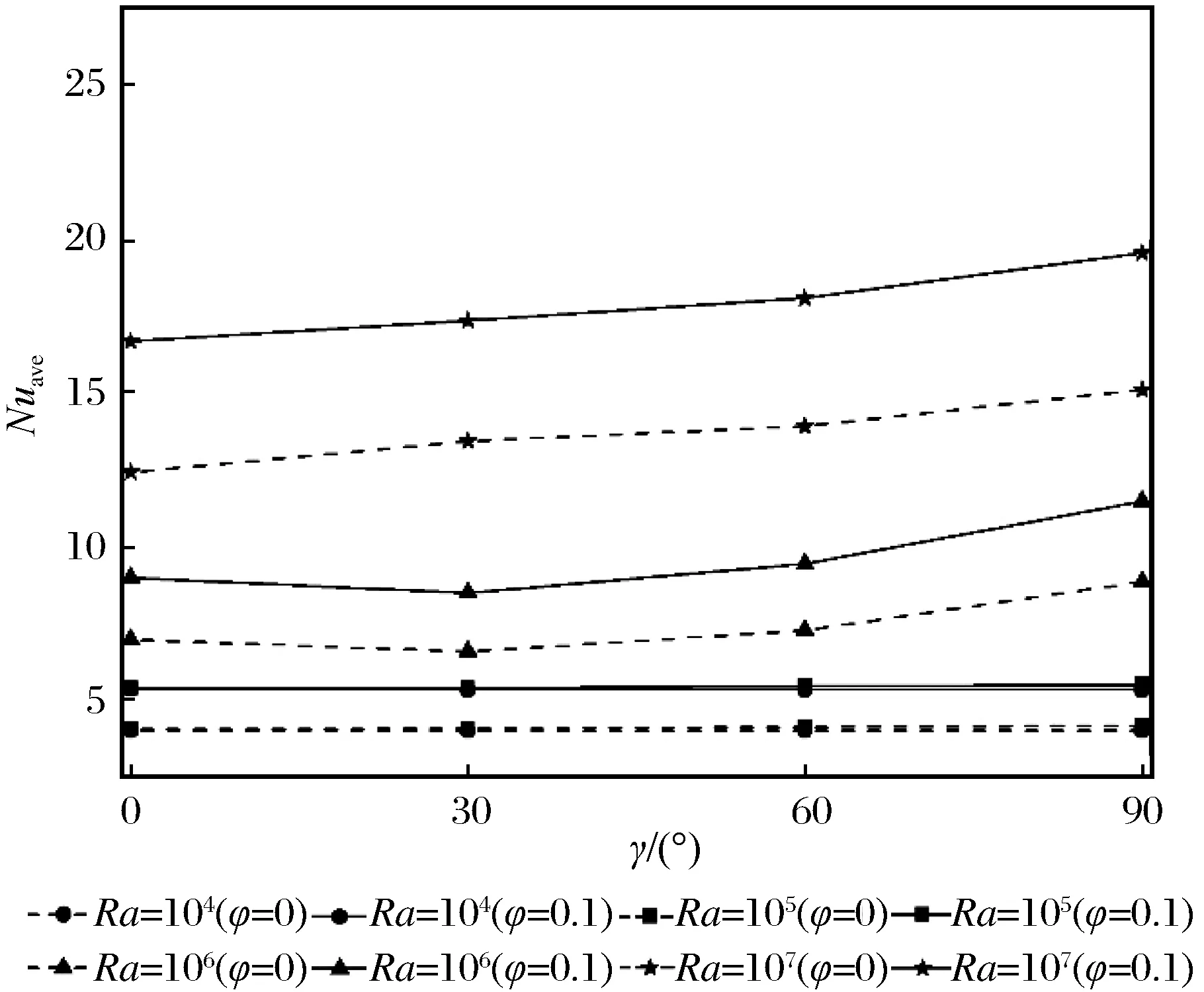
图3 不同Ra数下水和φ=0.1 Cu-水纳米流体的Nuave随γ的变化Fig.3 Variation of Nuave of water, and φ=0.1 Cu-water nanofluids with different Ra values
的Nuave均随腔体倾角γ变化不明显,当Ra数较大(Ra=106、107)时,Nuave随腔体倾角γ变化较明显。而且φ=0.1的Cu-水纳米流体对应的Nuave数值较纯水对应的Nuave数值更大。不仅如此,Ra数较大时对应的Nuave数值较Ra数较小时对应的Nuave数值更大。整体来说,当Ra数较小(104~105)时,腔体倾角对腔体内Cu-水纳米流体及纯水的换热效果影响都不明显,而当Ra数增大至107时,腔体内Cu-水纳米流体和纯水的换热效果均随着腔体倾角的增大而增大,且腔体内Cu-水纳米流体及纯水的换热效果均随着Ra数的增大而增强。原因同上所述。
当Ra数为107且纳米颗粒体积分数φ取值不同时,热壁面平均努塞尔数Nuave随倾角γ的变化规律如图4所示。从图4明显可以看出,φ值较大时对应的Nuave数值比φ值较小时对应的Nuave数值更大,且当φ值一定时Nuave均随着倾角的增大而增大,即当Ra数为107时,Nuave随着纳米颗粒体积分数φ和腔体倾角γ的增大均呈增大趋势。这一点也同时应证了图3的结论。
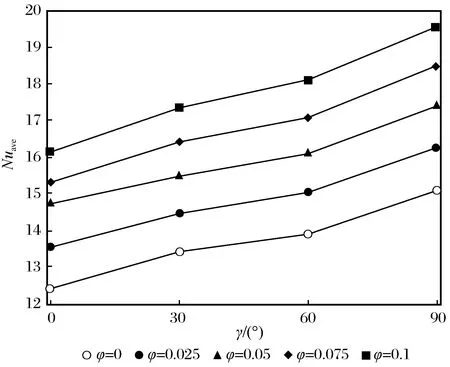
图4 Ra=107时不同φ下Nuave随γ的变化Fig.4 Variation of Nuave with γ with different φ when Ra=107
通过以上分析可知,基液中添加纳米颗粒会强化流体的换热效果。此处,为了衡量纳米颗粒体积分数φ=0.1的纳米流体比纯流体(纯水)条件下的传热效果强化程度,引入添加纳米颗粒增强传热的百分率%Enhancement(后文简写为%E),定义为
(15)
腔体倾角γ不同的情况下,添加φ=0.1的纳米颗粒增强传热的百分率%E随Ra数变化的分布如图5所示。由图5可知,当φ一定时,纳米颗粒体积分数强化传热百分率%E随Ra数的增大而减小,也就是说,通过添加纳米颗粒而强化传热的效果随着Ra数的增大而变弱,尤其是当Ra数由106增大至107时,通过添加纳米颗粒而强化传热的效果几乎趋于一个稳定值。
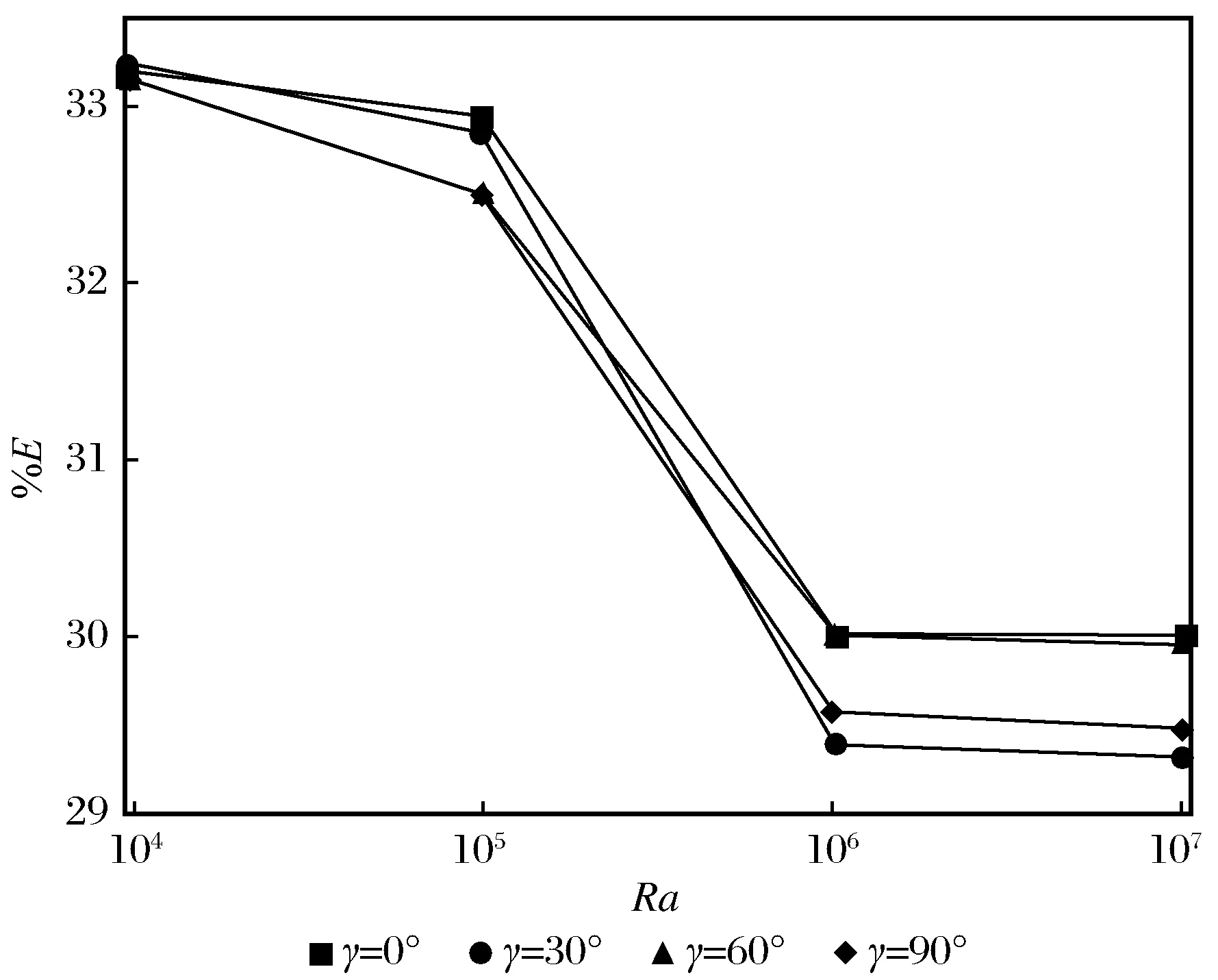
图5 不同γ下%E随Ra数的变化Fig.5 Variation of %E with Ra with different γ
4 结论
研究对E型倾斜腔体内Cu-水纳米流体自然对流换热进行了数值对比,主要分析了纳米颗粒体积分数φ、Ra数和腔体倾角γ对腔体内自然对流换热的影响,同时也计算得到了添加纳米颗粒增强传热的百分率%E。结果表明:在基液中添加Cu纳米颗粒时可强化腔体内Cu-水纳米流体自然对流换热效果及流体的流动强度,其换热效果和流动强度均随着φ的增大而增强;当φ一定时,腔体内Cu-水纳米流体自然对流换热强度随着Ra数的增大而增大;γ对换热结果的影响主要取决于Ra数的大小,当Ra数较小时,γ对换热结果的影响不明显,而当Ra数增大到107时,平均传热速率随γ的增大而增加。当φ一定时,纳米颗粒体积分数强化传热百分率%E随Ra数的增大而减小,说明通过添加纳米颗粒而强化传热的效果随着Ra数的增大而减弱。
