活用课本探究资源 提升探究活动实效①

朱胜强

(南京外国语学校 210008)

《普通高中数学课程标准(2017年版)》(以下简称《标准(2017年版)》)将数学建模活动与数学探究活动作为课程内容的四条主线之一，贯穿于必修、选择性必修和选修课程之中.与《普通高中数学课程标准(实验)》(以下简称《标准(实验)》)的要求相比，数学探究活动在课程中的重要性又有了新的提升，相应地对教师的要求也定会更高.课题的选择是有效开展探究活动的关键，而如何获得适合学生探究的课题也是教师的困扰所在.

与《标准(实验)》配套的教材中都设计了一定数量的探究问题或背景材料，这是开展探究活动的重要参考.在具体的教学实践中，教学活动往往受诸多因素影响，因此课本配备的探究资源未必总能很好地契合教学需求，这势必影响探究活动的实效.面对这一问题，笔者尝试了对问题进行再设计，灵活运用课本探究资源，使之能更好地服务于数学探究活动.下面谈一点做法体会，供大家参考.

1 课本探究素材简析

如图1(1)，一个四面体木块ABCD，在△ABC的面内有一点P，要经过点P在平面ABC内画一条直线l，使l⊥AD，怎样画？写出作法，并给予证明.

该问题背景比较直观，易与学生生活实际建立起联系.学生童年时期一般都有玩积木的体验，立几模型与直观图相比，更容易引发学生对空间几何关系的感知与想象.因而，学生对这样的问题比较感兴趣，愿意自觉地用所学立体几何知识进行思考.但问题涉及的立体几何知识较为基础，且应用方式不很复杂，因此，对于生源质量良好的学校学生来说，探究的难度不会很大.

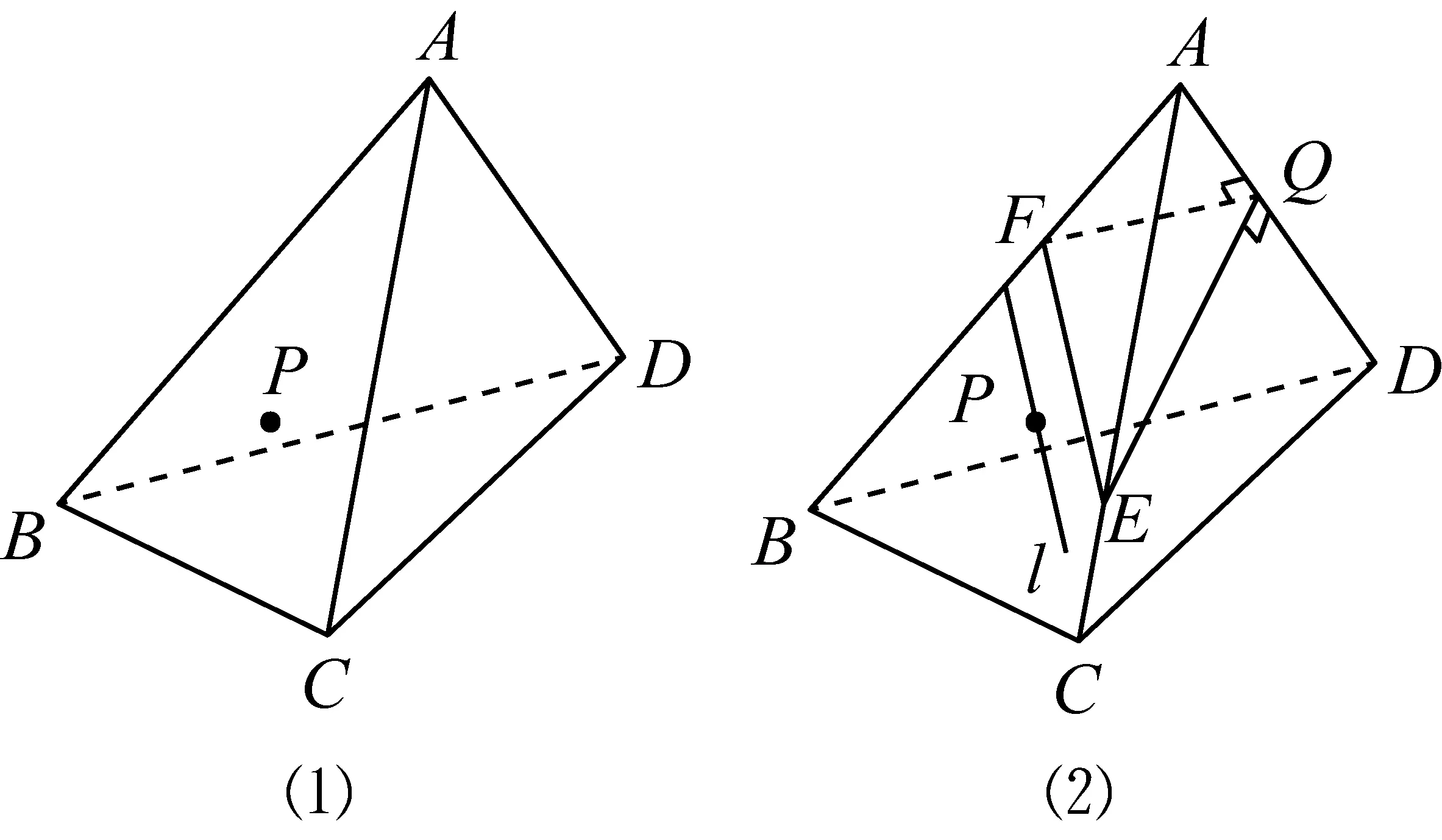
图1

下面是配套的教学参考书提供的解答：

如图1(1)，在AD上任取异于A，D的一点Q，过点Q分别在平面ACD和平面ABD内作QE⊥AD，QF⊥AD，并分别交AC，AB于E，F两点.连结EF，过点P在平面ABC内作直线l，使l∥EF，则l即为所求直线.

已有的教学实践表明，学生想到的方案与上述答案大体相仿.由于问题的探究过程没遇太多曲折，所以探索后学生总觉得该问题作为“探究拓展”题少了点探究的味道.

教材的编写须顾及使用者的整体情况，所以不能苛求教材设计总能适合任一群体的学生.作为教学活动主导者的教师在如何用好教材上则应发挥自己的作用.

2 对课本问题的再设计

为使课本探究资源能更好地符合教学需求，可考虑对相关问题进行再设计.如何再设计呢?《标准(2017年版)解读》关于数学建模和数学探究选题的几个注意点值得参考:

(1)有研究价值和现实可行性.考虑到学生年龄特征、知识水平和实际能力；

(2)尽可能结合学生的生活实际和学生们关注兴趣点；

(3)求解过程有利于学生理解数学，有利于综合利用所学知识，有利于学生个性和不同特长的发挥，有利于培养学生的合作精神和创新意识；

(4)可以给学生一个学习和体验“做研究”的过程，帮助学生积累数学活动经验.

因此，本题的再设计应保留能引发学生兴趣的因素；考虑到学生数学基础较好的现状，及让学生有机会综合运用立几知识，可让问题在原有基础上增加一定的难度；为让不同层次的学生都能有所收获，可让问题有一定的梯度；为让学生获得较完整的探究体验，可增加动手操作的环节.

为此，再设计后的问题仍以“在四面体模型指定面中画某棱垂线”的形式出现；针对图1(1)所示四面体ABCD中，∠BAD与∠CAD是否为锐角，将问题分为不同的类别，既提高挑战性，又凸显层次差异；考虑到活动过程的完整性，设计了模型制作环节.再设计后的问题如下：

分别制作如下三类不同的四面体模型ABCD.又P为面ABC内的一点P，试经过点P在面ABC内画一条直线l，使l⊥AD，怎样画？写出作法，并给予证明.

第一类:∠BAD与∠CAD均为锐角;

第二类:∠BAD与∠CAD均为钝角;

第三类:∠BAD与∠CAD中一个是锐角,另一个是钝角.

为尽可能保证探究效果，还给出了探究的一些建议与要求：可按自愿的原则组成活动小组，每组都需针对三类不同的模型进行制作与作图研究；四面体模型可用硬纸板、橡皮泥或泡沫塑料制作，但不宜用铁丝等制成四面体的框架；在模型上作图时，仅限用尺规法，不得借助其它的测量仪器与工具.

3 探究成果展示

经过一段时间的自主探究后，探究活动顺利结束.教师组织学生以适当的形式进行成果展示，并进行评价.下面侧重介绍学生获得的主要探究成果.

3.1 第一类模型的新作法

对于第一类四面体模型，学生想到的除了与教学参考书相同的方法外，还有学生想到了依据三垂线定理来作图.其思路是这样:先作出AD在面ABC内的射影，然后过点P在面ABC内作射影的垂线.

对于第一类四面体，如何作得AD在平面ABC内的射影呢?

因为∠BAD与∠CAD均为锐角，所以，在棱AD上取异于A，D的一点Q，过点Q分别在面ACD和平面ABD内，作QE⊥AC，QF⊥AB，并分别交AC，AB于E，F两点.

在面ABC内，作EG⊥AC，FG⊥AB.

易知，AC⊥平面QEG，所以，平面QEG⊥平面ABC；

同理可知，平面QFG⊥平面ABC. 注意到，平面QEG∩平面QFG=QG.所以，AC⊥QG，AB⊥QG，所以,QG⊥平面ABC.

因此，G是Q在平面ABC内的射影，即AG是AD在平面ABC内的射影(如图2). 这样,只要过点P作直线AG的垂线，便得所求直线l.

图2

上述探究中，学生发现并提出如下命题：

已知平面α，β，γ，α⊥γ，β⊥γ，α∩β=l，则l⊥γ.

3.2 第二类模型的探究

对于第二类模型，因为∠BAD与∠CAD均为钝角，若在棱AD上任取异于A，D的一点Q，过Q在平面ABD内作AD的垂线，应与棱BD相交，记交点为F；同理，过Q在平面ACD内作AD的垂线，应与棱CD相交，记交点为E.由于E，F两点不在AC与AD上，所以教学参考书提供的方法不再适用(如图3).

图3

如果过Q点在平面ACD内作AC的垂线，因为∠CAD是钝角，所以垂足在CA的延长线上.因此，试图作出AD在平面ABC内射影的方法似乎也行不通了，只得另寻他法.

图3中由QE，QF两条相交直线确定的平面是与AD垂直的平面，平面QEF内任一条直线都与AD垂直.如果将平面QEF平移至与平面ABC相交，则交线必与AD垂直.

为此，在AC上取一点G，过G在平面ACD内作QE的平行线交CD于H.过H在平面BCD内作EF的平行线.

若平行线与BD相交，记交点为K，过K在平面ABD内作QF的平行线交AB于L.连结LG,则LG便是平面ABC内与AD垂直的直线(如图4(1)).

若平行线与BC相交，记交点为K，连结KG，则KG便是平面ABC内与AD垂直的直线(如图4(2)).

图4

上述探究中，学生发现并提出如下立几命题：

如图5，已知平面α∥β，A∈α，A∈a，b⊂β，a∥b，则a⊂α.

真的无法作出AD在面ABC内的射影吗？有人做出了成功的尝试.

图5

为直观起见，这里将图4中的几何体的面ABC朝下放置(如图6).在AD上适当位置取一点Q，过Q在平面ACD内作AC的平行线交CD于E；在平面ABD内，过Q作AB的平行线交BD于F.其中∠AQE与∠AQF均为锐角.

图6

过A作QE的垂线，交QE于G；过A作QF的垂线，交QF于H.过G作AD平行线交AC于K，过H作AD平行线交AB于L.在平面ABC内，作KM⊥AC，作LM⊥AB，则AM便是直线AD在平面ABC内的射影.

事实上，在图6中有一个以AKML为底面，以AQ为侧棱的四棱柱.不妨假设平面QGH内，过G垂直于QG的直线与过H垂直于QH的直线的交点为N，该四棱柱便是四棱柱AKML-QGNH(如图7).

图7

上述探究中，学生发现并提出如下立几命题：

在四棱柱AKML-QGNH中，已知AG⊥QG，AH⊥QH，KM⊥AK，LM⊥AL，则平面AQMN⊥平面AKML.

3.3 第三类模型的探究

此类四面体模型中，∠BAD与∠CAD一个为锐角，一个为钝角，不妨设∠CAD为锐角，∠BAD为钝角.此时，若在棱AD上任取异于A，D的一点Q,在面ABD内，过Q作AD的垂线，则必与棱BD交于点F.在面ACD内，过Q作AD的垂线，则垂线可能与棱CD相交，也可能与棱AC相交.

若所作垂线与棱CD相交，便可得到过Q与AD垂直的截面.此时，仿照第二类四面体解决问题的办法，平移AD的垂面便可解决问题.

若所作垂线与棱AC相交，记交点为E. 则平面QEF与平面ABC的交线便是平面ABC内与AD垂直的直线.

如果作图不局限于模型表面，还是有办法的.许多立体几何教材中都有类似于这样的命题：

三个平面两两相交，有三条交线，则这三条交线交于一点或互相平行.

依据给定公理不难证得此命题.该命题可用来确定交线.

考虑三个两两相交的平面，即平面ABC，平面ABD，平面QEF.其中平面ABC∩平面ABD=BA，平面ABD∩平面EFQ=FQ.E是平面ABC与平面QEF的一个公共点(如图8).

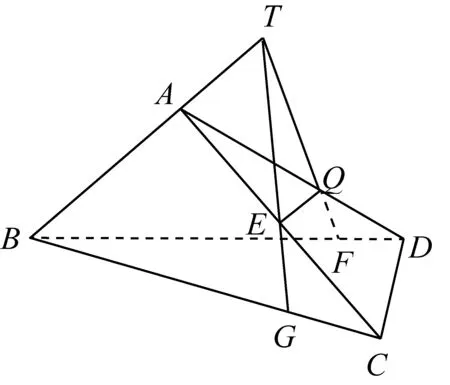
图8

若FQ与AB相交，记交点为T，则平面ABC∩平面QEF=ET.

设ET与BC的交点为G，则平面EFQ∩平面ABC=EG.

若FQ∥AB，这时平面EFQ与平面ABC的交线也必与AB平行.因此，过E作AB的平行线，可得平面EFQ与面ABC的交线.

当然，这种作法不是最终解决问题的方法.应考虑到在四面体模型上作图的局限性，是否可以对这种作法进行改进呢？

考虑以B为放缩中心，将四面体ABCD适当缩小，缩小到图8中所画的这些线都可以在模型表面作出.下面仅以FQ与AB相交为例加以说明.

连结BE交A1C1于点E1，连结AE1并延长交BC于G(如图9).

图9

易知平面AF1G∥平面QEF.所以AG⊥AD，因此AG即为平面ABC内与AD垂直的直线.

这一作法本质上是通过放缩变换平移平面QEF，得到AD的垂面与平面ABC的交线.

上述探究中，学生发现并提出如下命题：

已知三棱锥S-ABC，A′，B′，C′是侧棱SA，SB，SC上的点.若SA′∶SA=SB′∶SB=SC′∶SC，则平面ABC∥平面A′B′C′(如图10).

图10

4 探究问题再设计后的思考

《标准(实验)》指出，数学探究即数学探究性课题学习，是指学生围绕某个数学问题，自主探究学习的过程.因此，数学探究是以一类问题为载体、以学生自主参与为主的学习活动.所以活动组织和设计的核心是“问题”或“问题串”.寻找好的问题、把求解问题的过程设计成学生便于理解、参与的形式，自然成为数学探究设计的首要工作.

作为探究载体的“问题”来源可能多样，但教材、教学参考书等现有的与日常教学相伴的资源却是不应忽视的.这就要求教师在教学中要有“问题”意识，合理用好问题资源.通过自己的再度加工，将课本的探究资源设计成学生感兴趣，与能力水平相适应，能够获得丰富体验的“好问题”.事实上，这些取自于日常教学的问题资源，更有利于调动学生的学习积极性和参与度，更能提升探究活动的实效.

多数情况下信手得来的“问题”并非最理想的探究素材，需要教师根据实际情况进行雕琢.但这项工作与教学例题或考试试题的设计又不同，要考虑学生自主探索的可行性与探索之后可能的收获，这对教师自然是一种考验.一个理想的探究“问题”也不是仅凭教师头脑中的想像就自然形成的，往往还需经教学实践的反复检验.所以，教师要更好地适应新课程标准的要求，就应努力成为数学探究课题的创造者，有比较开阔的数学视野，了解与中学数学知识有关的扩展知识和内在的数学思想，认真思考其中一些问题，加深对数学的理解，提高数学能力，为指导学生一进行数学探究做好充分准备，并在教学实践中不断积累指导学生进行数学探究的资源.这样，开展数学探究活动时其效果便有了基本保障.