基于两种方法的铁路隧道弃渣场抗滑稳定性分析

郑良静

(中铁二十一局集团有限公司 甘肃兰州 730070)

1 前言

隧道弃渣场一般由开挖隧道所排出的松散土体、碎石等物质组成，具有非饱和、欠密实、多孔隙等结构特点；强度较低，容易产生滑坡等地质灾害，对其下方建筑物、公用设施以及居民的生命财产安全等都存在着巨大威胁[1]。弃渣堆积体稳定性主要受堆积体几何形态、物理力学性质和下伏基岩产状及物理力学性质、地表水及地下水等因素影响。稳定分析方法主要有工程地质法、传统极限分析法以及数值极限分析法[2]。

通常边坡稳定的安全系数与滑动面位置关系密切[3]，张昊[4]等以均质边坡为例采用强度折减法计算分析了边坡稳定过程中安全系数和滑动面之间的关系。李建朋[5]等基于临界状态速度场的分析，提出了一种新的边坡临界状态滑动面确定方法。

隧道弃渣堆积体多孔多相不均匀，结构松散欠密实，传统方法在确定破坏面形态方面存在困难[6]。刘建伟[7]等通过采集测定坡面不同位置处弃渣容重、含水量、饱和导水率、饱和含水量、砂粒含量、碎石含量等物理指标和直剪试验，分析了弃渣场边坡稳定性特征。杨华清[8]以云南省华丽高速26号合同段弃渣场为例研究了粒组级配、最终堆积形态及弃渣场稳定的关系。数值计算方面，田永铸[9]针对中南部铁路通道沿线某一黄土隧道弃渣场，通过现场勘查及已有相关资料，结合室内外土工试验，运用理论分析方法，对该弃渣场的稳定性进行计算与分析。毛雪松[10]等以某新近堆积弃渣场为例，采用非饱和渗流研究方法，基于GeoStudio软件中的SEEP/W和SLOPE/W模块对其渗流场及不同工况下的稳定性进行分析。孙朝燚[11]等通过现场地质调查和区域划分，借助基于强度折减法的有限元软件分析弃渣场边坡稳定性和潜在破坏机制，以此研究弃渣场走向夹角对其潜在破坏机制的影响。本文以新建铁路敦格线阔克萨隧道弃渣场为例，介绍一种较为实用且稳妥的计算弃渣场抗滑稳定安全系数的方法。

2 工程概况

新建铁路敦格线阔克萨隧道段区域隶属于甘肃省阿克塞县，隧道洞身穿过当金山脉。阔克萨隧道弃渣场位于阔克萨隧道出口DIK191＋600右侧荒沟内。弃渣场设计弃渣量约4.87万m3，占荒沟9.57亩。弃渣场前缘高度约为8 m，坡度约45°，弃渣堆坡顶平台宽度约为43 m。坡脚采用挡墙防护，挡墙高8 m，基础埋深2 m。挡墙顶部设置一个宽为10 m的平台，弃渣堆边坡前缘无人员活动场所和设施，至2019年边坡已稳定存在五年。

弃渣场平均海拔约2 858 m，最高海拔2 888 m。弃渣场所在区域为中温带干旱气候区，降水量小，蒸发量大，冬冷夏热，空气干燥。年平均气温3.1℃，年平均降水量127 mm，年平均蒸发量3 297.9 mm。土壤最大冻结深度235 cm。弃渣场范围未见地表水，偶见有积雪融水，隧道洞身及附近未见地下水出露。地下水类型为第四系潜水及基岩裂隙水，补给主要靠大气降水及地表径流，排泄以蒸发和地下径流为主。

阔克萨隧道弃渣以断层角砾、碎裂岩为主。断层角砾呈灰白色、青灰色，尖棱状～棱角状，成分以石英片岩为主，粒径2～20 mm的含量约为50%，20～60 mm的占5% ～15%，粉土、砂土充填，局部可见轻微泥砂质胶结，角砾手可捏碎，夹断层泥，稍湿，密实；碎裂岩呈棕红色，原岩为泥岩夹砾岩，成分以黏土矿物为主，洞身段碎裂岩为灰黑色、青灰色，表面局部呈锈黄色，原岩为石英片岩，成分以石英、云母等为主，岩质受构造影响破碎不均，局部呈巨块状，大部呈碎石状、角砾状。

弃渣场地基为粉土，灰黄色，土质不均，含少量砾石，表层含植物根系，稍湿。

3 弃渣场边坡稳定性分析

弃渣场抗滑稳定性计算一般采用瑞典圆弧法，对于均质渣体推荐使用简化毕肖普法，对于有软弱夹层的渣场，宜采用摩根斯顿-普赖斯(M-P)法计算[12]。本弃渣场弃渣组分多元，为非均质渣体。为保证计算分析的可靠性，首先采用强度折减法进行边坡稳定性分析，确定临界滑动面形态，然后采用传统极限平衡法中的M-P法计算典型剖面的安全系数，并将二者计算结果进行比较。

3.1 计算工况

本弃渣场场地所在位置处于Ⅵ度烈度区，依据规范不需要考虑地震对弃渣场稳定性的影响。同时本地区属于典型的干旱地区(年降雨量不足200 mm)，且浅层无地下水分布，也无需考虑渗流工况或降雨工况下的边坡稳定性。因此，计算工况仅需考虑采用自然状态下岩土体物理力学参数分析弃渣场边坡稳定性。

3.2 计算坡面选取

根据现场实地测量，形成弃土堆坡面三维地形图，并选取坡度最大截面为稳定性分析的计算剖面。剖面尺寸见图1。

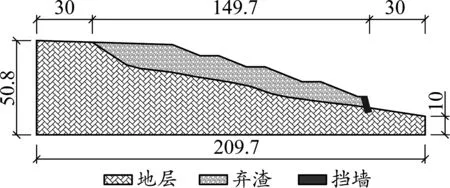
图1 计算剖面(单位:m)

阔克萨隧道弃渣场实际弃渣量约5万m3，最大堆渣高度约38 m，渣场失事对主体工程或环境造成的危害程度较轻，判别该弃渣场为4级弃渣场，计算参数如表1所示。

表1 岩土体及挡墙物理力学参数

3.3 强度折减法计算模型及分析结果

计算模型如图2所示，整个模型共划分4 996个单元，其中地层3 615个单元，弃渣堆1 352个单元，挡墙29个单元，均采用平面应变CPE4单元。土体和挡墙均采用摩尔-库伦模型，为防止滑动面穿过挡墙，挡墙混凝土材料的黏聚力和内摩擦角取较大数值。弃渣堆与地层边界采用非光滑面-面接触，弃渣堆与挡墙边界采用Tie连接，地层与挡墙部分边界采用非光滑面-面接触，部分采用Tie连接。外部边界条件如图2所示。

塑性变形云图见图3。可以看出，当强度折减系数为1.504时，挡墙处开始出现较大塑性应变，整个挡墙在墙后边坡的挤压作用下发生绕墙踵的转动位移，导致墙后及墙趾处塑性变形较大；当强度折减系数增大到1.642时，塑性区范围进一步扩大，滑动面尚未形成，但可见其绕过挡墙根部，由墙踵出发，逐渐向墙后弃渣堆积体内部发展，如图4所示；当强度折减系数进一步增大到1.678时，塑性区扩展到弃渣堆积体第一级平台顶部，从而在渣堆内部形成了一条贯通的滑动面，如图5a所示。

图2 有限元计算模型

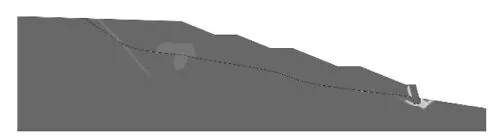
图3 塑性应变云图(折减系数＝1.504)

图4 塑性应变云图(折减系数＝1.642)

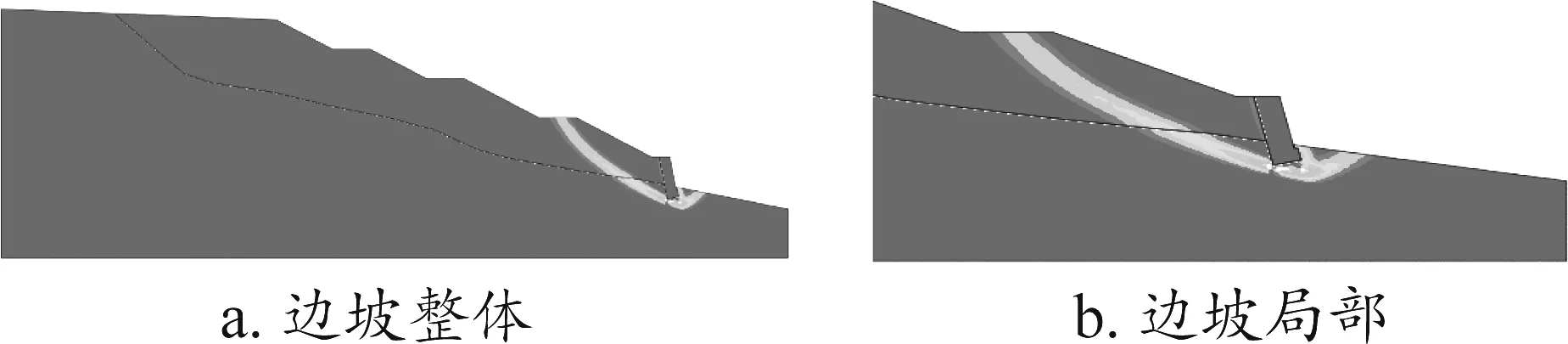
图5 塑性应变云图(折减系数＝1.678)

由图5b可见，挡墙前侧、墙蹱处以及墙背土体均出现塑性区，且墙背塑性区呈倒三角形，表明挡墙既有平动位移也发生了转动位移。渣堆体下部滑动明显，越往上，变形逐渐减小。

计算结果表明，当折减系数为1.642时(见图6)，挡墙顶部水平位移出现突增，即强度折减系数取为1.642时，边坡处于临界平衡状态。表明弃渣场边坡具有一定的强度储备。

图6 挡墙顶部水平位移(U1)随折减系数的变化

3.4 极限平衡法计算模型及分析结果

基于强度折减的有限元法结合弹性数值分析进行边坡稳定性评估，具有较高精度，但数值分析不能获得岩土的破坏状态与破坏面，因而无法求出极限荷载与稳定安全系数[12]。采用传统极限平衡法计算出临界滑动面的稳定安全系数，但是确定具有最小安全系数临界滑动面的位置是极限平衡法的关键。临界滑动面的位置及形态与地层分布、渣堆体及地层的物理力学性质等诸多因素有关，很难通过搜索确定可信的临界滑动面。如果将基于强度折减的数值法与基于极限平衡的传统分析法结合起来，就可以确定出破坏面，也可以求出稳定安全系数。

传统的极限平衡法计算模型采用相同的物理力学参数和几何尺寸，模型如图7所示。根据强度折减法分析的破坏面形态和位置，在极限平衡法中采用指定滑动面入口和出口的方式搜索临界滑动面，滑动面为圆弧面，条间力函数采用半正弦函数，分析结果安全系数为1.777。临界滑动面形态见图8，可见与强度折减法计算结果大体相近。根据规范，4级弃渣场正常运用抗滑稳定安全系数须大于1.2，因此可判定该边坡抗滑稳定性满足规范要求。

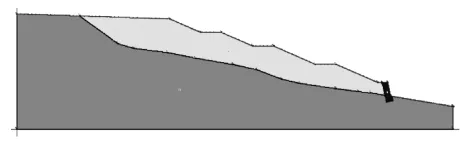
图7 极限平衡法计算模型

图8 临界滑动面形态

采用M-P法收敛情况如图9所示。M-P法通过引入系数λ和条间力函数建立条间竖向力和水平力之间的约束关系，使得静力平衡方程完备。当λ＝0时，M-P法力矩平衡退化为简化Bishop法(对应的安全系数为1.774)，力平衡退化为简化Janbu法(对应的安全系数为1.646)。

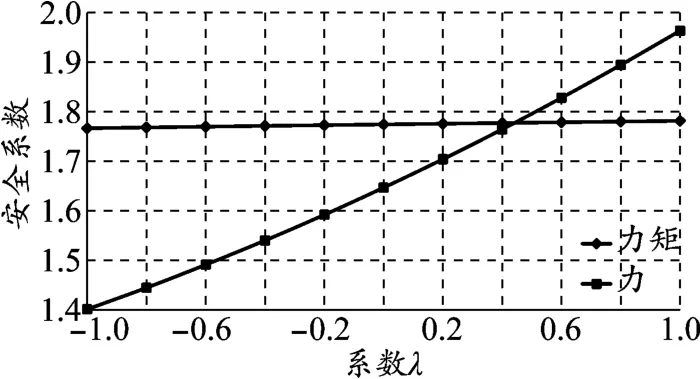
图9 安全系数随λ变化情况

4 结束语

综上所述，规范推荐采用传统极限分析法求解弃渣场稳定安全系数，但由于弃渣堆积体通常成分复杂，传统方法并不能完全适应，特别是在临界滑动面的位置和形态确定方面存在困难。因此对于弃渣场边坡抗滑稳定问题，建议首先应用基于强度折减法的有限元分析初步确定破坏面形态，然后根据破坏面的形态利用传统方法求解稳定安全系数。